If two particle are projected as shown then find i.e.,

(i) Particle collide or not.
(ii) If collide, then find collision time

Video Solution

Text Solution

Verified by Experts

$tan θ = \frac{10}{10 \sqrt{3}} = \frac{1}{\sqrt{3}}$
$θ = 30^{\circ}$
$θ = {tan}^{- 1} = (\frac{u_{A B_{y}}}{u_{A B_{x}}}) = {tan}^{- 1} (\frac{5 \sqrt{3}}{15}) = 30^{\circ}$
Here $u_{A B_{y}} = u_{A_{y}} - u_{B_{y}} = 0 - (- 10 {sin 60}^{\circ}) = 5 \sqrt{3} m / s$
$u_{A B_{x}} = u_{A_{x}} - u_{B_{x}} = 10 - (- 10 {cos 60}^{\circ}) = 15 m / s$
So $u_{A B}$ is along AB particle will collide.
$u_{A B} = \sqrt{15^{2} + {(5 \sqrt{3})}^{2}} = 10 \sqrt{3} m / s$
$t = \frac{s_{A B}}{u_{A B}} = \frac{\sqrt{10^{2} + {(10 \sqrt{3})}^{2}}}{10 \sqrt{3}} = \frac{20}{10 \sqrt{3}}$
$t = \frac{2}{\sqrt{3}}$ sec.

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two particles are projected simultaneously from the level ground as shown figure. They may collide after a time :

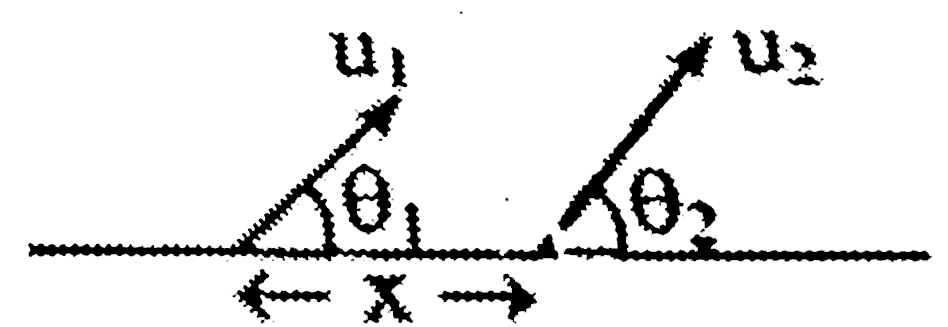A $\frac{x {sin θ}_{2}}{u_{1}}$
B $\frac{x {cos θ}_{2}}{u_{2}}$
C $\frac{x {sin θ}_{2}}{u_{1} sin (θ_{2} - θ_{1})}$
D $\frac{x {sin θ}_{1}}{u_{2} sin (θ_{2} - θ_{1})}$
Question 2 - Select One
A particle is projected from the ground with speed u at angle $60^{\circ}$ from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
A $\frac{3 \sqrt{6} u^{2}}{8 g}$
B $\frac{3 \sqrt{3} u^{2}}{8 g}$
C $\frac{u^{2}}{8 g}$
D $\frac{\sqrt{3} u^{2}}{g}$

ALLEN-KINEMATICS-Integer Type Question

Home
Ask Doubt
Profile