The left end of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.
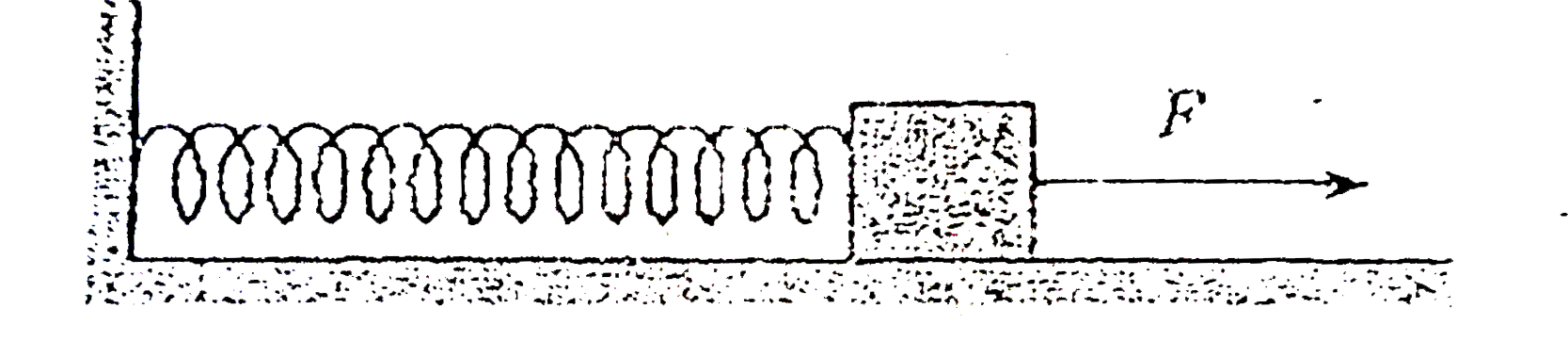
What is the maximum speed of the block in the ensuing motion after the force F is removed?
√Fxm
√Fx2m
√2Fxm
x√Fm
The correct Answer is:A
kx=F and 12kx2=12mv2⇒v=√Fxm
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionIn Fig. three identical massless springs are kept horizontal. The left end of the first is tied to a wall. The left end of the second spring is tied to a block of mass m placed on rough ground and the ,eft end of the third spring is tied to a block of mass m placed frictionless ground. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extensions in these springs are x1, x2 and x3, respectively. Find the relationship between x1, x2, and x3

View Solution
Knowledge Check
In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
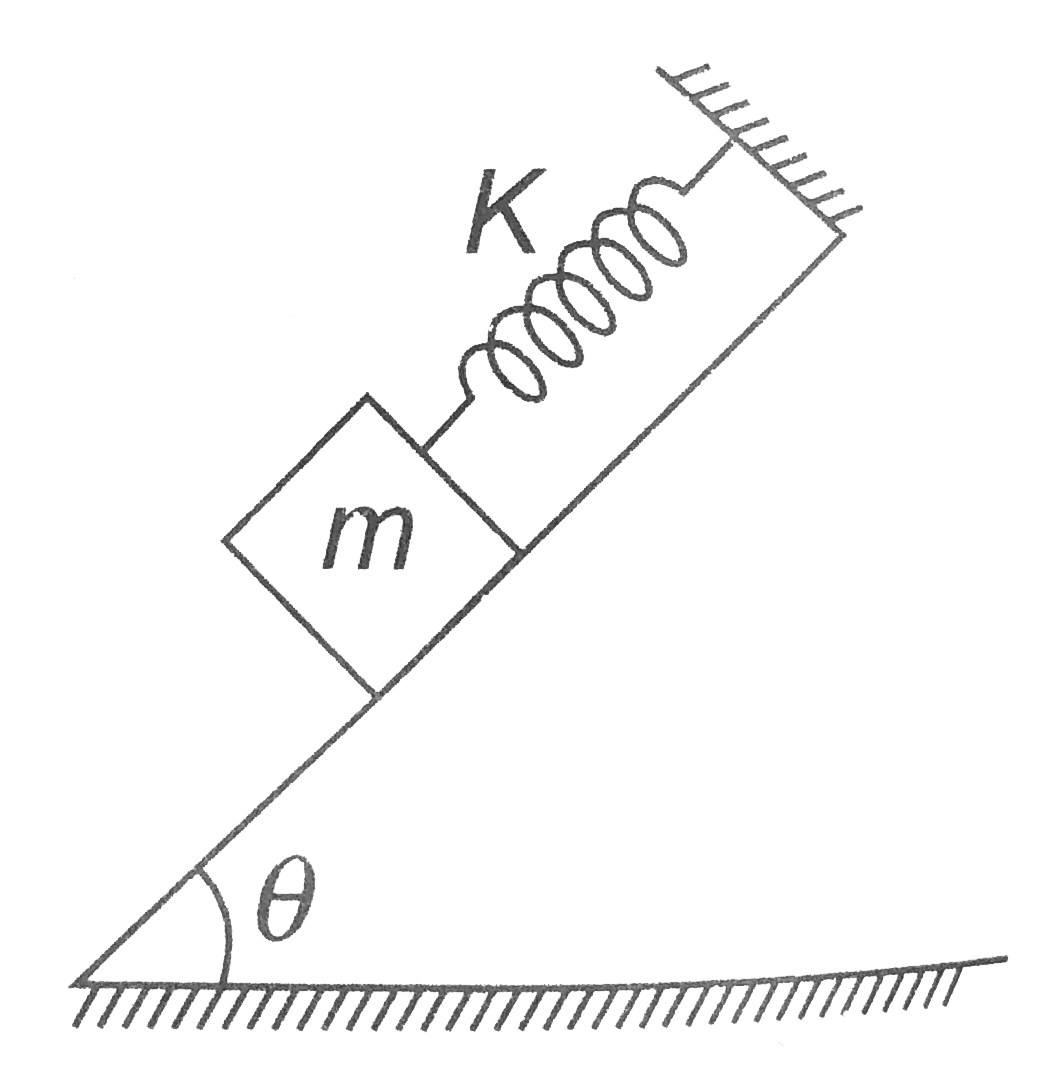 A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mkOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
AThe spring was initially compessed by a distance x and was finally in its natural length .BIt was initially stretched by a distance x and finally was in its natural length.CIt was initially natural length and finally in a compressed position.DIt was initially in its natural length and finally in a stretched position.Two springs are in a series combination and are attached to a block of mass 'm' which is in equilibrium. The spring constants and extension in the springs are as shown in the figure. Then the force exerted by the spring on the block is :
 Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of these
Ak1k2k1+k2(x1+x2)Bk1x1+k2x2Ck1x1DNone of these
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionA spring of force constant 24N/m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
View SolutionA force F is applied on a block of mass M. The block is displaced through a distance d in the direction of the force. What is the work done by the force on the block? Does the internal energy change because of this work?
View SolutionTwo blocks of masses m and M connected by a spring are placed on frictionless horizontal ground. When the spring is relaxed, a constant force F is applied as shown. Find maximum extension of the spring during subsequent motion.
View Solution
