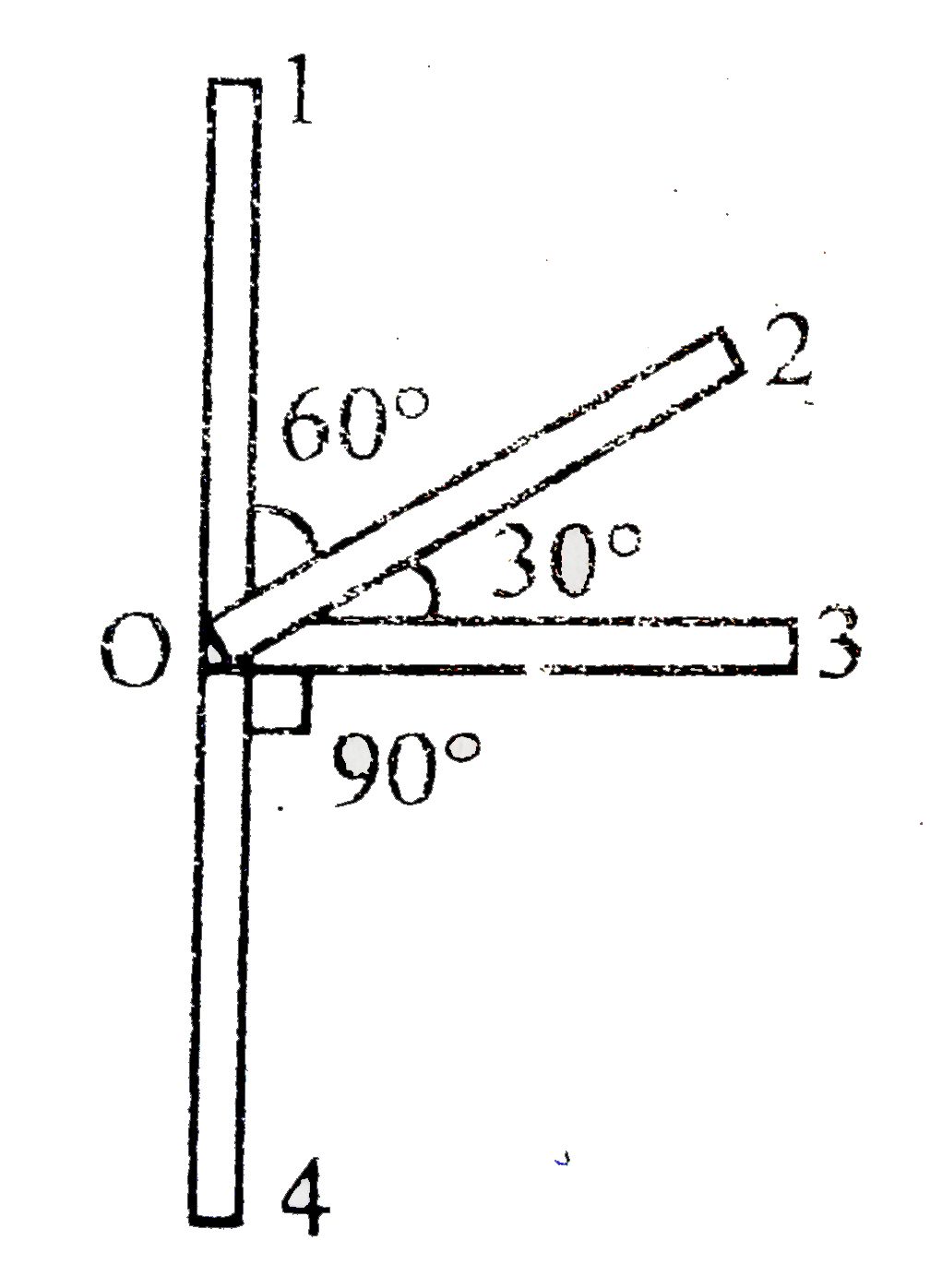
A thin rod free to rotate about a horizontal axis through one end O is initially is unstable equilibrium position 1 and falls due to gravity on being displaced infinetsimally. In positions 2,3 and 4 it makes 60∘,90∘ and 180∘ with the upward vertical. Let ω2,ω3 and ω4 be angular velocities of the rod in these positions then
The correct Answer is:BD
mg(l2−l2sin30∘)=12Iω22
mgl2=12Iω23
mgl=12Iω24
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
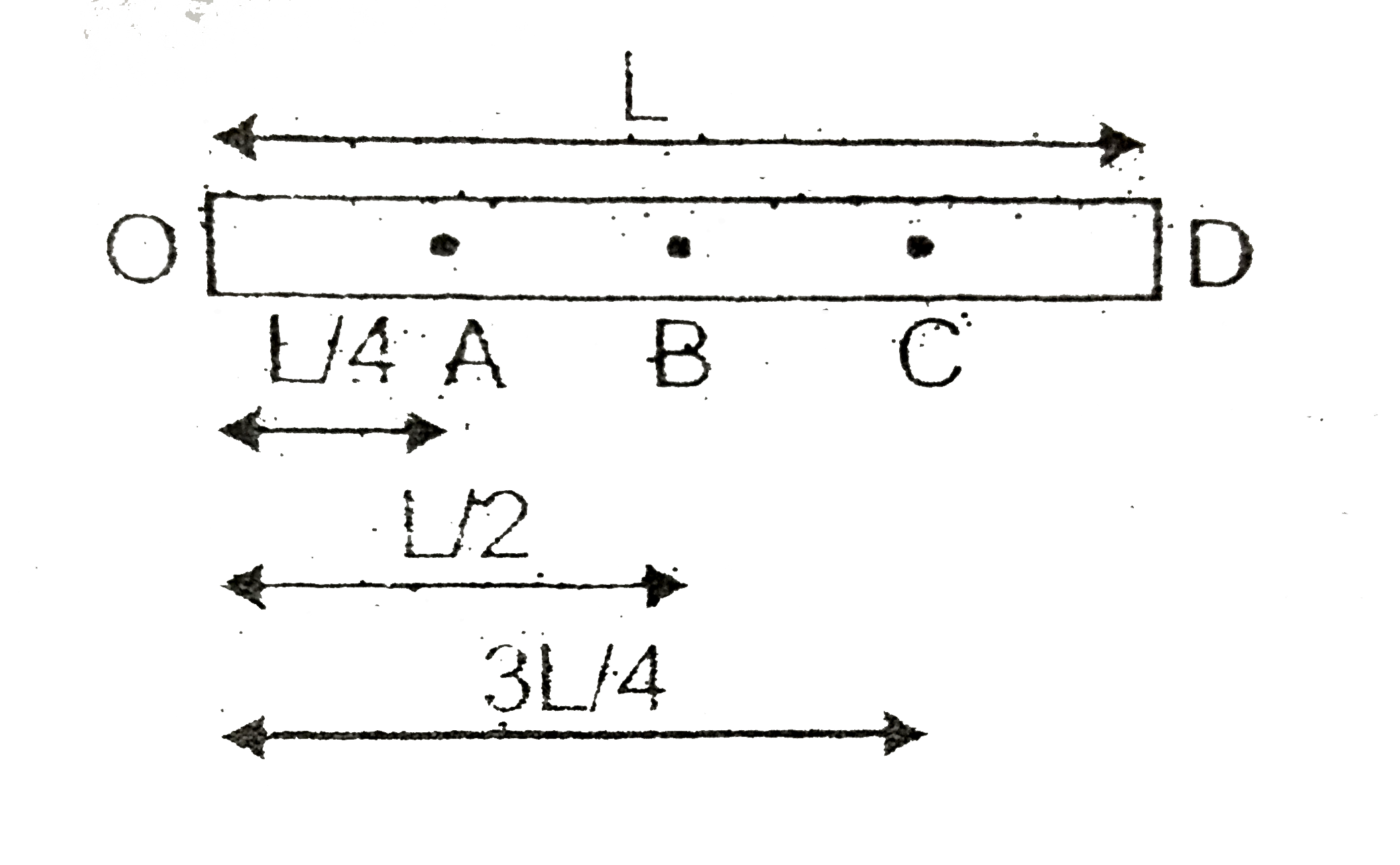
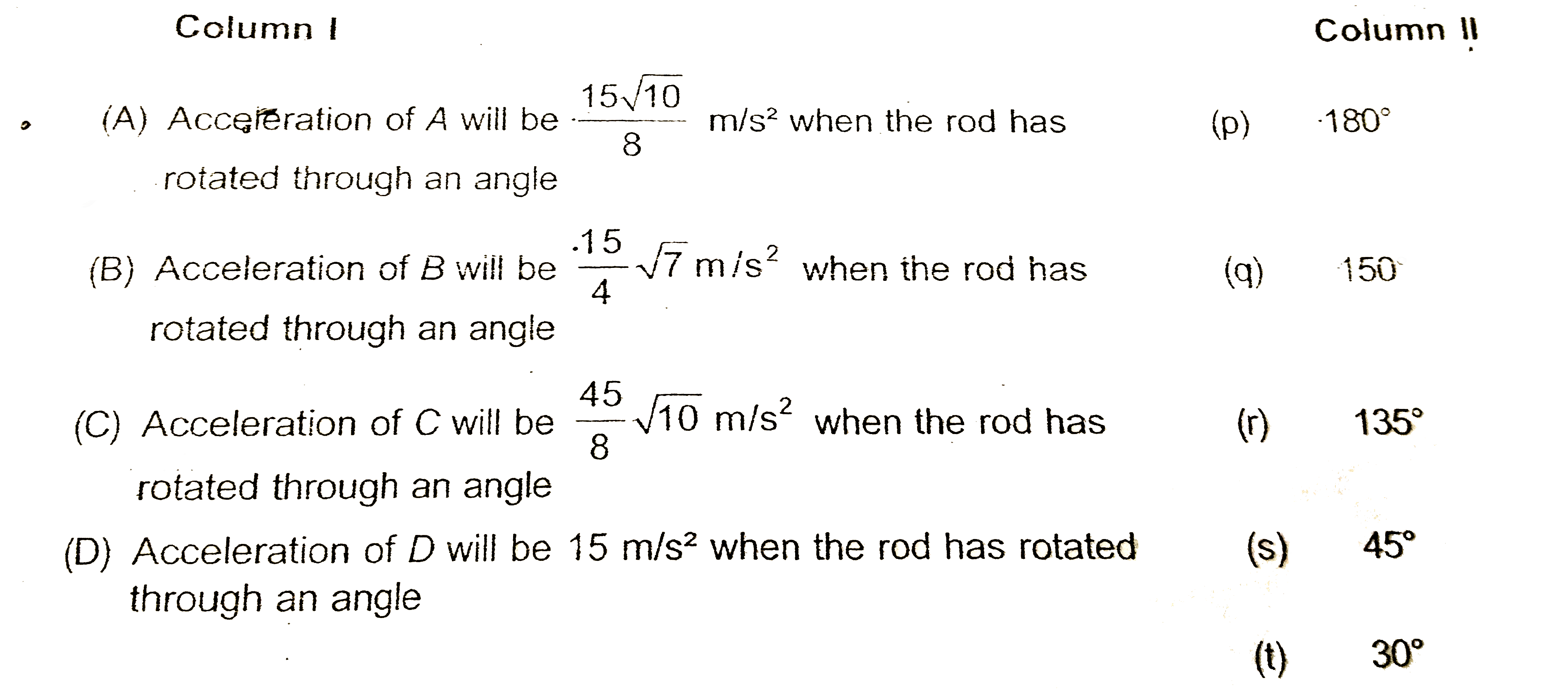
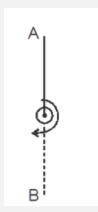
View SolutionA uniform rod is rotating about a horizontal axis as shown. The rod is hinged at one of the ends. The rod is released from a vertical position by slightly pushing it. As the rod moves from A to B
View Solution
Knowledge Check

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθA thin uniform heavy rod of length l hangs from a horizontal axis passing through one end. The initial angular velocity ω that must be imparted to it to rotate it through 90∘ is :
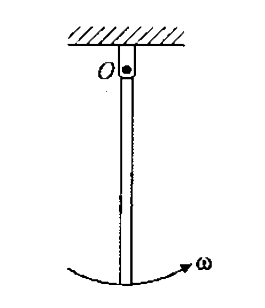 A√g/lB√3g/lC√(2g/l)D√6g/l
A√g/lB√3g/lC√(2g/l)D√6g/lA thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
Adirectly proportional to its length and inversely proportional to its massBindependent of mass and inversely proportional to the square root of its lengthCdependent only upon the acceleration due to gravity and the length of the barDdirectly proportional to its length and inversely proportional to the acceleration due to gravity

A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

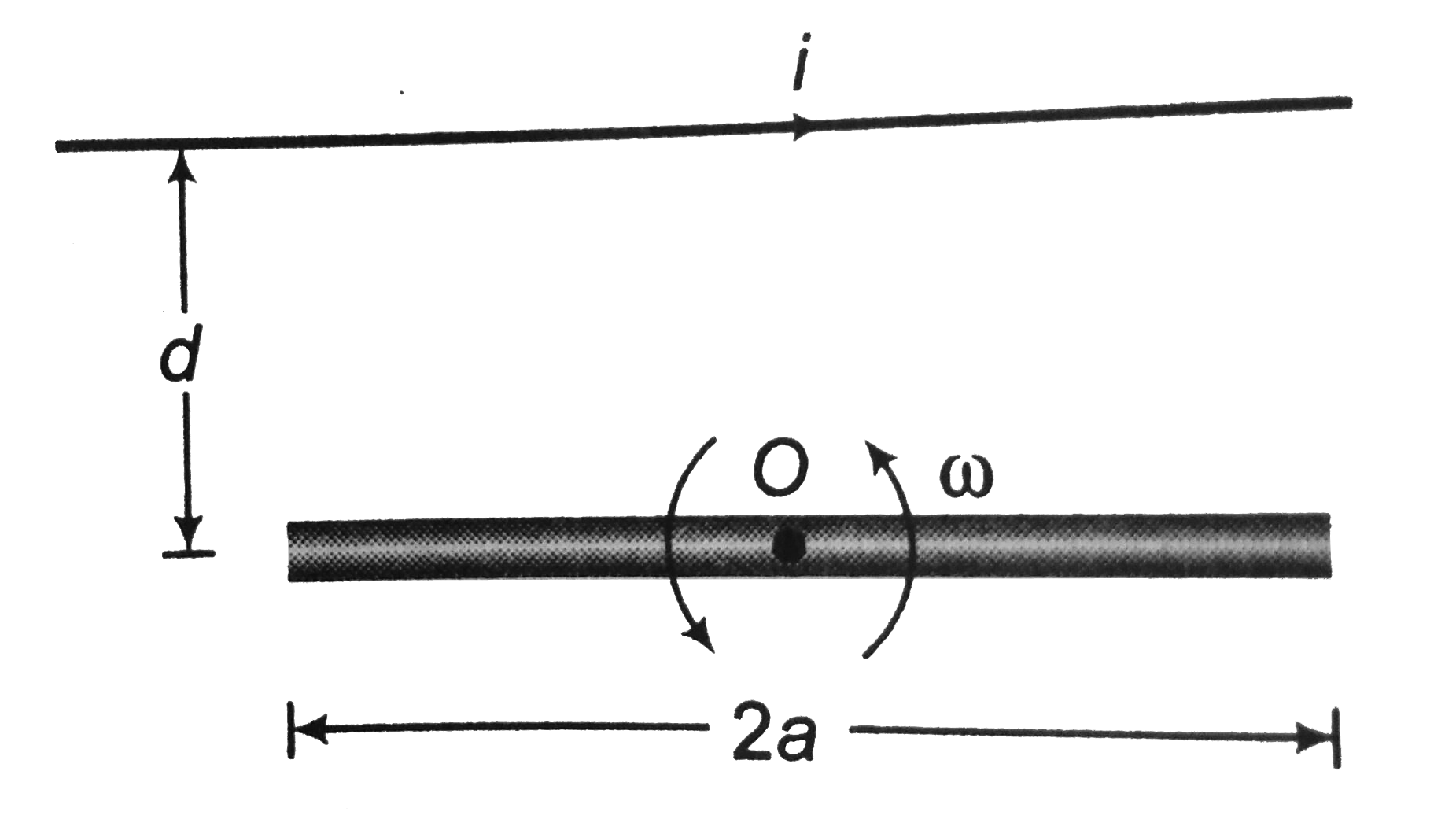
View SolutionA rod of length 2a is free to rotate in a vertical plane, about a horizontal axis O passing through its mid-point. A long straight, horizontal wire is in the same plane and is carrying a constant current i as shown in figure. At initial moment of time, the rod is horizontal and starts to rotate with constant angular velocity ω, calculate emf induced in the rod as a function of time.
View SolutionA thin rod of mass m and length 2L is made to rotate about an axis passing through its center and perpendicular to it. If its angular velocity changes from O to ω in time t, the torque acting on it is
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution
