A smooth fixed rod is inclined at an angle θ to the horizontal. At the bottom end of the rod there is a fixed charge +Q. There is a bead of mas m having charge q that can slide freely on the rod. The equilibrium separation of the bead from fixed charge Q is x0 Find the frequency of oscillation of the bead if it is displaced a little from its equilibrium position.
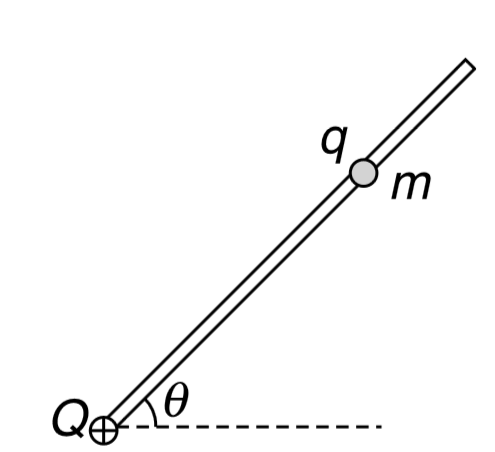
The correct Answer is:f=12π√2gsinθx0
Step by step video, text & image solution for A smooth fixed rod is inclined at an angle theta to the horizontal. At the bottom end of the rod there is a fixed charge +Q. There is a bead of mas m having charge q that can slide freely on the rod. The equilibrium separation of the bead from fixed charge Q is x_(0) Find the frequency of oscillation of the bead if it is displaced a little from its equilibrium position. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
- ELECTROMAGNETIC INDUCTIONBook:ARIHANTChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 3
Explore 12 Videos
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
Similar Questions
A particle of mass m and charge +q is located midway between two fixed charged particles each having a charge +q and at a distance 2L apart. Assuming that the middle charge moves along the line joining the fixed charges, calculate the frequency of oscillation when it is displaced slightly.
View SolutionTwo positive point charges , each Q , are fixed at separation d. A third charge q is placed in the middle. Describe the equilibrium of the third charge.
View Solution
Knowledge Check
A simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
AT=2π ⎷lg+kq2ml2BT=2πCT=2π√lgDwill be greater then 2π√lgA smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
Aqπ√mπε0L3Bq4π(mπε0L3)C2qπ√mπε0L3Dq2π√mπε0L3
A charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View SolutionA massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance L4 from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Δθ from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m.
View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?
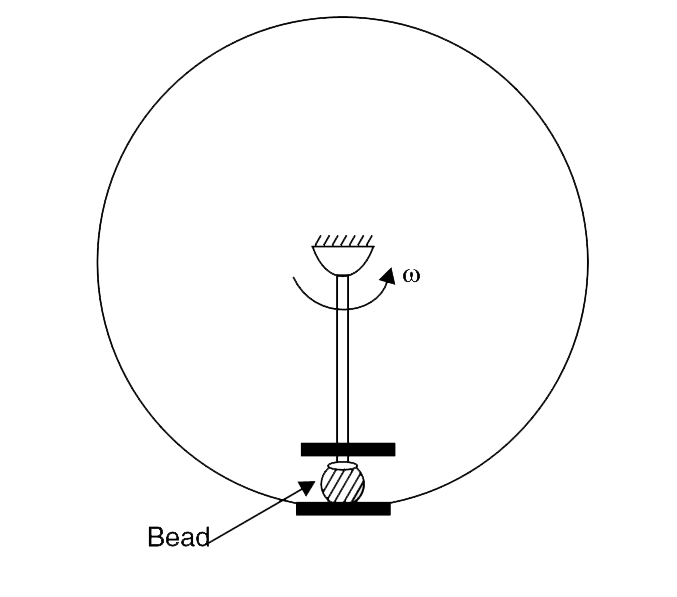
View SolutionTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
View Solution

