An ellipsoidal cavity is carved within a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure. Then
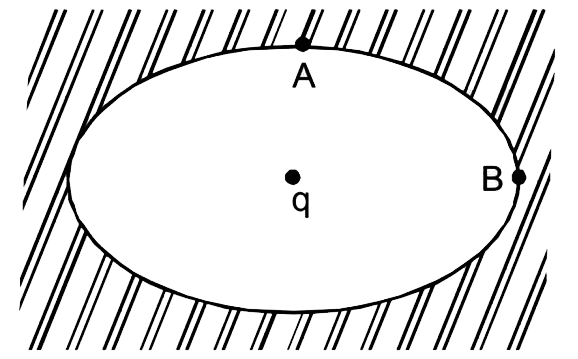
electric field near a in the cavity = electric field near B in the cavity
charge density at A = charge density at B
potential at a = potential at B
total electric field flux through the surface of the cavity is q/ε0
The correct Answer is:C
Under electrostatic condition, all points lying on the conductor are in same potential. Therefore, potential at A=potential at B. Hence, option (C) is correct. From Gauss theorem, total flux through the surface of the cavity will be qε0
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - REASONING TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - MATCH THE COLUME TYPE
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
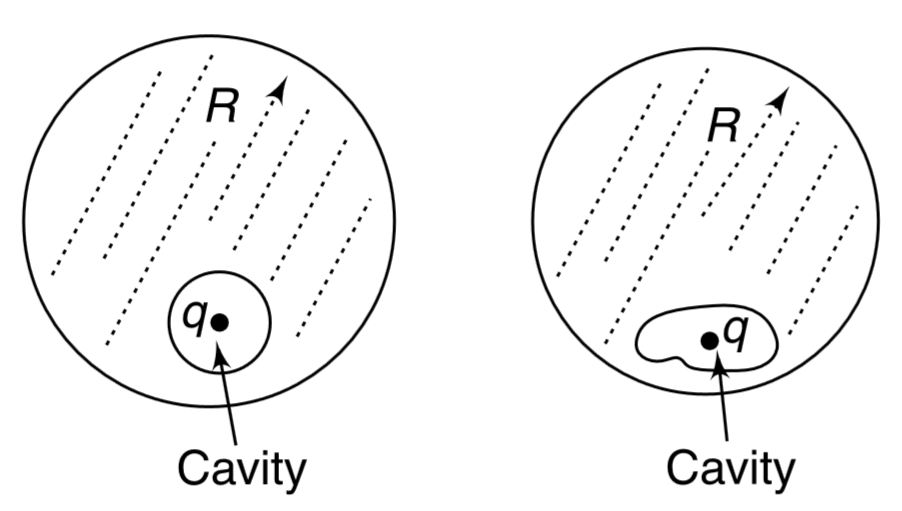
A solid spherical conductor of radius R has a spherical cavity inside it (see figure). A point charge q is placed at the centre of the cavity. (a) What is the potential of the conductor? (b) If the charge q is shifted inside the cavity by a distance Δx, how does the potential of the conductor change? (c) How does your answer to the question (a) and (b) change if the cavity is not spherical and the charge q is placed at any point inside it (see figure) (d) Draw electric field lines in entire space in each case. In which case all field lines are straight lines
View SolutionA charge Q0 is placed at the center of spherical cavity of a conductor and another charge Q is placed outside the conductor as shown in the figure. The correct statement is :
View Solution
Knowledge Check
In front of an earthed conductor a point charge +q is placed a shown in figure
AOn the surface of conductor the net charge is always negativeBOn the surface of conductor at some points charges are negative and at some points charges may be positive distributed non uniformlyCInside the conductor electric field due to point charge is non zeroDNone of theseA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in figure. All the three charges are positive
The force on the charge at the centre isAtowards leftBtowards rightCupwardDzeroThere is a cubical cavity inside a conducting sphere of radius R. A positive point charge Q is placed at the centre of the cube and another positive charge q is placed at a distance 1(>R) from the centre of the sphere. The sphere is earthed
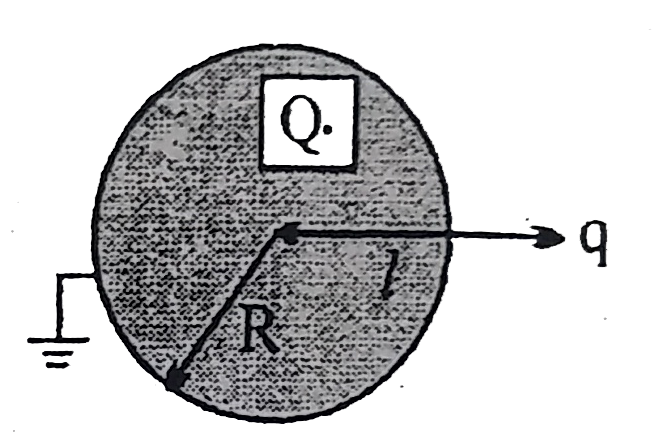
Net charge on the outer surface of conducting sphere isA+QBQ−qR/1C−qR/IDnone
A point charge q is placed with in the cavity of an electrically neutral conducting shell whose outer surface has spherical shape. Then,
View SolutionA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
View SolutionThere is a conductor with cavity of radius R as shown in figure. A point charge Q is placed at R/2 distance from centre of cavity.
A point P is at r distance from centre of conductor. Then,
View SolutionConsider a conductor with a spherical cavity in it. A point charge q0 is placed at the centre of cavity and a point charge Q is placed outside conductor.
Statement-1: Total charge induced on cavity wall is equal and opposite to the charge inside
Statement-2: If cavity is surrounded by a Gaussian surface, where all parts of Gaussian surface are located inside the conductor, ∮→Ed→A=0 hence q∈duceed=−q0
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
View Solution