A circular ring of radius R with uniform positive charge density $λ$ per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P $(R \sqrt{3}, 0, 0)$ on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\sqrt{\frac{λ q}{2 \in_{0} m}}$

K.E. at 'P' must be sufficient to reach the charge particle at the centre of the ring.
${(M E)}_{P} = {(M E)}_{centre of ring}$
$\frac{1}{2} m v^{2} + \frac{K π λ \times 2 π R q}{\sqrt{{(R^{2} + \sqrt{3} R)}^{2}}} = O + \frac{K \times λ 2 π R q}{R}$
$v = \sqrt{\frac{λ q}{2 \in_{0} m}} (∵ K = \frac{1}{4 π \in_{0}})$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circular ring of radius R and uniform linear charge density $+ λ C / m$ are kept in x - y plane with its centre at the origin. The electric field at a point $(0, 0, \frac{R}{\sqrt{2}})$ is
A $\frac{λ}{3 \sqrt{3} ε_{0} R}$
B $\frac{2 λ}{3 \sqrt{3} ε_{0} R^{2}}$
C $\frac{2}{3 \sqrt{3}} \frac{λ}{ε_{0} R}$
Dnone the these
Question 2 - Select One or More
A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point $(0, 0, z_{0})$ where $z_{0} > 0$ . Then the motion of P is
A(a) periodic, for all values of $z_{0}$ satisfying $0 < z_{0} < \infty$
B(b) simple harmonic, for all values of $z_{0}$ satisfying $0 < z_{0} \leq R$
C(c) approximately simple harmonic, provided $z_{0} < < R$
D(d) such that P crosses O and continues to move along the negative z axis towards $z = - \infty$
Question 3 - Select One
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field $\to E$ at the centre O is

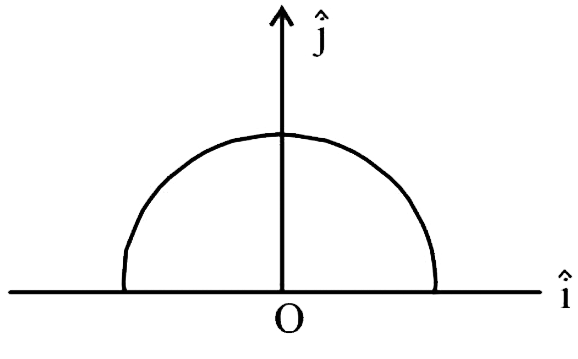A(a) $\frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
B(b) $- \frac{q}{4 π^{2} ε_{0} r^{2}} ˆ j$
C(c) $- \frac{q}{2 π^{2} ε_{0} r^{20} ˆ j}$
D(d) $\frac{q}{2 π^{2} ε_{0} r^{2}} ˆ j$

ALLEN-MISCELLANEOUS-Exersice-04[B]

Home
Ask Doubt
Profile