A particle of mass m and charge −q moves along a diameter of a uniformly charged sphere of radius R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed R .
The correct Answer is:12π√qQ4π∈0mR3
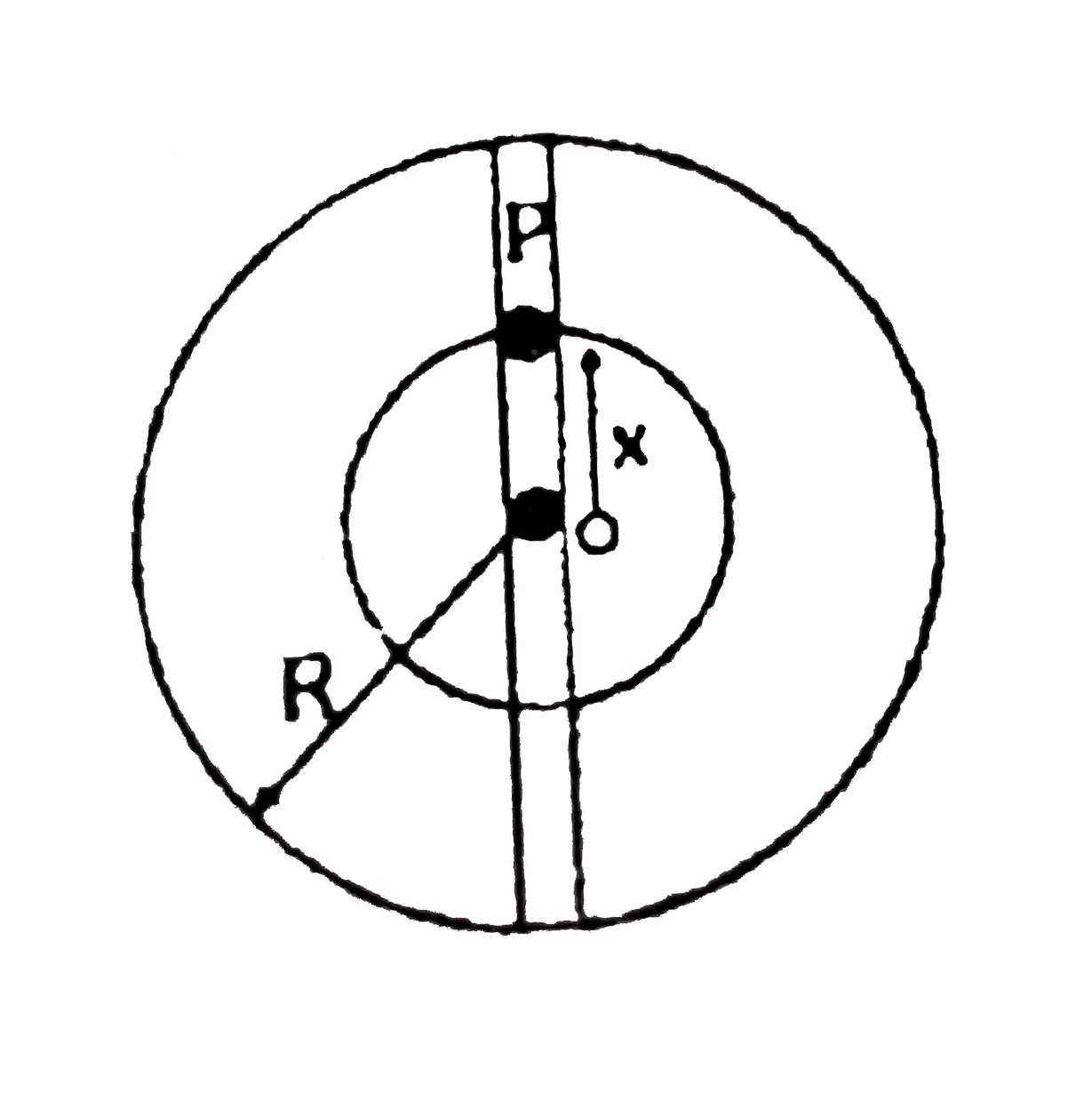
Force on charge at position P
=−(14π∈0×QR3x)q=−mω2x
T=2π√qQ4π∈0×mR3
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-04[B]
Explore 16 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-05(A)
Explore 35 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 9
Explore 2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
A particle of mass m and charge -q moves along a diameter of a uniformluy charged sphere of radinus R and carrying a total charge +Q. Find the frequency of S.H.M. of the particle if the amplitude does not exceed .
View SolutionCalculate the self potential energy of charge q distributed over the surface of a hollow sphere of radius R. What happens to this self energy when R=0, or when the charge is an ideal point charge?
View Solution
Knowledge Check
A particle of mass m and charge -q moves diametrically through a uniformily charged sphere of radius R with total charge Q. The angular frequency of the particle's simple harminic motion, if its amplitude lt R, is given by
A√14πε0qQmRB√14πε0qQmR2C√14πε0qQmR3D√14πε0mqQA bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)
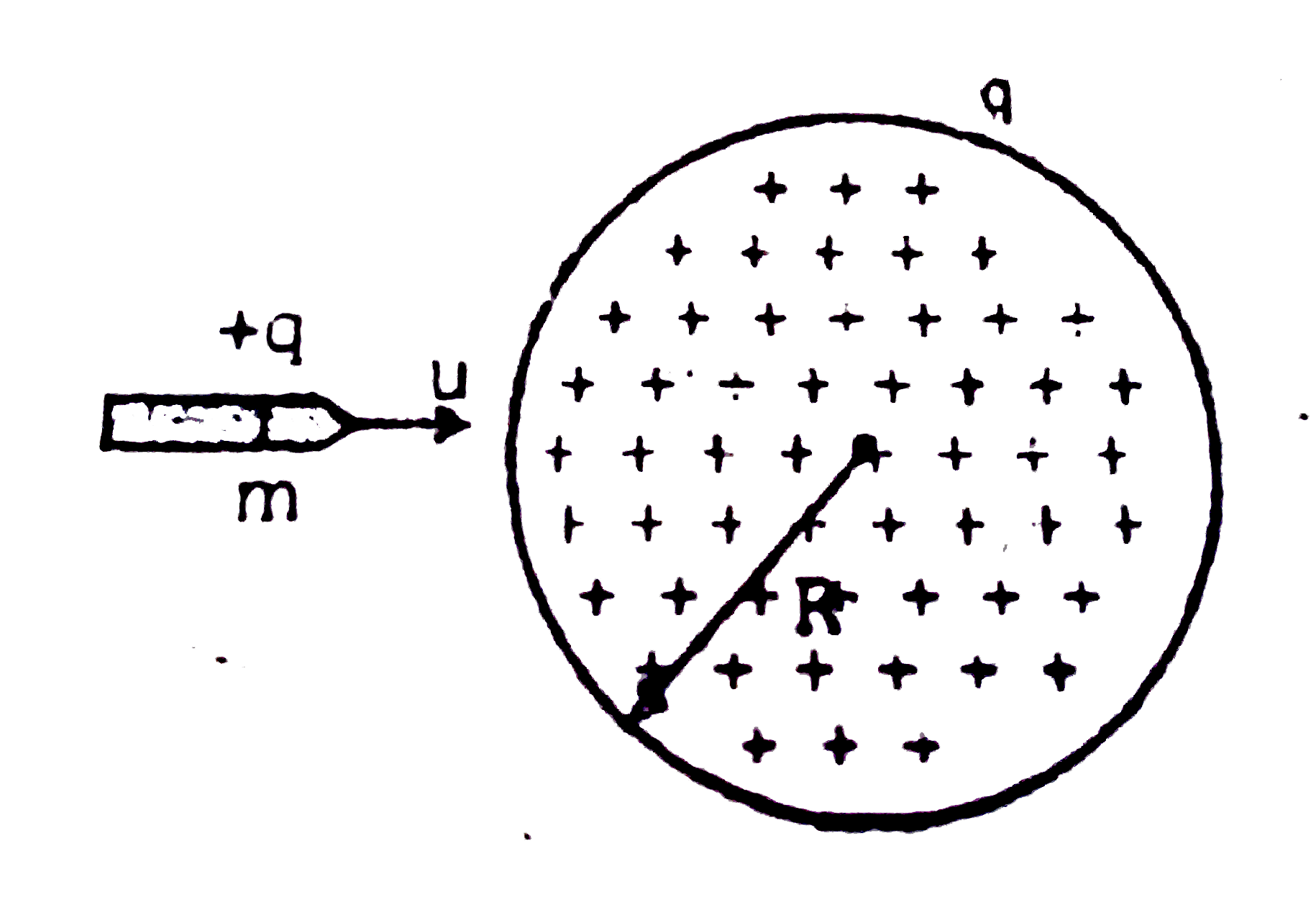 Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mR
Aq√2πε0mRBq√4πε0mRCq√8πε0mRD√3q√4πε0mRA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of B
A uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionA charge particle of charge q & mass m is projected towards the center of uniformly charged ring of radius R& carrying a charge Qfrom a distance of √3R from the center along the axis,find the minimum value of velocity of projection (in ms ) so that particle reaches to x=−∞ where x - axis is along the axis of ring & center of ring is at origin.(given Q=6μc,q=3μc,m= 2gm,R=1m )
View SolutionA conducting sphere of radius 2R carrying charge Q is joined to an uncharged conducting sphere of radius R. Find the charge flow through cinnecting wire.
View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionCalculate amount of charge flow, when a conducting sphere of radius R and carrying a charge Q, is joined to an uncharged conducting sphere of radius 2R.
View Solution

