An isolated conducting sphere of charge Q and radius R is connected to a similar uncharged sphere (kept at a large distance) by using a high resistance wire. After a long time is the amount of heat loss?
To solve the problem of heat loss when an isolated conducting sphere of charge Q and radius R is connected to an uncharged sphere, we can follow these steps:
Step 1: Understand the Initial Conditions
Initially, we have one conducting sphere with charge Q and radius R. The second sphere is uncharged and is kept at a large distance.
Hint: Remember that the potential energy of a charged sphere depends on its charge and radius.
Step 2: Calculate the Initial Potential Energy
The potential energy Ui of the charged sphere can be calculated using the formula for the potential energy of a charged sphere:
Ui=kQ2R
where k is Coulomb's constant.
Hint: The potential energy is derived from the interaction of the charge with itself.
Step 3: Connect the Spheres
When the two spheres are connected by a high resistance wire, charge will redistribute between them. Since both spheres are identical, after a long time, each sphere will have half of the total charge:
Q1=Q2=Q2
Hint: The total charge remains conserved during the redistribution.
Step 4: Calculate the Final Potential Energy
After the charge redistribution, the potential energy Uf of the system can be calculated as:
Uf=k(Q/2)2R+k(Q/2)2R=2⋅k(Q/2)2R=kQ22R
Hint: Consider that both spheres contribute to the total potential energy after they are connected.
Step 5: Calculate the Heat Loss
The heat loss ΔH can be calculated as the difference between the initial and final potential energy:
ΔH=Ui−Uf=kQ2R−kQ22R
ΔH=kQ2R−kQ22R=kQ22R
Hint: The heat loss is equal to the decrease in potential energy of the system.
Final Answer
The amount of heat loss when the two spheres are connected is:
ΔH=kQ22R
Initially, we have one conducting sphere with charge Q and radius R. The second sphere is uncharged and is kept at a large distance.
The potential energy Ui of the charged sphere can be calculated using the formula for the potential energy of a charged sphere:
Ui=kQ2R
where k is Coulomb's constant.
When the two spheres are connected by a high resistance wire, charge will redistribute between them. Since both spheres are identical, after a long time, each sphere will have half of the total charge:
Q1=Q2=Q2
After the charge redistribution, the potential energy Uf of the system can be calculated as:
Uf=k(Q/2)2R+k(Q/2)2R=2⋅k(Q/2)2R=kQ22R
The heat loss ΔH can be calculated as the difference between the initial and final potential energy:
ΔH=Ui−Uf=kQ2R−kQ22R
ΔH=kQ2R−kQ22R=kQ22R
The amount of heat loss when the two spheres are connected is:
ΔH=kQ22R
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-01
Explore 87 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:SUBJECTIVE QUESTION
Explore 9 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
An isolated conducting sphere of charge Q and radius R is grounded by using a high resistance wire. What is the amount of heat loss ?
View SolutionA conducting sphere of radius 2R carrying charge Q is joined to an uncharged conducting sphere of radius R. Find the charge flow through cinnecting wire.
View Solution
Knowledge Check
An isolated conduction sphere sphere whose radius R=1 m has a charge q=19nC. The energy density at the surface of the sphere is
Aε02J/m3Bε0J/m3C2ε0J/m3Dε0/3Jm3A hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.
Apotential at A and B is same.Bpotential at O and B is same.Cpotential at O and C is same.Dpotential at A,B,C and O is same.A metallic sphere of radius R having charge Q is connected to an uncharged sphere of radius 3R. The amount of charge flown through connecting wire is
AQ/4BQ/2C3Q/4DQ
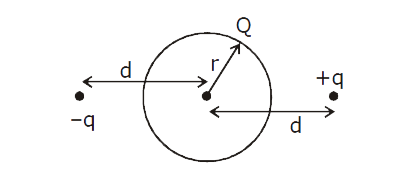
A solid conducting sphere of radius r is having a charge Q and point charges +q and -q are kept at distance d from the centre of sphere as shown in the figure. The electric potential at the centre of solid sphere
(assume potential to be 0 at infinity)
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View Solution

