A hollow spherical conductor of radius R has a charge Q on it. A small dent on the surface decreases the volume of the spherical conductor by 2%. Assume that the charge density on the surface does not change due to the dent and the electric field in the dent region remains same as other points on the surface.
(a) ΔE is the electrostatic energy stored in the electric field in the shallow dent region and E is the total electrostatic energy of the spherical shell. Find the ratio ΔEE
(b) Using the ratio obtained in part (a) calculate the percentage change in capacitance of the sphere due to the dent.
The correct Answer is:(a) 1150
(b) 0.67 %
Step by step video, text & image solution for A hollow spherical conductor of radius R has a charge Q on it. A small dent on the surface decreases the volume of the spherical conductor by 2%. Assume that the charge density on the surface does not change due to the dent and the electric field in the dent region remains same as other points on the surface. (a) Delta E is the electrostatic energy stored in the electric field in the shallow dent region and E is the total electrostatic energy of the spherical shell. Find the ratio (Delta E)/(E) (b) Using the ratio obtained in part (a) calculate the percentage change in capacitance of the sphere due to the dent. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A resistance R and a capacitor having capaci- tance C are connected to an alternating source having emf v=V0sin(ωt).It is given that ω=1√3RC
(a) Plot the variation of power supplied by the source as a function of time. Mark the maximum and minimum values of power in the graph.
(b) How does the plot change if capacitor is removed and only R remains connected to the source?
(c) Plot the graph when only C remains connected to source and R is removed.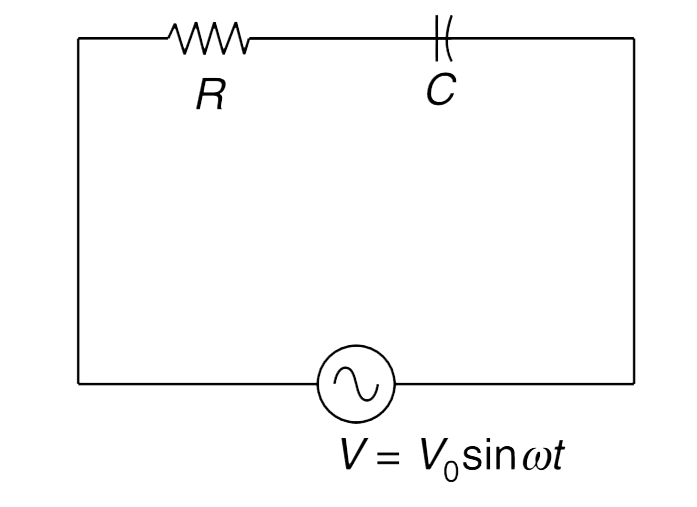
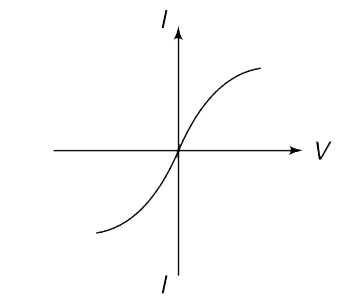
View SolutionThe current-voltage graph for a resistor is as shown in the figure. Is it right to say that resistance decreases as the current through it increases ?
View SolutionA spherical charged conductor has surface density of charge as σ. The electric field intensity on its surface is E. If the radius of the surface is doubled, keeping σ uncharged, what will be the electric field intensity on the new sphere ?
View SolutionA charged spherical conductor has a surface density of 0.07 C cm^(-2) . When the charge is increased by 4.4 C , the surface density changes to 0.084 C cm^(-2). Find the initial charge and capacitance of the spherical conductor.
View SolutionA spherical charged conductor has σ as the surface density of charge. The electric field on its surface is E. If the radius of the sphere is doubled keeping the surface density of charge unchanged, what will be the electric field on the surface of the new sphere -
View Solutionकिसी खोखले गोलाकार आवेशित चालक के अन्दर तथा चालक के सतह पर विभव का मान कितना होता है ?
View Solutionr त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर q आवेश एकसमान रूप से वितरित है।
गोल के अंदर विद्युत क्षेत्र क्या होगा
View SolutionA hollow spherical conductor of radius 2 cm is electrifled with 20 statC. Determine the surface density of charge on the external surface of the conductor.
View SolutionA hollow spherical conductor of radius 3 cm is charged with a charge of 36 pi C. The surface density of charge on the inner surface of the hollow conductor is
View SolutionA hollow spherical conductor of radius 3 cm is charged with a charge of 36πC.
The surface density of charge on the outer surface of the hollow conductor is
View SolutionA number of spherical conductors of different radii are charged to same potential. The surface charge density of each conductor is related with its radius as
View SolutionELECTROSTATICS OF CONDUCTORS | ELECTRIC FIELD AT SURFACE OF CHARGED CONDUCTOR
View Solutionएक गोलाकार आवेशित चालक का आवेश घनत्व σ है। इसके पृष्ठ पर वैद्युत क्षेत्र E है। यदि गोले की त्रिज्या उसका आवेश घनत्व अपरिवर्तित रखते हुए दोगुनी कर दी जाए, तो नए गोले के पृष्ठ पर वैद्युत क्षेत्र होगा
View SolutionAn uncharged conductor of arbitrary (non-spherical)shape, has a spherical cavity with a point charge q kept at its centre. The induced surface charge densities at outer surface of conductor and inner surface of cavity in electrostatic condition are respectively
View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V, now radius is halved keeping surface charge density to be constant. Then the new values will be
View Solution