A large non rotating star of mass M and radius R begins to collapse under its own gravity and ultimately becomes very small (nearly a point mass). Assume that the density remains uniform inside the sphere in any stage. Plot the variation of gravitational field intensity (well, you can call it cceleration due to gravity) at a distance R2from the centre vs the radius (r) of the star.
The correct Answer is:(##IJAPHYV01C07E01031_A01##)
Step by step video, text & image solution for A large non rotating star of mass M and radius R begins to collapse under its own gravity and ultimately becomes very small (nearly a point mass). Assume that the density remains uniform inside the sphere in any stage. Plot the variation of gravitational field intensity (well, you can call it cceleration due to gravity) at a distance (R)/(2)from the centre vs the radius (r) of the star. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionThere is a uniform sphere of mass M and radius R. Find the strength G and the potential varϕ of the gravitational field of this sphere as a function of the distance r from its centre (with r<R and r>R). Draw the approximate plots of the functions G(r) and φ(r).
View Solution
Knowledge Check
An extremely small and dense neutron star of mass M and radius R is rotating with angular velocity ω. If an object is placed at its equator, then it will remain stuck to it due to gravity, if
AM>RωGBM>R2ω2GCM>R3ω3GDM>R2ω2GA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2A small section of area ΔA is removed from a uniform spherical shell with surface mass density σ and radius R as shown in the figure . Find the magnitude of gravitational field intensity at point P due to the remaining mass .
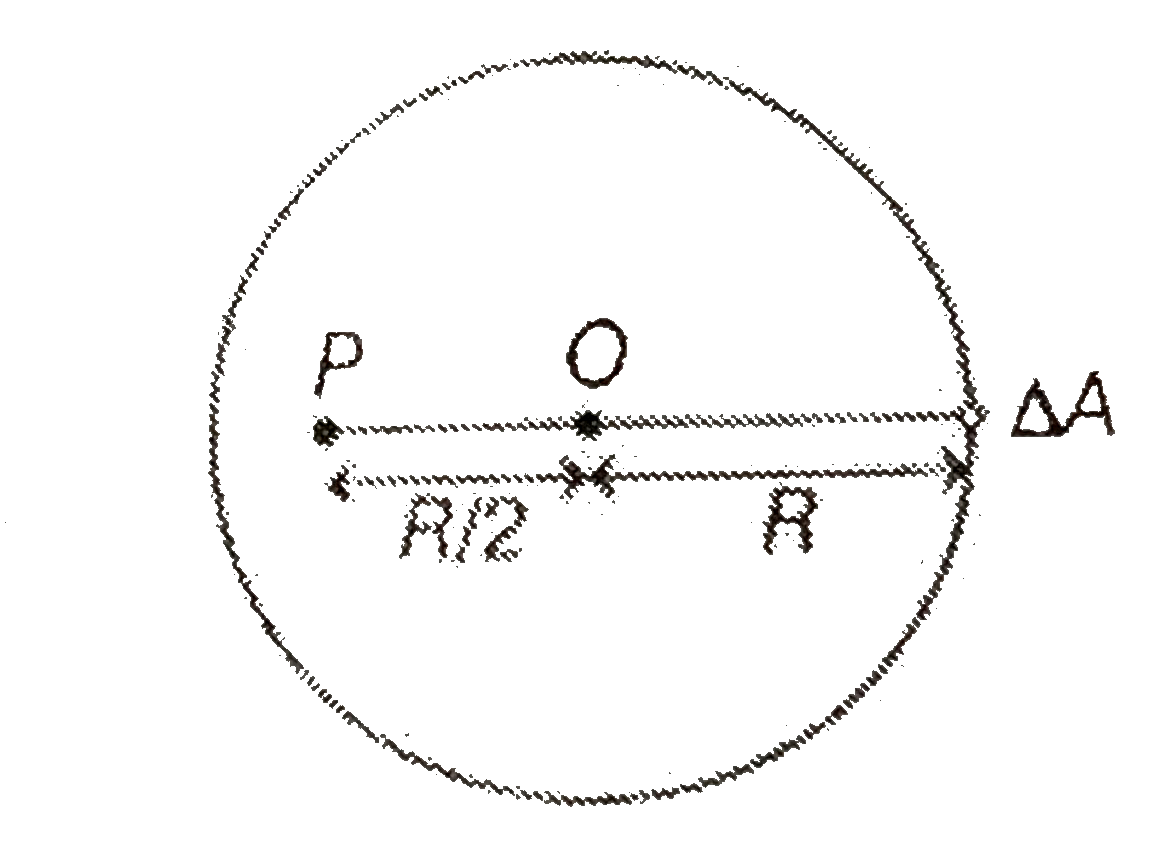 A4σΔAG9R2B4σΔAGR2CσΔAGR2Dzero
A4σΔAG9R2B4σΔAGR2CσΔAGR2Dzero
A solid shere of mass m and radius r is placed inside a hollow spherical shell of mass 4m and radius 4r find gravitational field intensity at
(a) r<y<2r (b) 2r<y<8r (c) y>8r
here coordinate is measured from the point of contact of the sphere and the shell
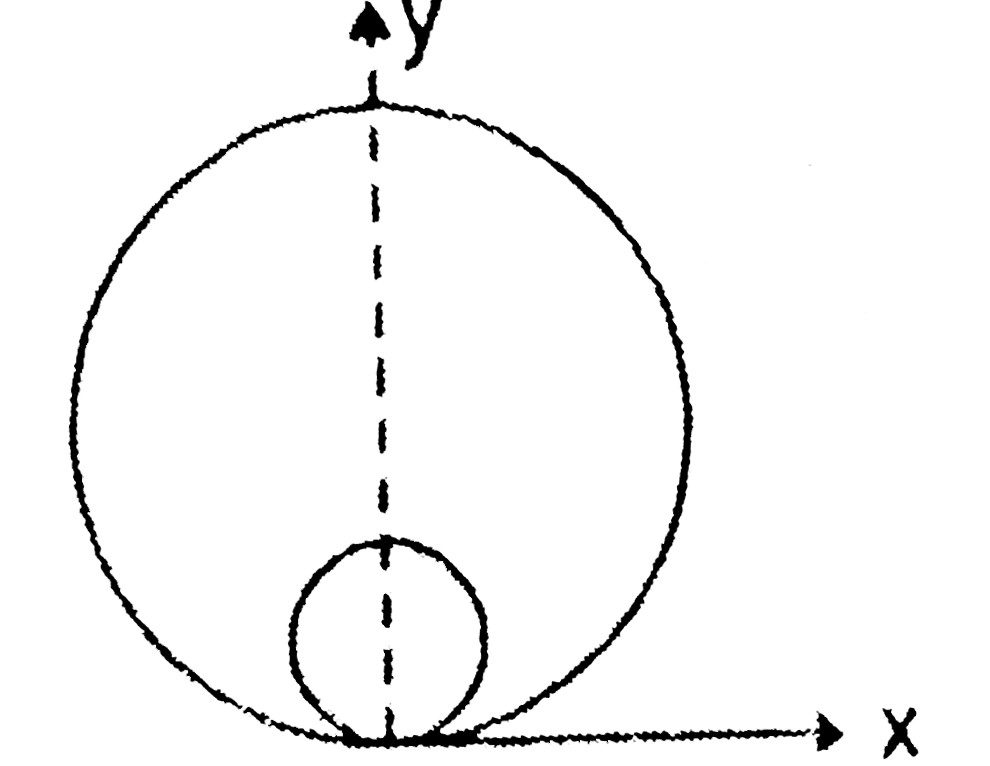 .
.
View SolutionA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
View SolutionA uniform solid sphere of radius R produces a gravitational acceleration ag on its surface. At what two distances from the centre of the sphere the acceleration due to gravity is ag/4 ?
View SolutionThere is one long non-conducting solid cylinder of radius R. The volume charge density is given by ρ=kx2 where k is a constant and x is the distance of the point from centre of cylinder. Electric field intensity inside the cylinder at a distance x from the centre is
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View Solution
