(i) A spinning disk has a hole at its centre. The surface of the disk is horizontal and a small block A of mass m = 1 kg is placed on it.
![(i) A spinning disk has a hole at its centre. The surface of the disk is horizontal and a small block A of mass m = 1 kg is placed on it. Block A is tied to a light inextensible string, other end of which passes through the hole and supports another block B of mass M = 2 kg. The coefficient of friction between A and the disk surface is 0.5. It was observed that the disk is spinning with block A remaining at rest relative to the disk. Block B was found to be stationary. It was estimated that length of horizontal segment of the string (r) was anywhere between 1.0 m to 1.5 m. With this data what estimate can be made about the angular speed (omega) of the disk. [g = 10 m//s^(2)] (ii) A spring has force constant equal to k = 100 Nm^(–1). Ends of the spring are joined to give it a circular shape of radius R = 20 cm. Now the spring is rotated about its symmetry axis (perpendicular to its plane) such that the circumference of the circle increases by 1%. Find the angular speed (omega). Mass of one meter length of the spring is lambda = 0.126 gm^(–1).](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C03_E01_037_Q01.png)
Block A is tied to a light inextensible string, other end of which passes through the hole and supports another block B of mass M = 2 kg. The coefficient of friction between A and the disk surface is 0.5. It was observed that the disk is spinning with block A remaining at rest relative to the disk. Block B was found to be stationary. It was estimated that length of horizontal segment of the string (r) was anywhere between 1.0 m to 1.5 m. With this data what estimate can be made about the angular speed (ω) of the disk. [g=10m/s2] (ii) A spring has force constant equal to k=100Nm–1. Ends of the spring are joined to give it a circular shape of radius R = 20 cm. Now the spring is rotated about its symmetry axis (perpendicular to its plane) such that the circumference of the circle increases by 1%. Find the angular speed (ω). Mass of one meter length of the spring is λ=0.126gm–1.
The correct Answer is:(i) √15<ω√16.67rad/s
(ii) 500rads−1
Step by step video, text & image solution for (i) A spinning disk has a hole at its centre. The surface of the disk is horizontal and a small block A of mass m = 1 kg is placed on it. Block A is tied to a light inextensible string, other end of which passes through the hole and supports another block B of mass M = 2 kg. The coefficient of friction between A and the disk surface is 0.5. It was observed that the disk is spinning with block A remaining at rest relative to the disk. Block B was found to be stationary. It was estimated that length of horizontal segment of the string (r) was anywhere between 1.0 m to 1.5 m. With this data what estimate can be made about the angular speed (omega) of the disk. [g = 10 m//s^(2)] (ii) A spring has force constant equal to k = 100 Nm^(–1). Ends of the spring are joined to give it a circular shape of radius R = 20 cm. Now the spring is rotated about its symmetry axis (perpendicular to its plane) such that the circumference of the circle increases by 1%. Find the angular speed (omega). Mass of one meter length of the spring is lambda = 0.126 gm^(–1). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?

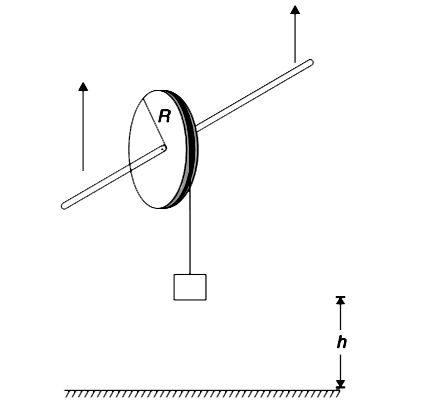
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionA block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:

View SolutionA block of mass M is placed on a horizontal surface. It is tied with an inextensible string that passes through ideal pulleys. A mass m is connected to the pulley as shown. For what value of m, the block M will accelerate towards the fixed pulley ?
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
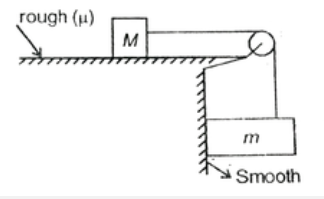
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionA light thread is wound on a disk of mass m and other end of thread is connected to a block of mass m, which is placed on a rough ground as shown in diagram. Find the minimum value of coefficient of friction for which block remain at rest.

View Solutionद्रव्यमान 10 किग्रा का एक ब्लॉक एक क्षैतिज मेज पर रखा है जिससे एक डोरी बँधी है | डोरी का दूसरा सिरा मेज के सिरे पर लगी घर्षण रहित घिरनी के ऊपर से गुजरता है तथा इस सिरे पर द्रव्यमान 20 किग्रा का बाँट बँधा है | यदि मेज व ब्लॉक के बीच घर्षण गुणांक 0.5 है, तो ज्ञात कीजिए : (a) डोरी में तनाव, तथा (b) निकाय का त्वरण | (g=9.8 मी/से2)
View Solution100 किग्रा द्रव्यमान का ब्लॉक A, 200 किग्रा द्रव्यमान के ब्लाक B पर रखा हुआ है तथा चित्र में दिखाए अनुसार एक दीवार से बंधा हुआ है। ब्लॉक A और B के बीच घर्षण गुणांक 0.2 तथा ब्लॉक B और जमीन के बीच घर्षण गुणांक 0.3 है। ब्लॉक B को गति देने के लिये न्यूनतम लगाया गया बल F होगा (g = 10 मी से−2)
View Solutionएक खुरदरे क्षैतिज तल पर M=5kg द्रव्यमान का एक गुटका रखा है। गुटके एवं तल के बीच घर्षण गुणांक 0.2 है और F=40N हो तो गुटके का त्वरण होगा :
View SolutionA circular disk with a tube in diameter is placed horizontally. A block of mass 1 kg is placed as shown. Coefficient of friction between all surfaces of contact with the block and hose mu=2/5 is. Disc 25 "मी/से"^2 Is accelerated by acceleration. Find the acceleration of the block relative to the disk
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View Solution1 किग्रा का एक ब्लॉक एक ट्रक में क्षैतिज तल पर रखा है। ब्लॉक तथा तल के बीच स्थैतिक घर्षण गुणांक 0.6 है। यदि ट्रक का त्वरण 5 मी/सेकण्ड2 हो तो ब्लॉक पर आरोपित घर्षण बल क्या होगा?
View Solution

