Doubtnut Promotions Sticky

Let F and G be two real-valued function defined on R (the set of all real numbers)
F(x)={|x+1|x{:(,xle0,),(,xgt0,):}G(x)={:{(,|x|+1,),(,-|x-2,):}x≤1x>1 and H(x)=F(x)+G(x).
Point of discontinuity of H(x) are

A

x=0

B

x=1

C

x=2

D

x=−1

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A, B

We have, F(x)=⎧⎪⎨⎪⎩−(x+1)(x+1)(x)x<−1−1≤x≤0x>0
and G(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩−x+1x+1x−22−x−∞<x≤00<x≤11<x<2x≥2
H(x)=F(x)+G(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩−(x−1−x+1=−2x)(x+1)−x+1=2x+(x+1)=2x+1x+(x−2)=2x−2x+2−x=2−∞<x≤−1−1≤x≤00≤x≤11<x<2x≥2
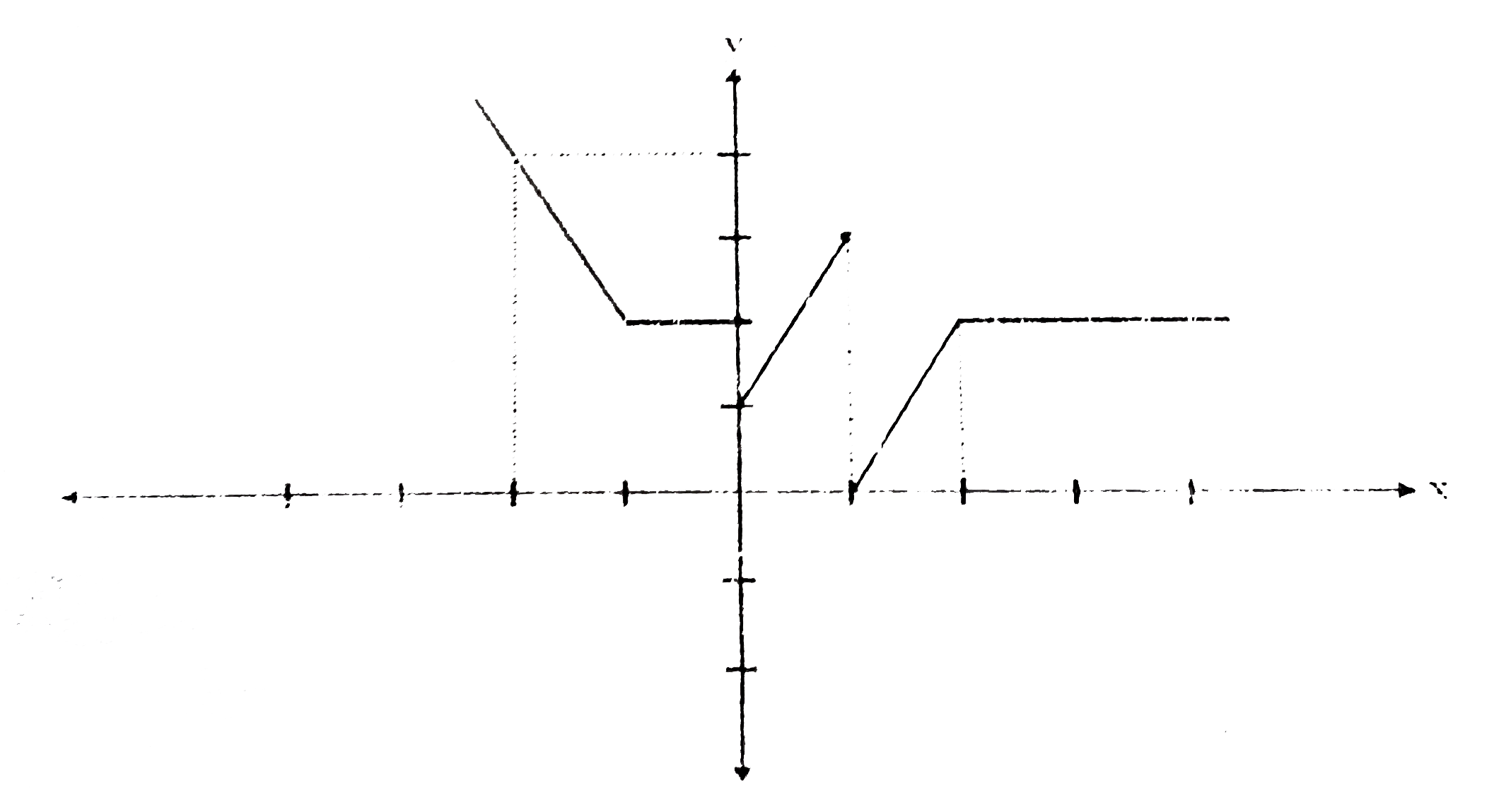ocr_image Graph of H(x)
Clearly from the graph, H(x) is discontinous at
x=0 and x=1, i.e., 2 points of discontinuity
∴A&B
Graphically,
Area under curve from −2→2
=(12×2×1×1)+(2+1)+(12×2×1×1)+(12×2×1)
=(1+2)+2+(1+1)+1
=3+2+2+1=8

|
Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let F and G be two real-valued function defined on R (the set of all real numbers)
    F(x)={|x+1|x{:(,xle0,),(,xgt0,):}G(x)={|x|+1−∣x−2{:(,xle1,),(,xgt1,):}andH(x)=F(x)+G(x).<br>Thevalueofdef∈ite∫egralint_(-2)^(2) H(x) dx is equal to

    A4
    B7
    C8
    D12
  • Question 2 - Select One

    Let f(x)={1+x0≤x≤23−x2<x≤3, then the points of discontinuity of g(x)=f[f(x)] is/are

    Aonly at x=1
    Bx=2,3
    Conly at x=3
    Dx=1,2
  • Question 3 - Select One

    A function is defined as f(x)={ex,x≤0|x−1|,x>0, then f(x) is

    Af(x) is differentiable at x=0
    Bf(x) is continuous at x = 0 ,1
    Cf(x) is differentiable at x=1
    DNone of the above