Let f(x)=x2−3x+2
g(x)=f(|x|)
h(x)=|g(x)|
are three functions. The complete set of values of x, for which the equation h(x)+g(x)=0 is satisfied, is
A
x∈[1,2]
B
x∈[−2,−1]∪[1,2]
C
x∈[−2,−1]
D
None of these
Video Solution
Text Solution
The correct Answer is:B
h(x)+g(x)=0 is satisfied
if x∈[−2,−1]∪[1,2]
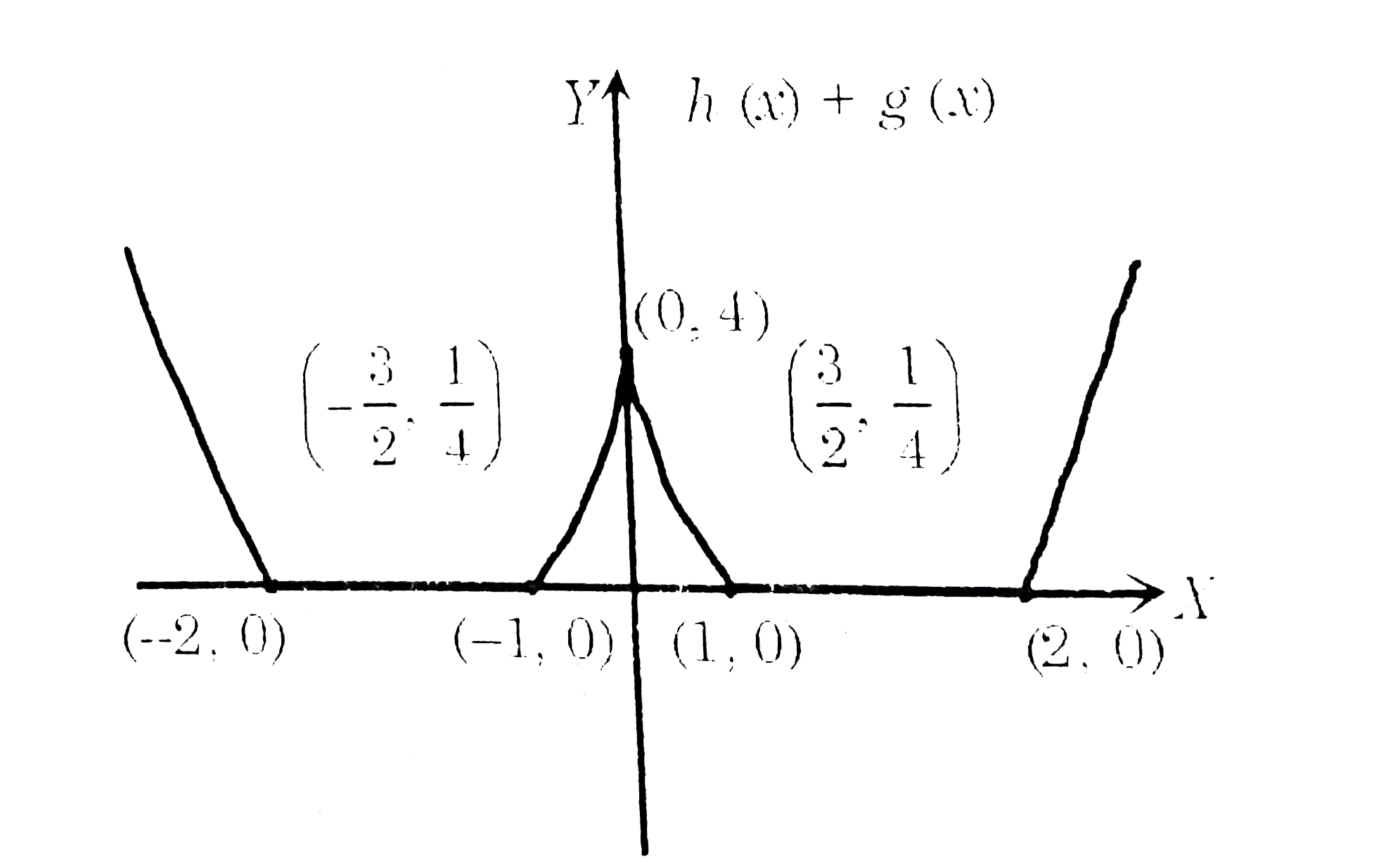
|
Topper's Solved these Questions
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHEMATICS
Explore 51 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:CHEMISTRY
Explore 1 Video
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:part-2 Mathematic
Explore 18 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:CHEMISTRY SECTION-II
Explore 8 Videos
- VECTOR ALGEBRABook:ALLENChapter:VECTOR ALGEBRAExercise:All Questions
Explore 1 Video
Similar Questions
Knowledge Check
Let f(x)=x2−5x+6,g(x)=f(|x|),h(x)=|g(x)|
The set of values of x such that equation g(x)+|g(x)|=0 is satisfied containsA−3B0C2D52Let f(x)=15−|x−10|,x∈R. Then, the set of all values of x, at which the function, g(x)=f(f(x)) is not differentiable, is
A{5,10,15,20}B{5,10,15}C{10}D{10,15}If f(x)=sinlog(√4−x21−x), then the domain of f(x) is ….
AR−{0}BRCR+DR+∪{0}
If f(x)=x, g(x)=√x2 and h(x)=x2x, then the set of values for which the given functions f(x), g(x) and h(x) are identical is :
View SolutionLet f(x)=ex−x and g(x)=x2−x,∀x∈R. Then the set of all x∈R where the function h(x)=(fog)(x) in increasing is :
View SolutionConsider f, g and h be three real valued function defined on R. Let f(x)=sin3x+cosx,g(x)=cos3x+sinx and h(x)=f2(x)+g2(x). Then,
The length of a longest interval in which the function g=h(x) is increasing, is
View SolutionLet f(x)=[x],g(x)=|x|andf{g(x)}=h(x) ,where [.] is the greatest integer function . Then h(-1) is
View SolutionLet f(x)=x,g(x)=1/xandh(x)=f(x)g(x). Then, h(x)=1, if
View Solution