A line divides an equilateral triangle ABC of side 1 unit into two parts with same perimeter and different are S1 and S2 sq. units. If maximum value of S1S2=mn (where m and n coprime), then |m−n| is _____
The correct Answer is:2
x+y=1−x+1−y1
x+y=32
S1S3=12xysin60∘√34=xy√3(√34)=xy=x(32−x)
∵S2=S3−S1
S2S1=1−S1S3=1−xy=1−x(32−x)
S1S3(max)=316 as S2S3=169−1=(79)
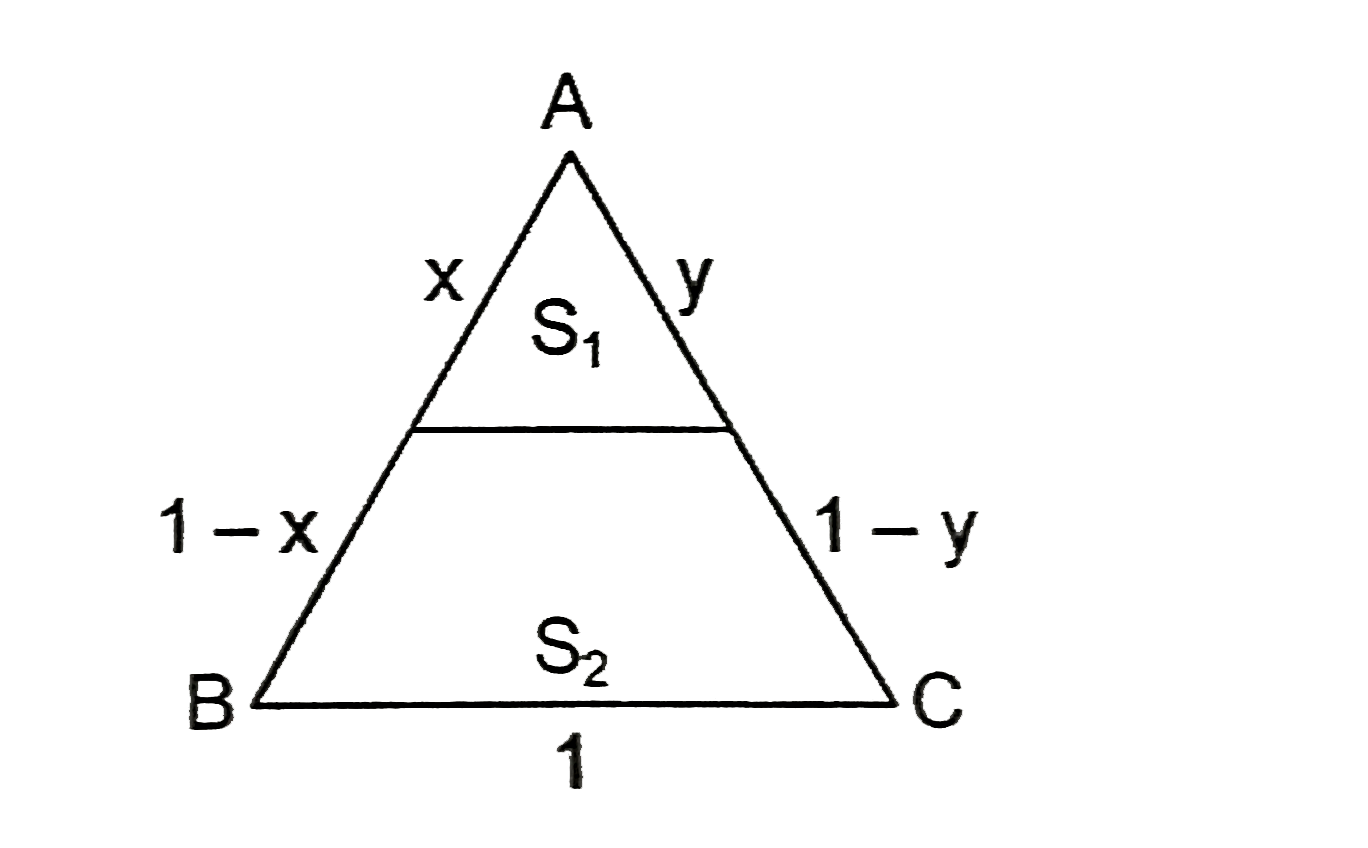
Topper's Solved these Questions
Similar Questions
A line divides an equilateral triangle ABC of side length unity into two parts with same perimeter and areas S1 and S2
The maximum value of S1S2 is
View SolutionA line divides an equilateral triangle ABC of side length unity into two parts with same perimeter and areas S1 and S2
For maximum of minimum ratio S1S2 the line divides the side of the triangle in the ratio
View Solution
Knowledge Check
SN1andSN2 reactions are
ABoth sterespecticBBoth stereoselectiveCStereoselective and Strerepselectfic respectivlyDStereoselective and Strerepselective respectivlyNms−1 is the unit of
APressureBPowerCPotentialDPressure graident
Write any two differences between SN2andSN1 reaction.
View SolutionSubstitution can take place with alkyl halides by two different mechanisms, SN1 and SN2.
View SolutionS2n+1−S2 must be equal to (A) (S1−S2)3(1+122n−1)
View SolutionIf Sn, be the sum of n terms of an A.P; the value of Sn−2Sn−1+Sn−2, is
View SolutionIf 10∑i=1tan−1(39r2+3r−1)=cot−1(mn) (where m and n are coprime) then the value of 2m+n8 is
View SolutionFor a sequence, if Sn=nn+1 then find the value of S10.
View Solution
