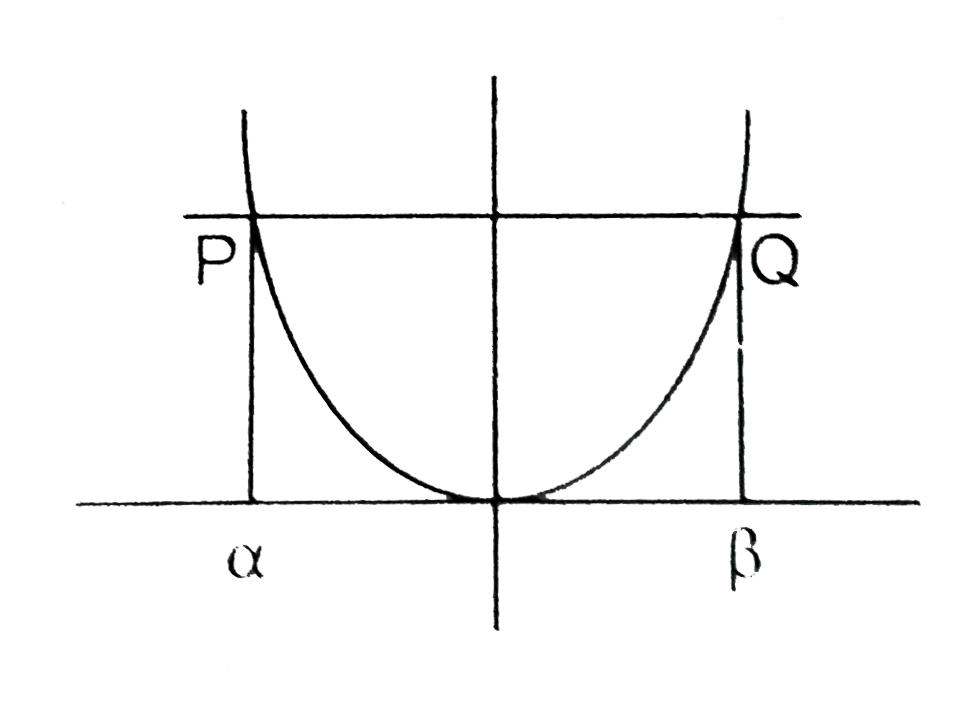
A variable line L intersects the parabola y=x2 at points P and Q whose x- coordinate are α and β respectively with α<β the area of the figure enclosed by the segment PQ and the parabola is always equal to 43. The variable segment PQ has its middle point as M
Which of the following is/are correct?
(β−α) can have more than one real values
(β−α) can be equal to 2
(β−α) can have exactly one real value
α=2+β
The correct Answer is:B
Any two point on y=x2 is P(α,α2),Q(β,β2)
Equation of PQ,y−α2=(α+β)(x−α)
y=(α+β)x−αβ
Required area ∫βα((α+β)x−αβ−x2)dx
⇒β−α=2
Pair of tangents from origin are y=2x and y=−2x
Area ∫10((x2+)−2x)dx=23
Topper's Solved these Questions
Similar Questions
PQ is a diameter of circle x2+y2=4 . If perpendicular distances of P and Q from line x+y=2 are α and β respectively then maximum value of αβ is
View SolutionIf the normal to a parabola y2=4ax at P meets the curve again in Q and if PQ and the normal at Q make angles α and β, respectively with the x -axis, then ∣tanα(tanα+ tanβ )| has the value equal to
View Solution
Knowledge Check
The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16The straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
A4B4√2C8D16The line 4x−7y+10=0 intersects the parabola y2=4x at the points P and Q. The coordinates of the point of intersection of the tangents drawn at the points P and Q are
A(−72,−52)B(52,72)C(−52,−72)D(72,52)
If the normals to the parabola y2=4ax at P meets the curve again at Q and if PQ and the normal at Q make angle α andβ , respectively, with the x-axis, then tanα(tanα+tanβ) has the value equal to 0 (b) −2 (c) −12 (d) −1
View SolutionA line y=mx+1 intersects the circle (x−3)2+(y+2)2=25 at the points P and Q . If the midpoint of the line segment PQ has x-coordinate −35, then which one of the following options is correct ?
View SolutionA variable tangent to the parabola y2=4ax meets the parabola y2=−4ax P and Q. The locus of the mid-point of PQ, is
View SolutionA tangent to the parabola y2=4bx=0 meets the parabola y2=4ax in P and Q. Then the locus of the middle points of PQ is:
View SolutionIf the eccentric angles of two points P and Q on the ellipse x2a2+y2b2 are α,β such that α+β=π2, then the locus of the point of intersection of the normals at P and Q is
View Solution
