The wave function of 3s and $3 p_{z}$ orbitals are given by :
$Ψ_{3 s} = \frac{1}{9 \sqrt{3}} {(\frac{1}{4 π})}^{1 / 2} {(\frac{Z}{σ_{0}})}^{3 / 2} (6 = 6 σ + σ) e^{- σ / 2}$
$Ψ_{3 s_{z}} = \frac{1}{9 \sqrt{6}} {(\frac{3}{4 π})}^{1 / 2} {(\frac{Z}{σ_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2} cos 0,$
$σ = \frac{2 Z r}{n α_{0}}$
where $α_{0} = 1 s t$ Bohr radius , Z= charge number of nucleus, r= distance from nucleus.
From this we can conclude:

A

Number of nodal surface for $3 p_{z}$ & $3 s$ orbitals is equal.

B

The angualr nodal surface of $3 p_{z}$ orbital has the equation $θ = \frac{π}{2}$

C

The radial nodal surfaces of 3 orbital and $3 p_{z}$ orbital are at equal distance from the nucleus.

D

3s electron have greater penetrating power intot he nucleus in comparison to 3p electrons.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

(A) Total nodal surfaces in $3 s = 2$
Total nodal surfaces in $3 p = 2$
(B) Angular node in $3 p, cos θ = 0$
$θ = \frac{π}{2}$
(C) let $\frac{z r}{a_{0}} = x$
Radial nodes in 3s. $(6 - 4 x + \frac{4}{9} x^{2}) = 0$
$\Rightarrow (3 - 2 x + \frac{2}{9} x^{2}) = 0 \Rightarrow 27 - 18 x + 2 x^{2} = 0$
$\Rightarrow x = \frac{18 \pm \sqrt{324 - 216}}{2 \times 2} = \frac{18 \pm \sqrt{108}}{4}$
$x = \frac{9 + 3 \sqrt{3}}{2}, x = \frac{9 - 3 \sqrt{3}}{2}$
Radial nodes in $3 p$ $4 - \frac{2}{3} x = 0 \Rightarrow x = 6$
Hence their radial nodes are not same
(D) it is a fact

Updated on:21/07/2023

|

Class 12 CHEMISTRY TEST PAPERS

Similar Questions

Knowledge Check

For a 3s-orbital
$Φ (3 s) = \frac{1}{a \sqrt{3}} {(\frac{1}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) \in^{- σ / 2}$
where $σ = \frac{2 r Z}{3 a_{σ}}$
What is the maximum radial distance of node from nucleus?
A $\frac{(3 + \sqrt{3}) a_{σ}}{Z}$
B $\frac{a_{σ}}{Z}$
C $\frac{3}{2} \frac{(3 + \sqrt{3}) a_{σ}}{Z}$
D $\frac{3 a_{σ}}{Z}$
For an orbital in $B^{+ 4}$ radial function is :
$R (r) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{\frac{3}{4}} (4 - σ) σ e^{- σ / 2}$
where $σ = \frac{Z r}{a_{0}}$ and $a_{0} = 0.529 Å, Z$ = atomic number, $r =$ radial distance from nucleus.
The radial node of orbital is at distance from nucleous.
A $0.529 Å$
B $2.12 Å$
C $1.06 Å$
D $0.423 Å$
Given the $H -$ atom $R_{n, l} = \frac{1}{9 \sqrt{3}} {(\frac{1}{a_{o}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}$
where $σ = \frac{2 Z r}{n a_{o}}, a_{o} = 0.53 Å$
Select the correct statement for the given orbital ?

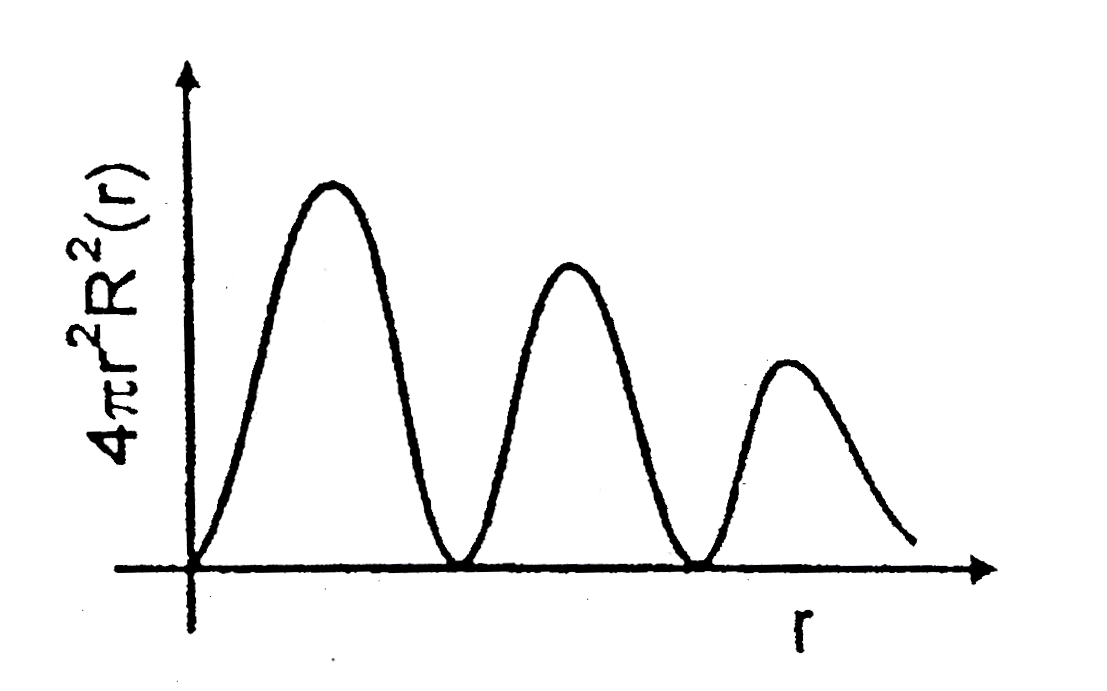AOrbital is $3 s$
BGraph for the given orbital is :
CDistance between radial nodes is equal to $3 \sqrt{3} a_{o}$
DNone of these

Recommended Questions

Home
Ask Doubt
Profile