For an orbital in B+4 radial function is :
R(r)=19√6(za0)34(4−σ)σe−σ/2
where σ=Zra0 and a0=0.529Å,Z = atomic number, r= radial distance from nucleus.
The radial node of orbital is at distance from nucleous.
0.529Å
2.12Å
1.06Å
0.423Å
To find the radial node of the orbital in B+4, we start with the given radial function:
R(r) = \frac{1}{9\sqrt{6}} \left( \frac{Z}{a_0} \right)^{\frac{3}{4}} (4 - \sigma) \sigma e^{-\frac{\sigma}{2}
where σ=Zra0 and a0=0.529Å.
Step 1: Set the radial function to zero
To find the radial nodes, we need to set the radial function R(r) equal to zero:
R(r)=0⟹4−σ=0
Step 2: Solve for σ
From the equation 4−σ=0, we can solve for σ:
σ=4
Step 3: Substitute σ back into its definition
Recall that σ=Zra0. Substituting σ=4 gives:
4=Zra0
Step 4: Solve for r
Rearranging the equation to solve for r:
r=4a0Z
Step 5: Determine the atomic number Z
For B+4, the atomic number Z is 5 (since Boron has an atomic number of 5).
Step 6: Substitute Z and a0 into the equation for r
Now substituting Z=5 and a0=0.529Å:
r=4×0.529Å5
Step 7: Calculate r
Calculating r:
r=2.116Å5=0.4232Å
Final Answer
Thus, the radial node of the orbital is at a distance of approximately:
r≈0.423Å
---
R(r) = \frac{1}{9\sqrt{6}} \left( \frac{Z}{a_0} \right)^{\frac{3}{4}} (4 - \sigma) \sigma e^{-\frac{\sigma}{2}
To find the radial nodes, we need to set the radial function R(r) equal to zero:
From the equation 4−σ=0, we can solve for σ:
Recall that σ=Zra0. Substituting σ=4 gives:
Rearranging the equation to solve for r:
For B+4, the atomic number Z is 5 (since Boron has an atomic number of 5).
Now substituting Z=5 and a0=0.529Å:
Calculating r:
Thus, the radial node of the orbital is at a distance of approximately:
Topper's Solved these Questions
Similar Questions
For a 3s - orbital, value of Φ is given by following realation:
Ψ(3s)=19√3(1a0)3/2(6−6σ+σ2)e−σ/2, where σ=2r.Z3a0
What is the maximum radial distance of node from nucleus?
View SolutionCalcuted the distance of spherical nodes for '3s' orbital from nucleus ?
R3s=19√3a3/20(6−6σ+σ2)eσ2 Where σ=2rna0
View Solution
Knowledge Check
For a 3s-orbital
Φ(3s)=1a√3(1a0)3/2(6−6σ+σ2)∈−σ/2
where σ=2rZ3aσ
What is the maximum radial distance of node from nucleus?A(3+√3)aσZBaσZC32(3+√3)aσZD3aσZGiven the H−atom Rn,l=19√3(1ao)3/2(6−6σ+σ2)e−σ/2
where σ=2Zrnao,ao=0.53Å
Select the correct statement for the given orbital ?
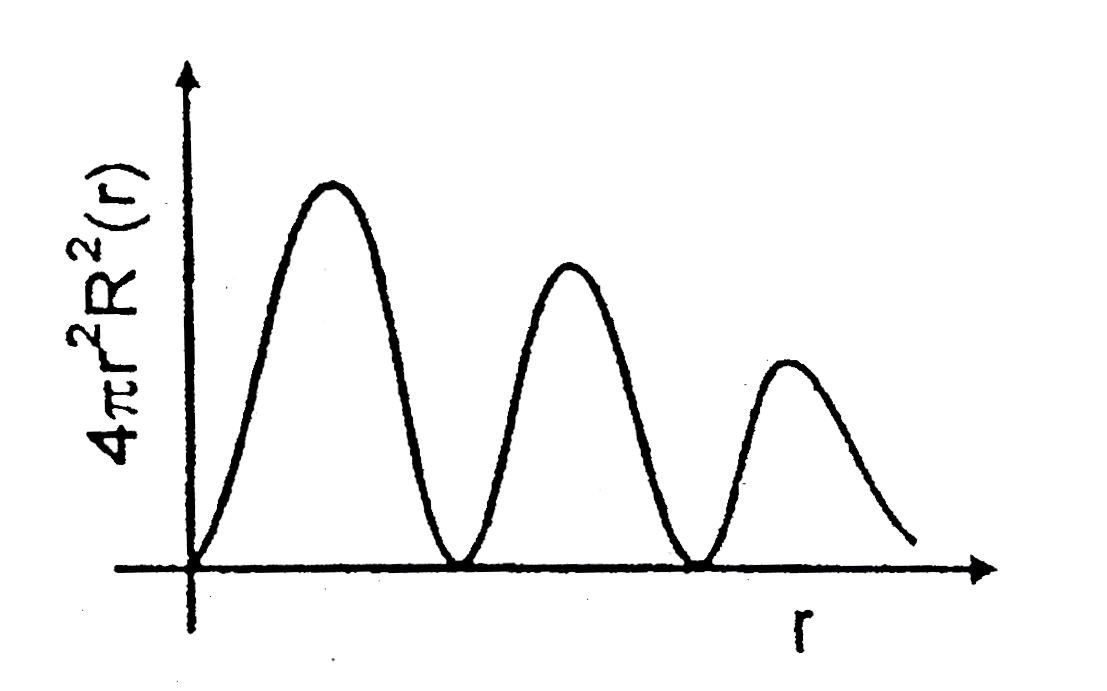 AOrbital is 3sBGraph for the given orbital is :
AOrbital is 3sBGraph for the given orbital is : CDistance between radial nodes is equal to 3√3aoDNone of these
CDistance between radial nodes is equal to 3√3aoDNone of theseAccording to qauntum mechanical model of H-like species, and electron can be represented by a wave function (ψ) which contain all dynamic information about the electron. The nature of wave function depends on the type of the orbital to which the electron belongs. For an orbital
ψ=[√281√3π](1a0)3/2(27−18σ+2σ2)eσ3
Where, σ=(Zra0),r = radial distance from nucleous, a0=52.9pm
The number of radial and angular nodes possible for the orbital given above are respectivelyAzero,zeroB0,2C2,0D2,1
Question : Is the orbital of hydrogen atom 3px ?
STATE 1 : The radial function of the orbital is R(r)=19√6a3/20(4−σ)σe−σ/2,σ=r2
STATE 2 : The orbital has 1 radial node &0 angular node.
View SolutionAccording to qauntum mechanical model of H-like species, and electron can be represented by a wave function (ψ) which contain all dynamic information about the electron. The nature of wave function depends on the type of the orbital to which the electron belongs. For an orbital
ψ=[√281√3π](1a0)3/2(27−18σ+2σ2)eσ3
Where, σ=(Zra0),r = radial distance from nucleous, a0=52.9±
The orbital could possibly be
View SolutionThe Schrodinger wave equation for hydrogen atom of 4s- orbital is given by :
Ψ(r)=116√4(1a0)3/2[(σ2−1)(σ2−8σ+12)]e−σ/2 where a0=1st Bohr radius and σ=2ra0 . The distance from the nucleus where there will be no radial node will be :
View SolutionAccording to qauntum mechanical model of H-like species, and electron can be represented by a wave function (ψ) which contain all dynamic information about the electron. The nature of wave function depends on the type of the orbital to which the electron belongs. For an orbital
ψ=[√281√3π](1a0)3/2(27−18σ+2σ2)eσ3
Where, σ=(Zra0),r = radial distance from nucleous, a0=52.9±
Which of the following represents the position of one of the radial nodes?
View SolutionFor an orbital ,
Ψ300=181√3π(za0)3/2[27−18u+2u2]exp(−u3) where u=zra0
What is the maximum radial distance of node from nucleus of He+ ion ?
View Solution
