If a graph is plotted between T2andr3 for a planet, then its slope will be be (where MS is the mass of the sun)
4π2GM
GM4π2
4πGM
0
Step by step video & image solution for If a graph is plotted between T^(2) and r^(3) for a planet, then its slope will be be (where M_(S) is the mass of the sun) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
If a graph is plotted for the square of period (T2) and mass attached to a spring, its shape will be
A B
B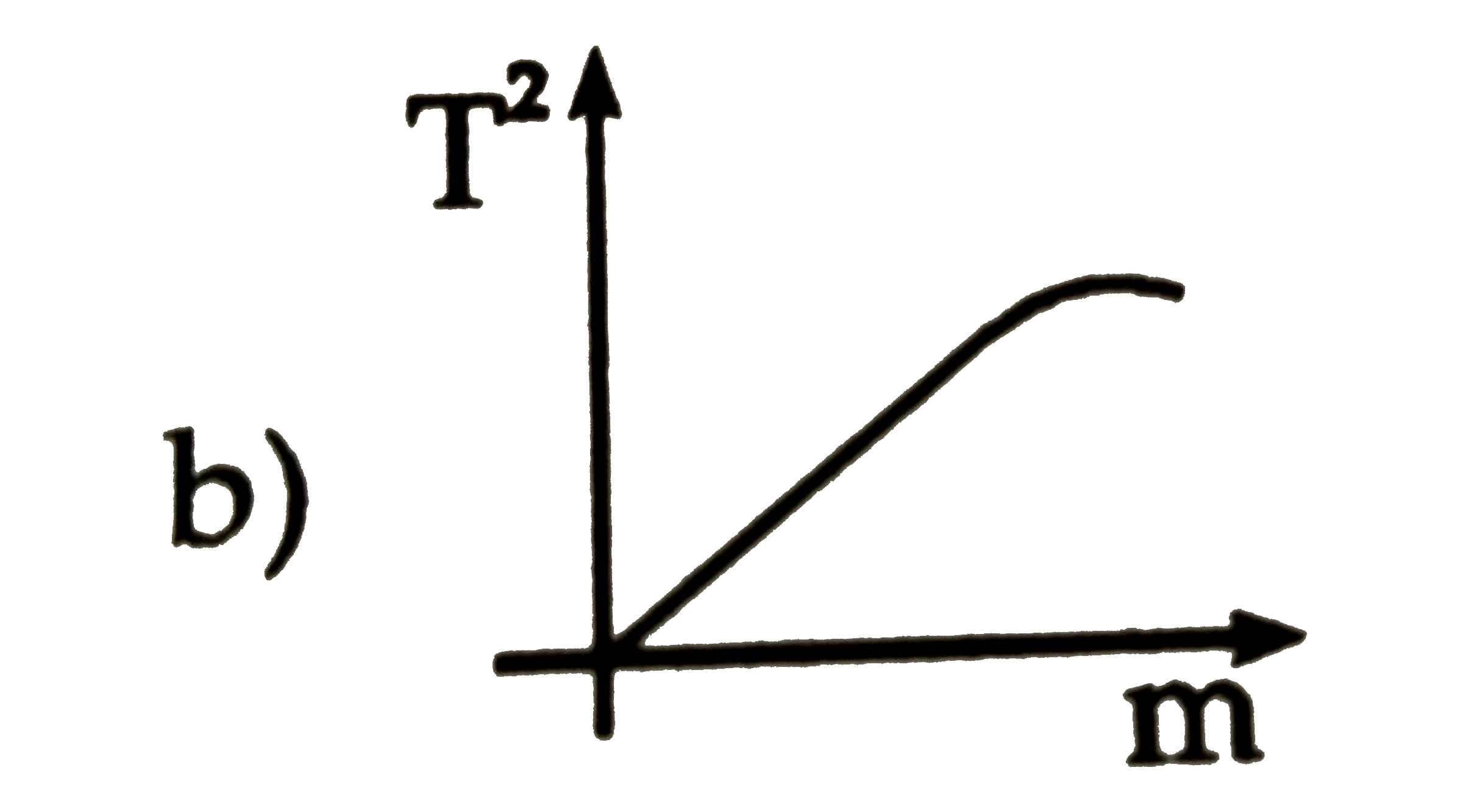 C
C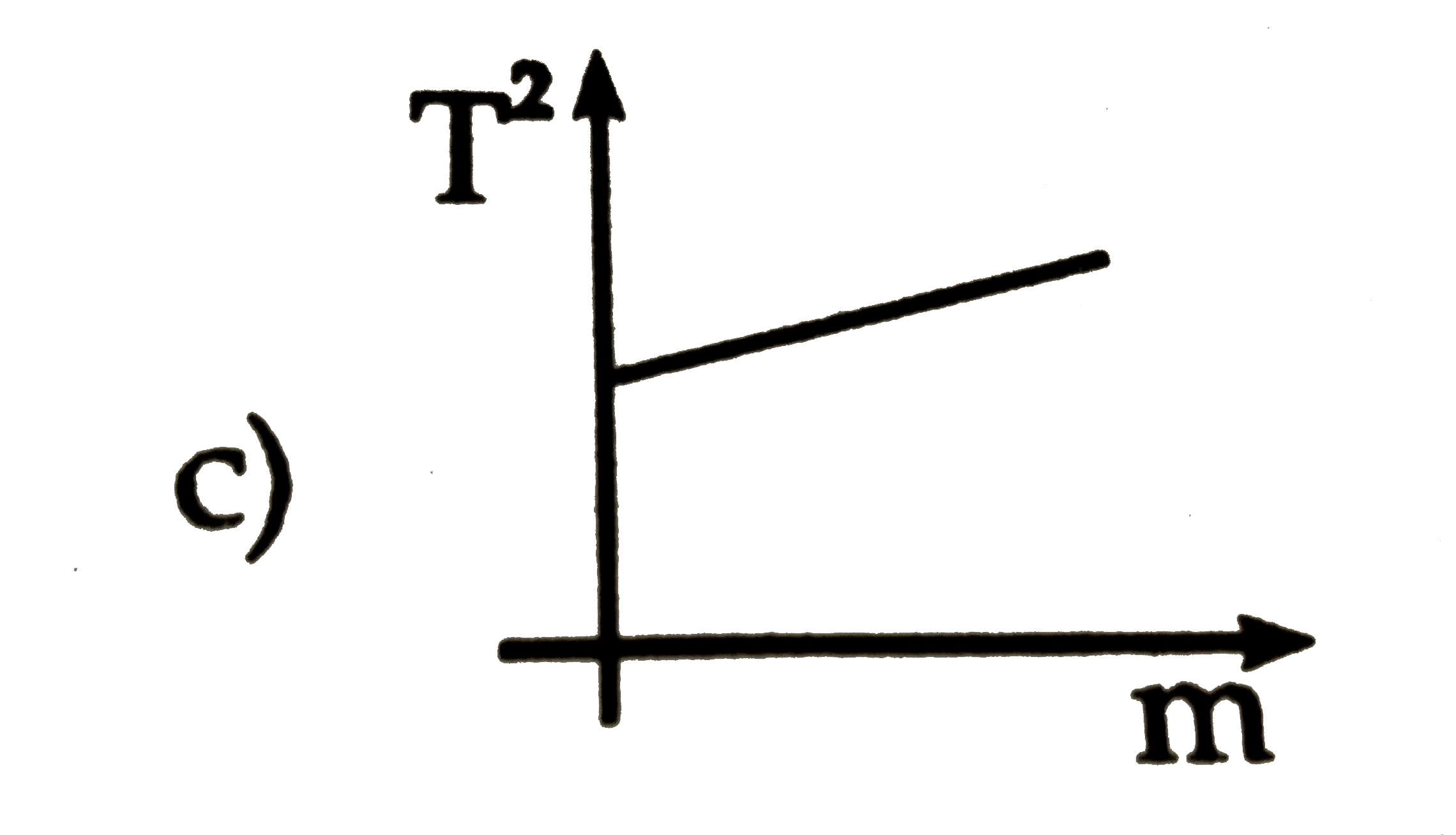 D
D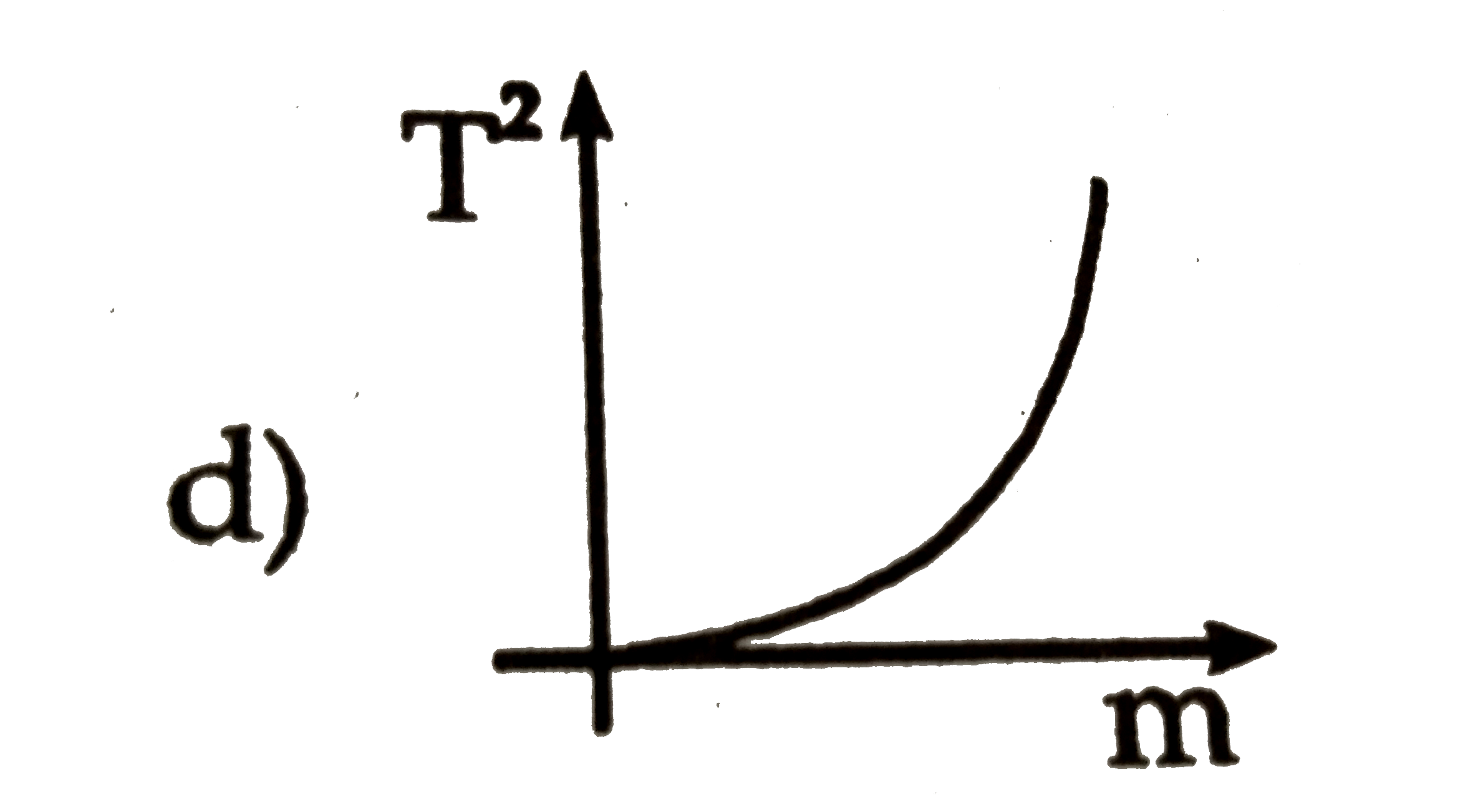
If a graph is plotted between ln k and 1/T for the first order reaction, the slope of the straight line so obtained is given by
A−EaRB−Ea2.303RC−2.303EaRD−Ea2.303If a graph is plotted between log(a−x) and t, the slope of the straight line is equal to −0.03. The specific reaction rate will be
A6.9×10−2B6.9C0.69D6.9×10−4
For a first order reaction, when a graph is plotted between log10([A])0([A])t on y-axis and time (t) on x-axis , slope of the graph of the graph is equal to __________.
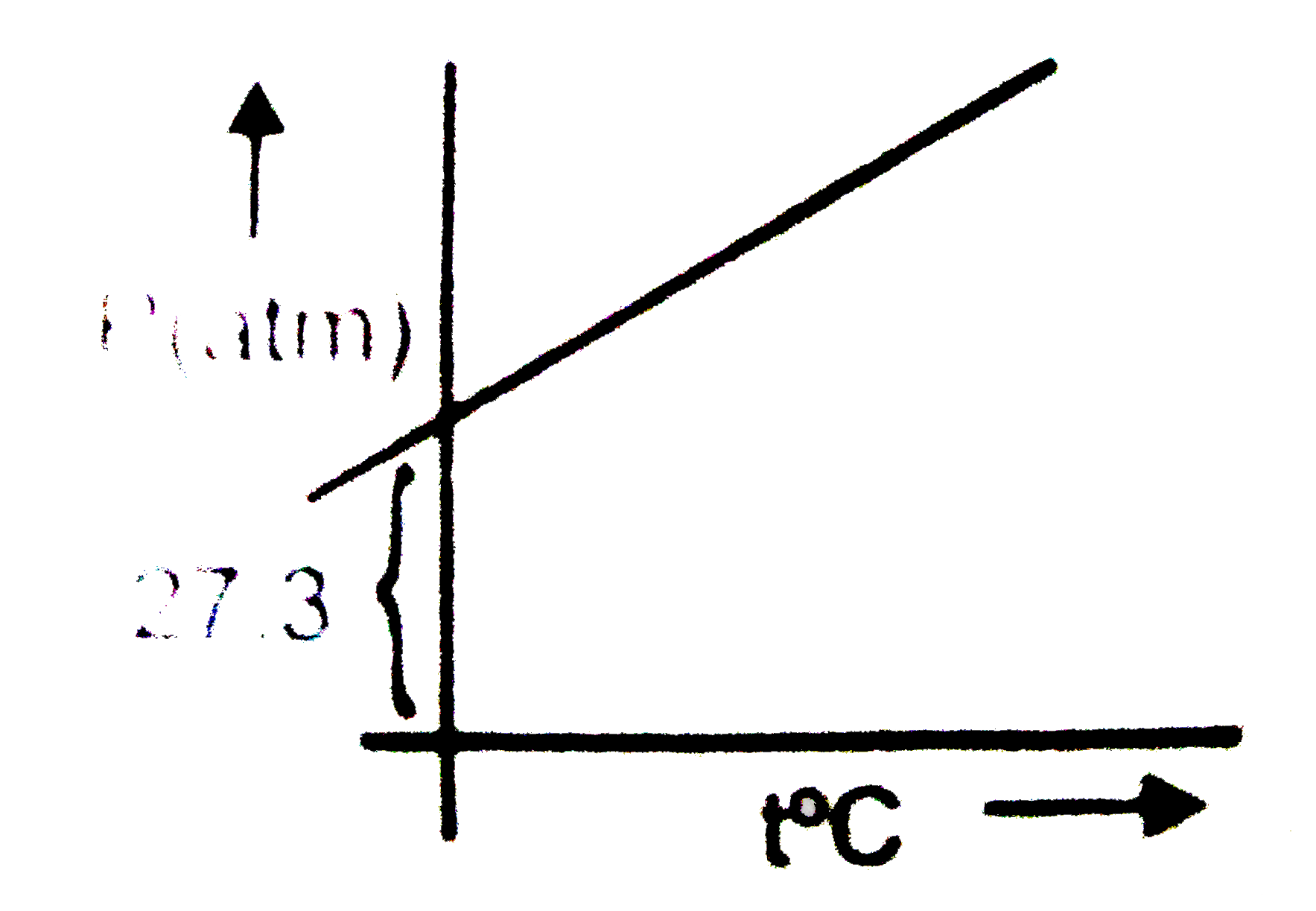
View SolutionA graph is plotted between p (atm) vs t∘C for 10 mol of an ideal gas as follows:
Then slope of curve and volume of container (L) respectively, are:
View SolutionFor a planet, the graph of T2 against r3 is plotted. The slope of the graph is
View SolutionKepler's third law states that the square of period of revolution (T) of a planet around the sun, is proportional to third power of average distance, r between the sun and the planet i.e.
T2=Kr3
Here, K is constant.
If masses of the sun and the planet are M and m respectively, then as per Newton's law of gravitation, force of attraction between them is F=GMmr2 where G is gravitational constant.The relation between G and K is described as
View SolutionKeller's third law states that the square of period of revolution (T) of a planet around the sun is proportional to the sun is proportional to the third power of average distance , r between the sun and the planet i.e T2=Kr3 Here ,K is constant . If masses of the sun and the planet are M and m respectively , then as per Newton's law of gravitation force of attraction between them is F=GMmr2 , Where G is gravitational constant . The relation between G and K is described as
View Solution

