Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
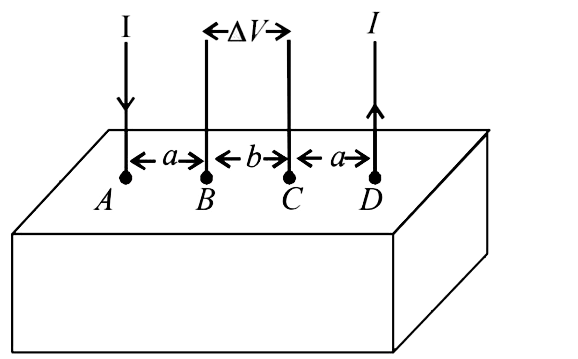
For current entering at A, the electric field at a distance 'r'
rhiI8πr2
rhiIr2
rhiI2πr2
rhiI4πr2
Step by step video & image solution for Consider a block of conducting material of resistivity 'rho' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage DeltaV developed between 'B' and 'C'. The calculation is done in the following steps: (i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block. (ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E = rhoj, where j is the current per unit area at 'r'. (iii) From the 'r' dependence of E(r), obtain the potential V(r) at r. (iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'. For current entering at A, the electric field at a distance 'r' by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
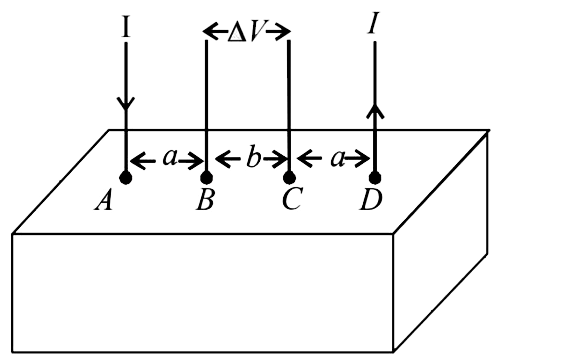
Delta V measured between B and C isAρIπa−ρIπ(a+b)BρIa−ρIa+bCρI2πa−ρI2π(a+b)DρI2π(a−b)When some potential differece is maintained between A and B, current I enters the network at A and leaves at B
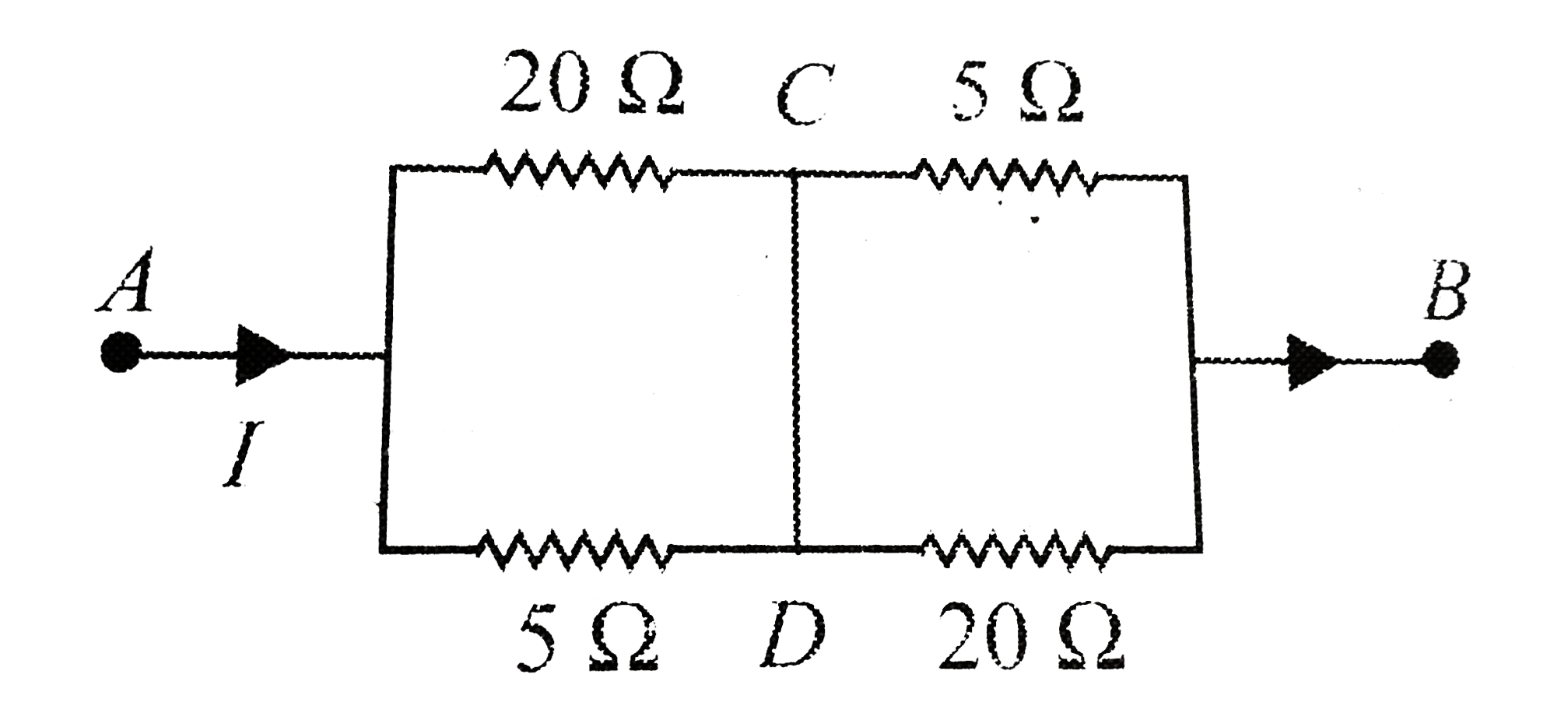 AThe equivalent resistance between A and B is 8Ω.BC and D are at the same potential.CNo current flows between C and D.DCurrent 3I/5 flows from D to C.
AThe equivalent resistance between A and B is 8Ω.BC and D are at the same potential.CNo current flows between C and D.DCurrent 3I/5 flows from D to C.A current carrying wire is placed in the grooves of an insulating semicircular disc of radius 'R', as shown in Fig. The current enters at point A and leaves from point B. Determine the magnetic field at Point D.
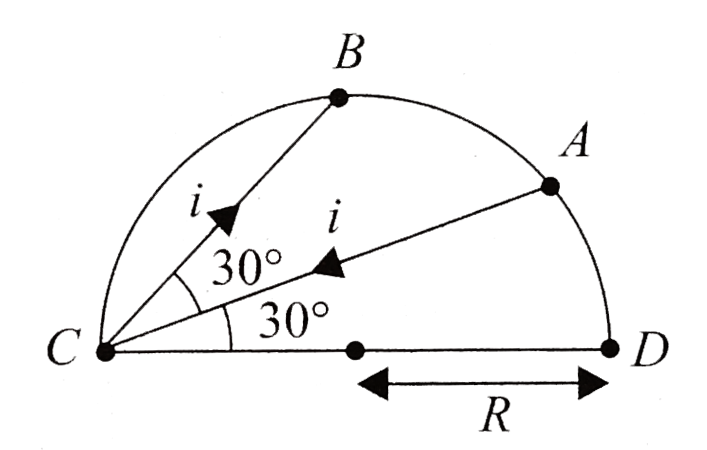 Aμ0i8πR√3Bμ0i4πR√3C√3μ0i8πRDNone of these
Aμ0i8πR√3Bμ0i4πR√3C√3μ0i8πRDNone of these
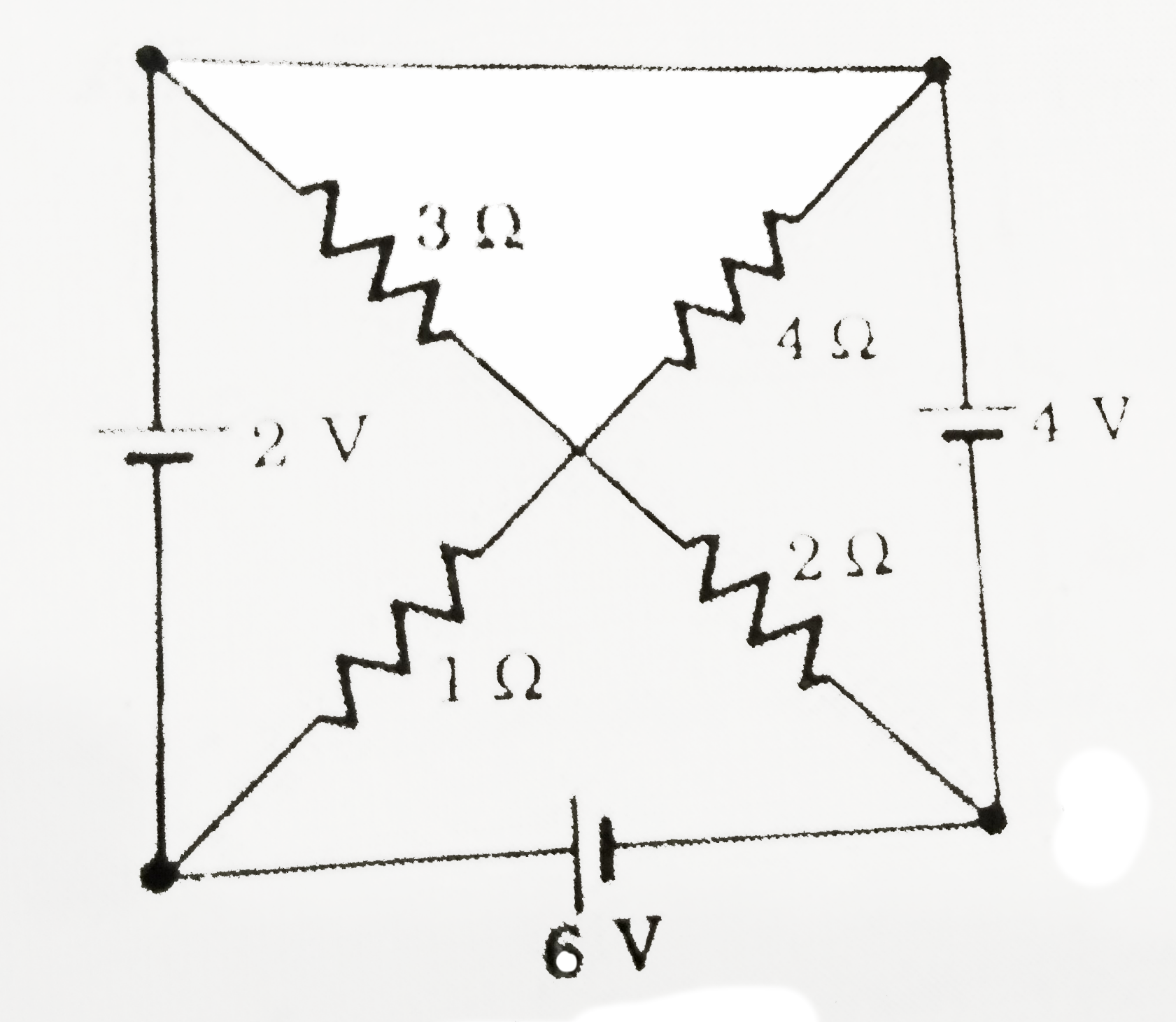
In the network shown in figure. (i) calculate the current of the 6V battery and (ii) determine the potential difference between the points A and B.
View SolutionIn the circuit shown in figure a current I=600μA enters through A and leaves through B. Reading of the identical voltmeters V1andV2 are 20Vand30Vrespectively. find R.

View SolutionCalculate current (i) flowing in part of the circuit shown in figure?

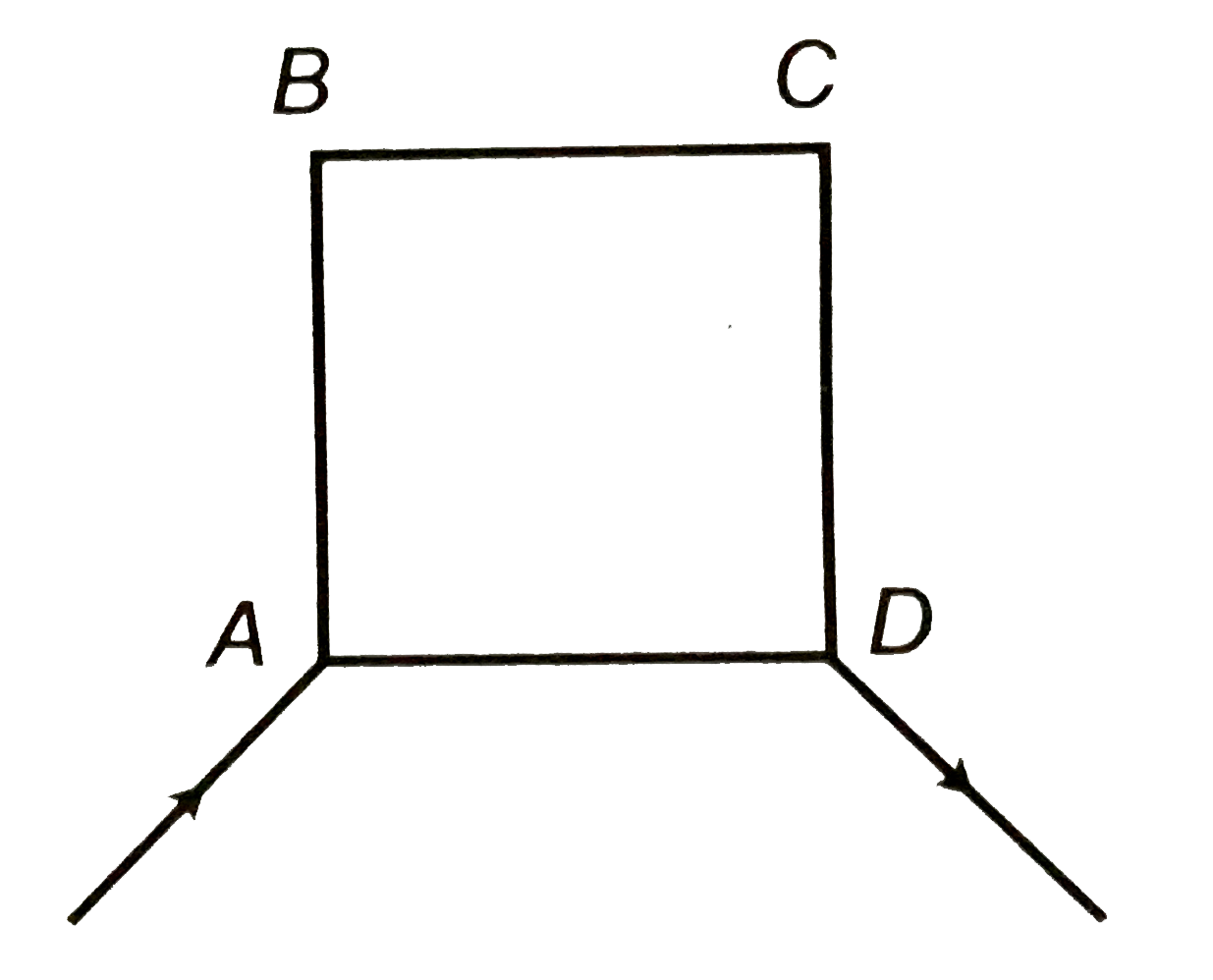
View SolutionABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
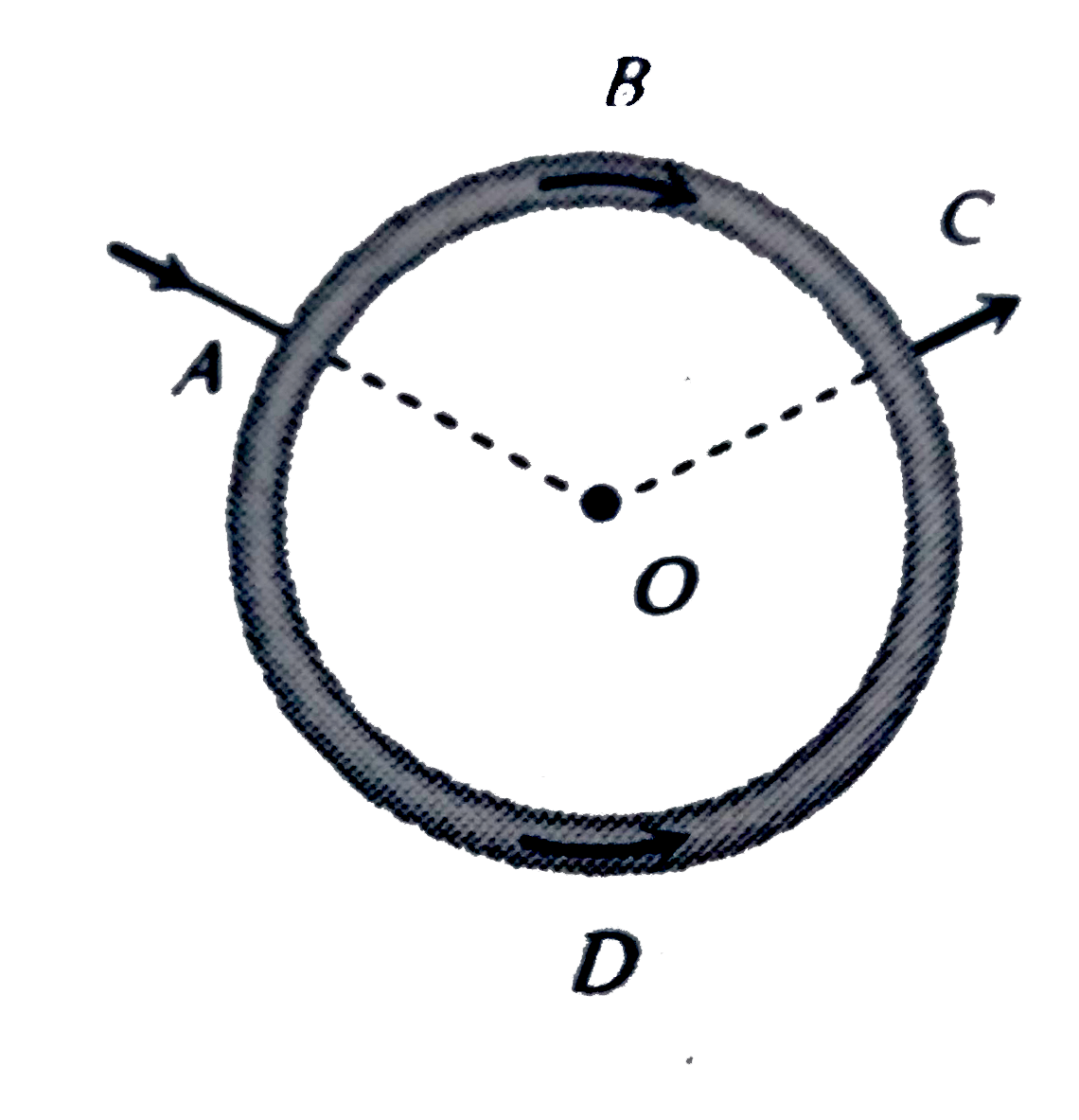
View SolutionA uniform wire is bent in the form of a circle of radius R. A current I enters at A and leaves at C as shown in the figure :
If the length ABC is half of the length ADC, the magnetic field at the centre O will be
View Solution


