A block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
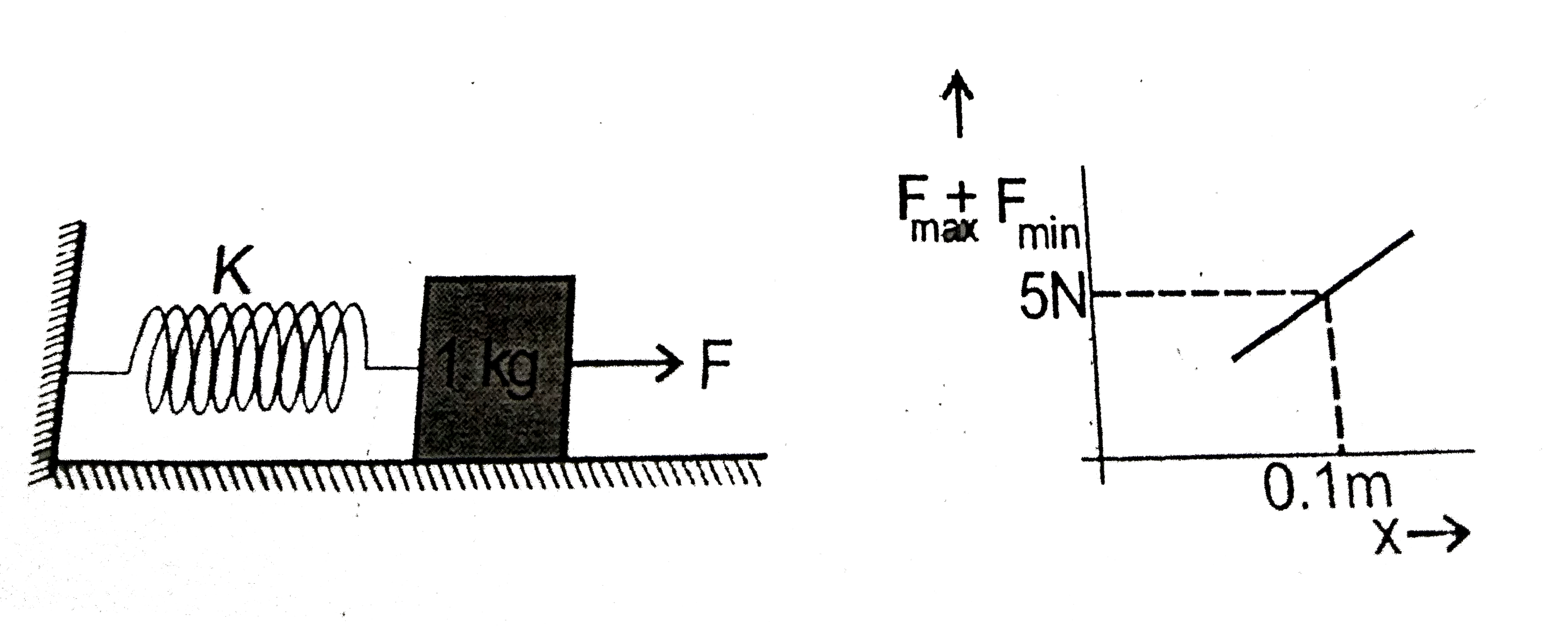
The coefficient of friction between the block and the horizontal surface is :
0.1
0.2
0.3
0.4
Step by step video & image solution for A block of mass 1kg is placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x ge (mumg)/(k)). Let F_(max) and F_(mi n) be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x, F_(max)-F_(mi n)=2N. Also shown is the variation of F_(max)+F_(mi n) versus x, the elongation of the spring. The coefficient of friction between the block and the horizontal surface is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

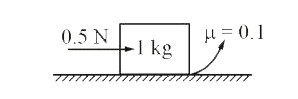
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
View Solution
Knowledge Check
A block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
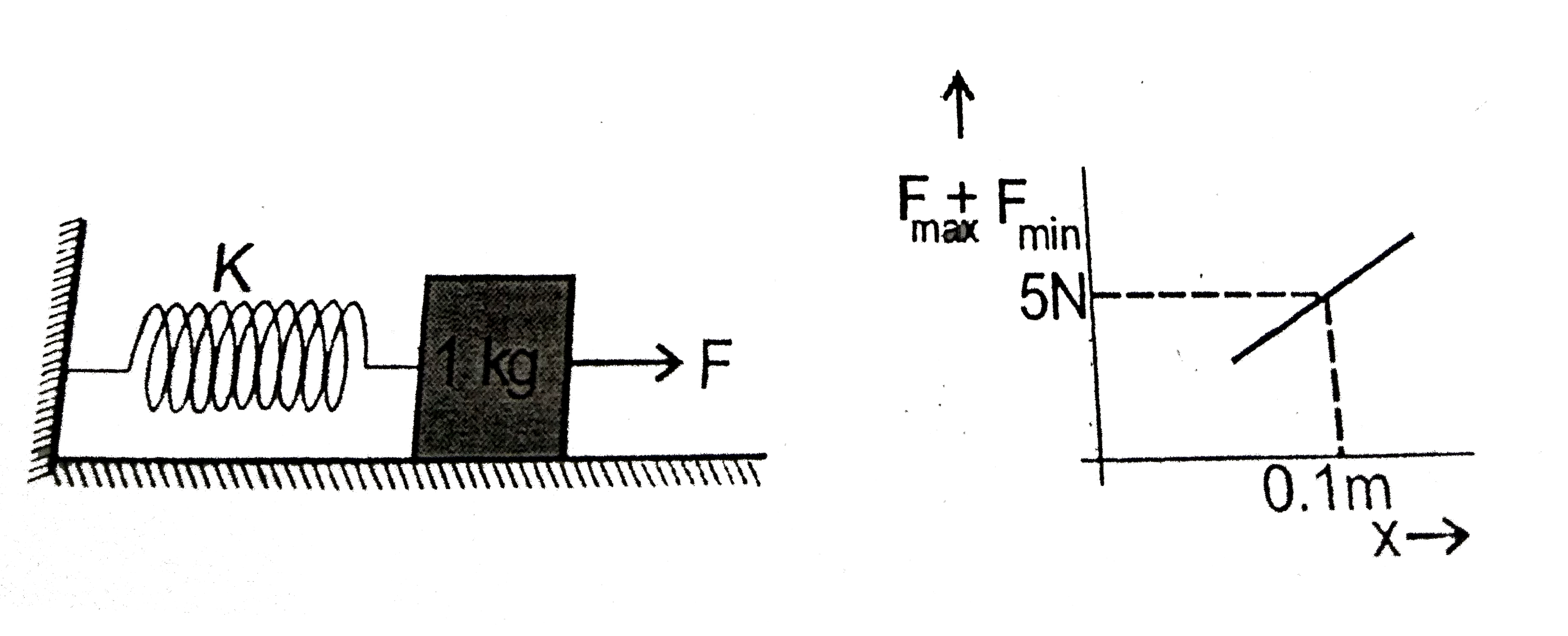
The value of Fmin, if x=3cm is :A0B0.2NC5ND1NA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
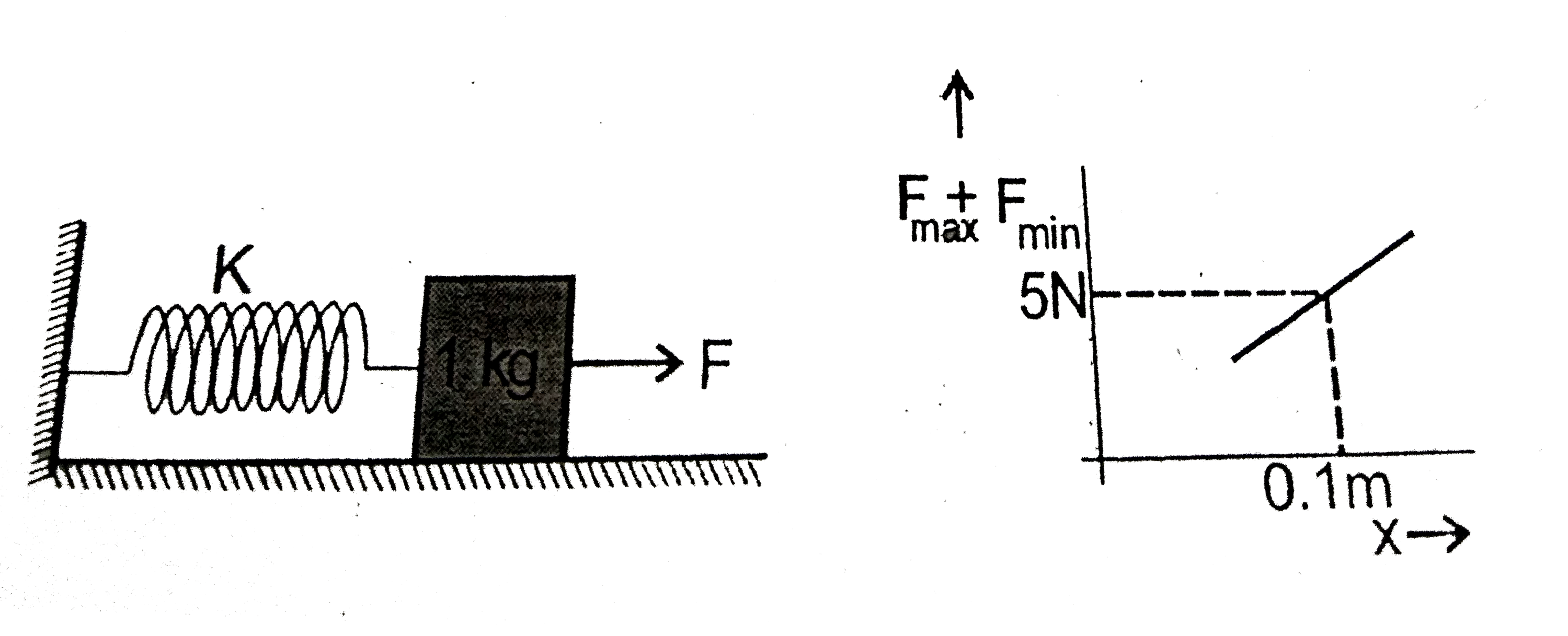
The spring constant of the spring is :A25N/mB20N/mC2.5N/mD50N/mA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 A1.0kgB0.1kgC2.0kgD0.2kg
A1.0kgB0.1kgC2.0kgD0.2kg
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionTwo blocks of equal mass 2 kg are placed on a rough horizontally surfaces as shown and a force F is applied on the upper block . The system is initially at rest . Find acceleration of the lower block in m/s2 .

View SolutionA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionIn previous question, if a horizontal force F=μmg/2 act on the block and the block remains stationary, then tension in string is.

View SolutionA block of mass 10 kg is placed on the rough horizontal surface. A pulling force F is acting on the block which makes an angle θ above the horizontal. If coefficient of friction between block and surface is 43 then minimum value of force required to just move the block is (g=10ms2)
View Solution

