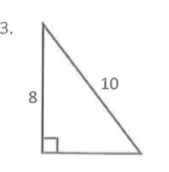
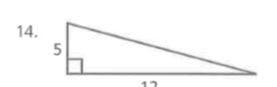
A triangle with side lengths of 5, 12, and 15 centimeters is similar to another triangle. The longest side of the other triangle has length 24 centimeters. What is the perimeter, in centimeters, of the triangle?
38.4
44
51.2
58
The correct Answer is:C
To solve the problem step by step, we will follow the reasoning presented in the video transcript.
Step 1: Identify the sides of the given triangle.
The sides of the first triangle are:
- Side 1: 5 cm
- Side 2: 12 cm
- Side 3 (longest side): 15 cm
Step 2: Identify the longest side of the second triangle.
The longest side of the second triangle is given as 24 cm.
Step 3: Set up the ratio of the sides of the triangles.
Since the triangles are similar, the ratio of the corresponding sides will be the same. We can set up the ratio of the longest sides:
1524
Step 4: Simplify the ratio.
To simplify the ratio:
1524=58
This means that the sides of the second triangle are in the ratio of 5:8 compared to the first triangle.
Step 5: Find the lengths of the other sides of the second triangle.
Using the ratio 58, we can find the lengths of the other sides of the second triangle.
For the shortest side:
Let x be the length of the shortest side in the second triangle. Using the ratio:
5x=58
Cross-multiplying gives:
5⋅8=5⋅x⟹40=5x⟹x=405=8 cm
For the middle side:
Let y be the length of the middle side in the second triangle. Using the ratio:
12y=58
Cross-multiplying gives:
12⋅8=5⋅y⟹96=5y⟹y=965=19.2 cm
Step 6: List the sides of the second triangle.
Now we have all the sides of the second triangle:
- Shortest side: 8 cm
- Middle side: 19.2 cm
- Longest side: 24 cm
Step 7: Calculate the perimeter of the second triangle.
The perimeter P of the triangle is the sum of its sides:
P=24+19.2+8
Calculating this gives:
P=51.2 cm
Final Answer:
The perimeter of the triangle is 51.2 cm.
---
The sides of the first triangle are:
- Side 1: 5 cm
- Side 2: 12 cm
- Side 3 (longest side): 15 cm
The longest side of the second triangle is given as 24 cm.
Since the triangles are similar, the ratio of the corresponding sides will be the same. We can set up the ratio of the longest sides:
1524
To simplify the ratio:
1524=58
This means that the sides of the second triangle are in the ratio of 5:8 compared to the first triangle.
Using the ratio 58, we can find the lengths of the other sides of the second triangle.
Let x be the length of the shortest side in the second triangle. Using the ratio:
5x=58
Cross-multiplying gives:
5⋅8=5⋅x⟹40=5x⟹x=405=8 cm
Let y be the length of the middle side in the second triangle. Using the ratio:
12y=58
Cross-multiplying gives:
12⋅8=5⋅y⟹96=5y⟹y=965=19.2 cm
Now we have all the sides of the second triangle:
- Shortest side: 8 cm
- Middle side: 19.2 cm
- Longest side: 24 cm
The perimeter P of the triangle is the sum of its sides:
P=24+19.2+8
Calculating this gives:
P=51.2 cm
The perimeter of the triangle is 51.2 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the triangle below , the lengths of the two given sides are measured in centimeters. What is the value , in centimeters, of x ?
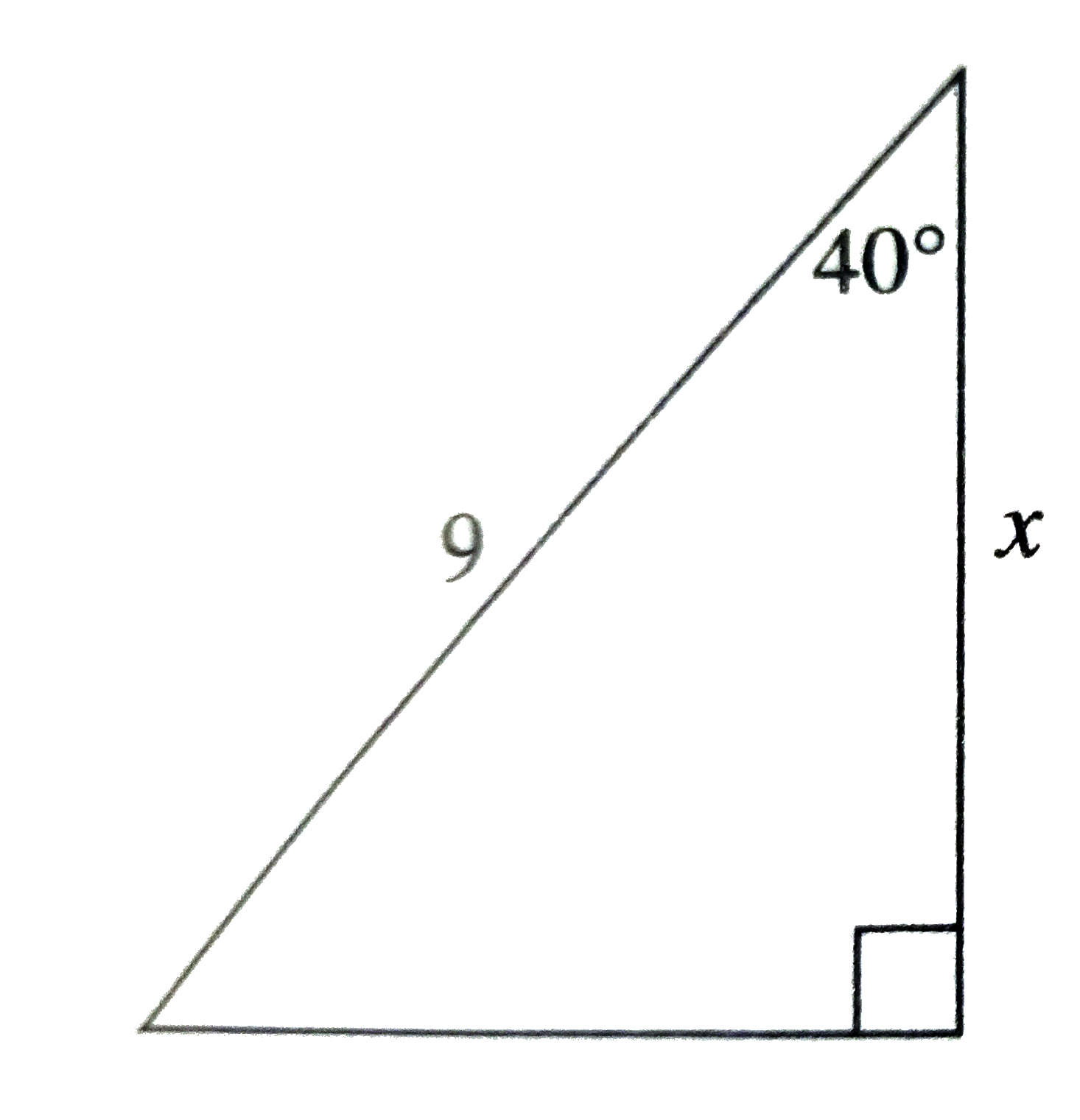 A9sin40∘B9sin50∘C9cos50∘D9tan40∘
A9sin40∘B9sin50∘C9cos50∘D9tan40∘ - Question 2 - Select One
Two similar triangles have perimeters in the ratio 3:5. The sides of the smaller triangle measure 3 cm, 5 cm, and 7 cmd, respectively. What is the perimeter, in centimeters, of the larger triangle?
A15B18C20D25 - Question 3 - Select One
AD is the longest side of the triangle ABD shown in the figure. What is the length side of ΔABC ?
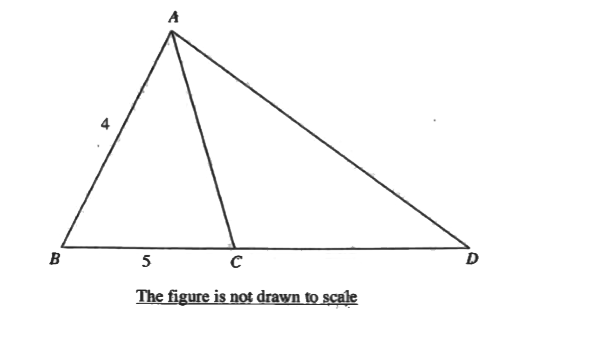 A2B3C√41D9
A2B3C√41D9
A triangle with integral sides has perimeter 8 cm. Then find the area of the triangle
View SolutionIf the length of two sides of an isosceles triangle are 3 and 7, what is the perimeter of the triangle?
View SolutionThe sides of a triangle are in the ratio 5 : 12 : 13 and its perimeter is 150 cm. Find the area of the triangle.
View SolutionIn the figure below, △ABCand△DEF are similar triangles with the given side lengths in meters. What is the perimeter, in meters, of △DEF ?
 View Solution
View SolutionIf the longer leg of a right triangle has length 32 centimeters, and the measure of the angle that is adjacent to that leg is 30∘, which of the following represents the length, in centimeters , of the hypotenuse of the triangle?
View Solution