The most popular items at a bakery are its raspberry scones and its lemon poppy seed muffins. The shop sells both items in boxes of 12 at a cost of $15 per box of raspberry scones and $9 per box of lemon poppy seed muffins. On Friday and Saturday, the shop earned $396 by selliing a total of 46 boxes of these two items. If r and l represent the number of boxes of raspberry scones and lemon poppy seed muffins sold over the two-day period, respectively, which of the following systems of equations could be used to find the number of boxes of each type of item sold?
r+l=46
15r+9l=396
r+l=12×46
15r+9l=396
r+l=46
15r+9l=3962
r+l=12×46
15r+9l=39612
The correct Answer is:A
Difficult: Medium
Category: Heart of Algebra/ System of Linear Equations
Strategic Advice: In a lengthy word problem that contains lots of numbers, it may help to cross out information that does not impact the answer.
Getting to the Answer: Here, the number of items in each box does not matter because the entire questions is about the boxes of items (not the number of items), so cross out the 12. This means you can eliminate B and D right away. The question states that r and l represent the number of boxes of raspberry scones and lemon poppy seed muffins sold and that the shop sold a total of 46 boxes of these items, so the first equations will be r+l=46. The shop collects $15 for each boc of raspbarry scones, which translates to 15r, and $9 for each box of lemon poppy seed muffins, which becomes 9l. Put together,the second equation is 15r+9l=396, making (A) the correct answer. Note that because the question doesn't ask about the number sold per day, you don't need to incorporate a 2 into either equation.
Topper's Solved these Questions
Similar Questions
The lateral area of the right circular cone is 60π. If the radius of the base is 6, what is the volume of the cone
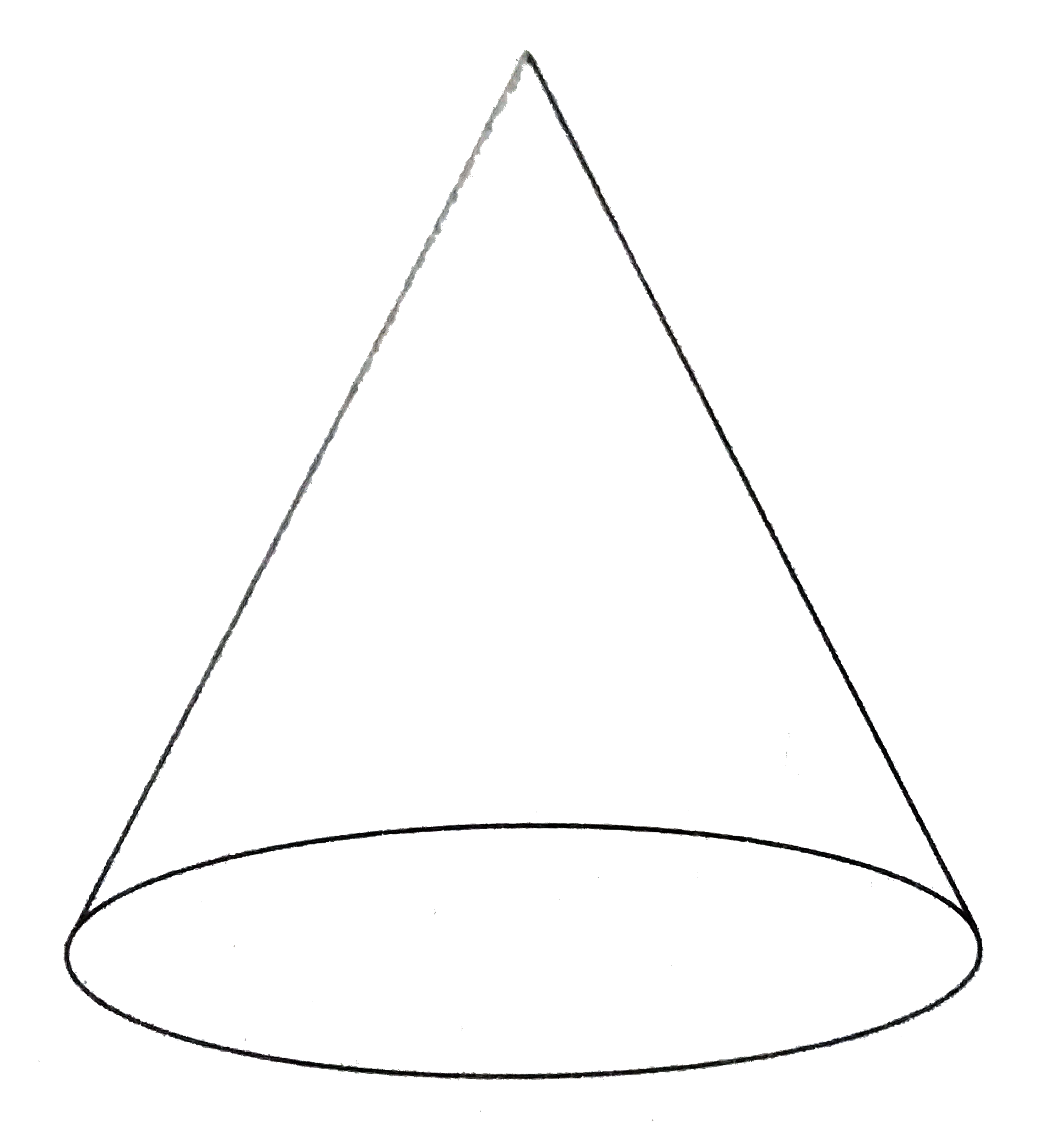
View SolutionIf x≠±1, then x+1x−1−x−1x+1=
View Solutionn - भिन्न वस्तुओं को दो भिन्न बॉक्स में रखने की विधियाँ ज्ञात कीजिए ताकि कोई भी बॉक्स रिक्त न रहे ।
View Solutionदो बक्सों में अलग-अलग तरह की वस्तुएँ कितने प्रकार से रखी जा सकती है यदि कोई भी बक्सा खाली न हों ?
View SolutionAred box contains eight itmes, of which three are defective, and a blue box contains five
itmes, of which two are defective. An item is drawn at random from each box. What is the
probability that both items will be nondefective?
View SolutionA red box contains eight items , of which three are defective, and a blue box contains five items, of which two are defective . An item is drawn at random from each box. What is the probability that one item is defective and one is not ?
View SolutionCarrie's Chocolate shop and Tamika's Treat Shop both sell cadny in boxes. The table below lists the price (the total amount the customer pays) of each box of candy sold at the shops. For each shop, there is a linear relationship between the price of a box of candies and the number of candies in the box. These are the only numbers of candies that can be purchased at the shops.

At Tamika's Treat Shop. What is the average price per candy in a box of 20, to the nearest $0.01 ?
View SolutionCarrie's Chocolate shop and Tamika's Treat Shop both sell cadny in boxes. The table below lists the price (the total amount the customer pays) of each box of candy sold at the shops. For each shop, there is a linear relationship between the price of a box of candies and the number of candies in the box. These are the only numbers of candies that can be purchased at the shops.

Which of the following equation gives the relationship between the price in dollars , c, and the number of candies ,n, in a box of cadies at carrie's chocolate shop ?
View Solutionएक फल विक्रेता सेब और सन्तरे खरीदने में ₹ 500 की पूँजी लगा सकता है। उसकी दुकान में फलों की केवल 12 पेटियाँ ही रखी जा सकती हैं। सेब की एक पेटी ₹ 50 और सन्तरे की एक पेटी ₹ 25 की आती है। वह सेब की प्रति पेटी ₹ 10 तथा सन्तरे की प्रति पेटी ₹ 6 के लाभ से बेचता है। यह मान कर कि वह खरीदी हुई सभी पेटियों को बेच सकता है, रैखिक प्रोग्रामन द्वारा ज्ञात एक कीजिए कि उसे सेब और सन्तरे की कितनी-कितनी पेटियाँ खरीदनी चाहिए ताकि उसे अधिकतम लाभ हो?
View SolutionThe average price per item in a shopping basket is $2.40. If there are a total of 30 items in the basket, what is the total price of the items in the basket ?
View Solutionएक फल विक्रेता सेब और सन्तरे खरीदने में ₹ 500 की पूँजी लगा सकता है। उसकी दुकान में फलों की केवल 12 पेटियाँ ही रखी जा सकती हैं। सेब की एक पेटी ₹ 50 और सन्तरे की एक पेटी ₹ 25 की आती है। वह सेब की प्रति पेटी ₹ 10 तथा सन्तरे की प्रति पेटी ₹ 6 के लाभ से बेचता है। यह मान कर कि वह खरीदी हुई सभी पेटियों को बेच सकता है, रैखिक प्रोग्रामन द्वारा ज्ञात एक कीजिए कि उसे सेब और सन्तरे की कितनी-कितनी पेटियाँ खरीदनी चाहिए ताकि उसे अधिकतम लाभ हो?
View Solutionएक फल विक्रेता सेब और सन्तरे खरीदने में ₹ 500 की पूँजी लगा सकता है। उसकी दुकान में फलों की केवल 12 पेटियाँ ही रखी जा सकती हैं। सेब की एक पेटी ₹ 50 और सन्तरे की एक पेटी ₹ 25 की आती है। वह सेब की प्रति पेटी ₹ 10 तथा सन्तरे की प्रति पेटी ₹ 6 के लाभ से बेचता है। यह मान कर कि वह खरीदी हुई सभी पेटियों को बेच सकता है, रैखिक प्रोग्रामन द्वारा ज्ञात एक कीजिए कि उसे सेब और सन्तरे की कितनी-कितनी पेटियाँ खरीदनी चाहिए ताकि उसे अधिकतम लाभ हो?
View SolutionThere are two confectioneries in a locality. The number of chocolate boxes in the first shop is 250 less than twice the number of chocolate boxes available in the second shop. By the end of the day, the first shop has sold 350 boxes and the second shop has sold 200 boxes. The number of boxes left unsold in both the shops is equal. Find the number of chocolates in both the shops at the beginning of the day.
View SolutionA stationery box has 15 pencils and 21 pens. Express in simplest form:
The ratio of number of pens to the total number of stationery items in the box
View SolutionComplete the table by selecting suitable items from the box:
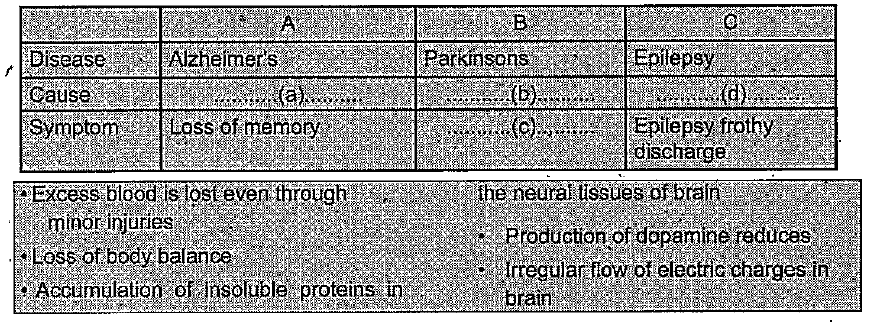
View Solution
