A triangle and a regular hexagon have the same perimeter. If the area of the hexagon is 72√3, what is the area of the triangle ?
62.354
83.138
101.823
103.923
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Area of the Hexagon
The area A of a regular hexagon can be calculated using the formula:
A=3√32s2
where s is the length of a side of the hexagon.
Step 2: Set Up the Equation
Given that the area of the hexagon is 72√3, we can set up the equation:
3√32s2=72√3
Step 3: Simplify the Equation
To simplify, we can divide both sides by √3:
32s2=72
Step 4: Solve for s2
Next, we multiply both sides by 23:
s2=72⋅23=48
Step 5: Find s
Now, take the square root of both sides to find s:
s=√48=4√3
Step 6: Calculate the Perimeter of the Hexagon
The perimeter P of the hexagon is given by:
P=6s=6⋅4√3=24√3
Step 7: Find the Side Length of the Triangle
Since the triangle has the same perimeter as the hexagon, the perimeter of the triangle is also 24√3. The perimeter P of a triangle with side length a is given by:
P=3a
Setting this equal to the perimeter of the hexagon:
3a=24√3
Solving for a:
a=24√33=8√3
Step 8: Calculate the Area of the Triangle
Now, we can find the area A of the triangle using the formula:
A=√34a2
Substituting a=8√3:
A=√34(8√3)2
Calculating (8√3)2:
(8√3)2=64⋅3=192
Now substituting back into the area formula:
A=√34⋅192=48√3
Final Answer
Thus, the area of the triangle is 48√3.
---
The area A of a regular hexagon can be calculated using the formula:
A=3√32s2
where s is the length of a side of the hexagon.
Given that the area of the hexagon is 72√3, we can set up the equation:
3√32s2=72√3
To simplify, we can divide both sides by √3:
32s2=72
Next, we multiply both sides by 23:
s2=72⋅23=48
Now, take the square root of both sides to find s:
s=√48=4√3
The perimeter P of the hexagon is given by:
P=6s=6⋅4√3=24√3
Since the triangle has the same perimeter as the hexagon, the perimeter of the triangle is also 24√3. The perimeter P of a triangle with side length a is given by:
P=3a
Setting this equal to the perimeter of the hexagon:
3a=24√3
Solving for a:
a=24√33=8√3
Now, we can find the area A of the triangle using the formula:
A=√34a2
Substituting a=8√3:
A=√34(8√3)2
Calculating (8√3)2:
(8√3)2=64⋅3=192
Now substituting back into the area formula:
A=√34⋅192=48√3
Thus, the area of the triangle is 48√3.
Topper's Solved these Questions
- PLANE GEOMETRY Book:KAPLANChapter:PLANE GEOMETRY Exercise:PLANE GEOMETRY FOLLOW - UP TEST
Explore 6 Videos
- MISCELLANEOUS TOPICS Book:KAPLANChapter:MISCELLANEOUS TOPICS Exercise:MISCELLANEOUS TOPICS FOLLOW - UP TEST
Explore 12 Videos
- PRACTICE TEST 1 Book:KAPLANChapter:PRACTICE TEST 1 Exercise:PRACTICE TEST
Explore 50 Videos
Similar Questions
Knowledge Check

If x=3, what is the area of the triangle above?A10B21C30D45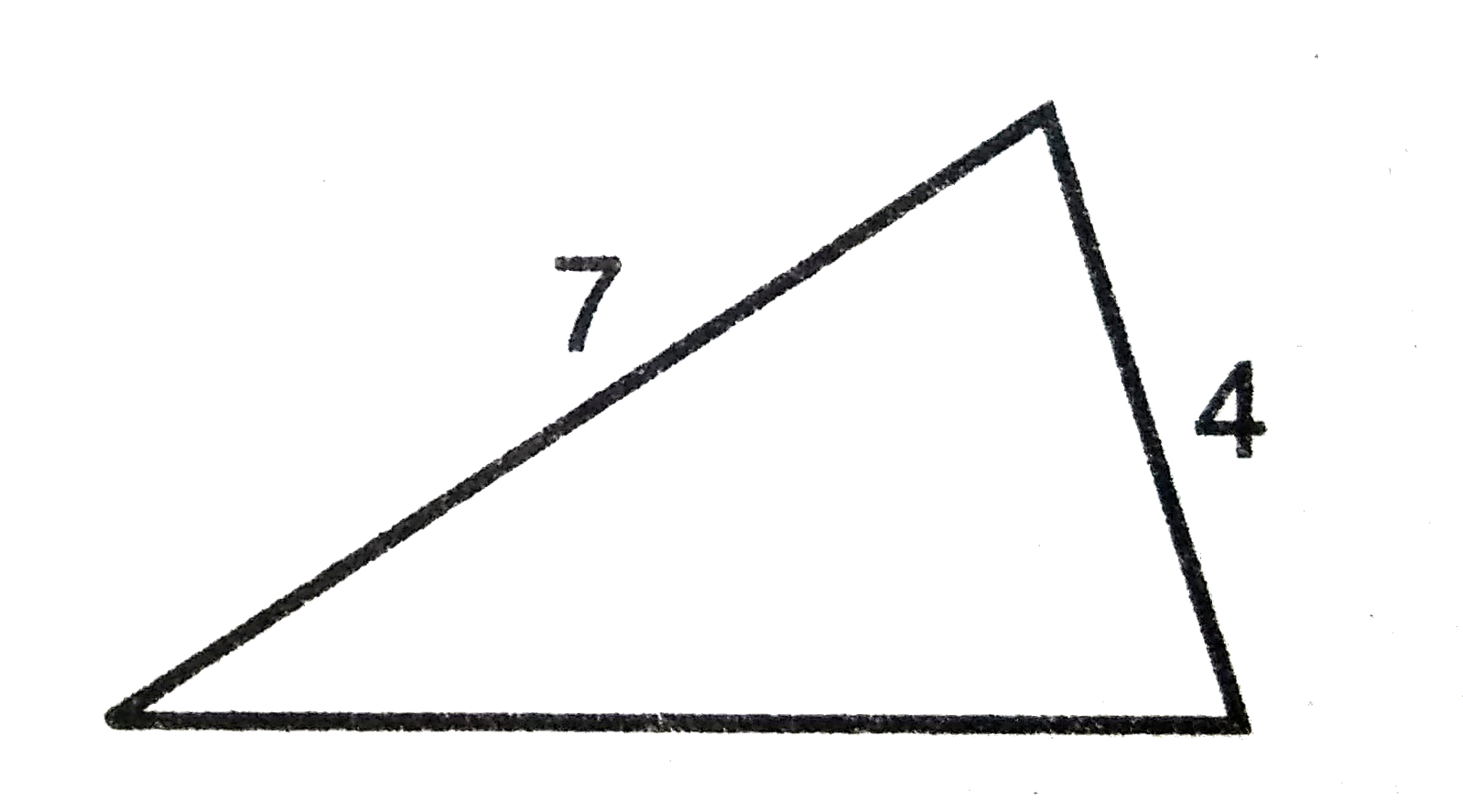
If the perimeter above is 18, what is the area of the triangle?A2√33B6√5C14D9√5
The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384 √3 square inches, what is the area, in square inches, of the square?A256B192C64√3D16√3
A regular hexagon is inscribed the circle. If the area of hexagon is 24√3 cm2 , find the area of the circle. (Use π=3.14)
View SolutionIf ¯¯¯¯¯¯XY=3, what is the area of ΔXYZ ?
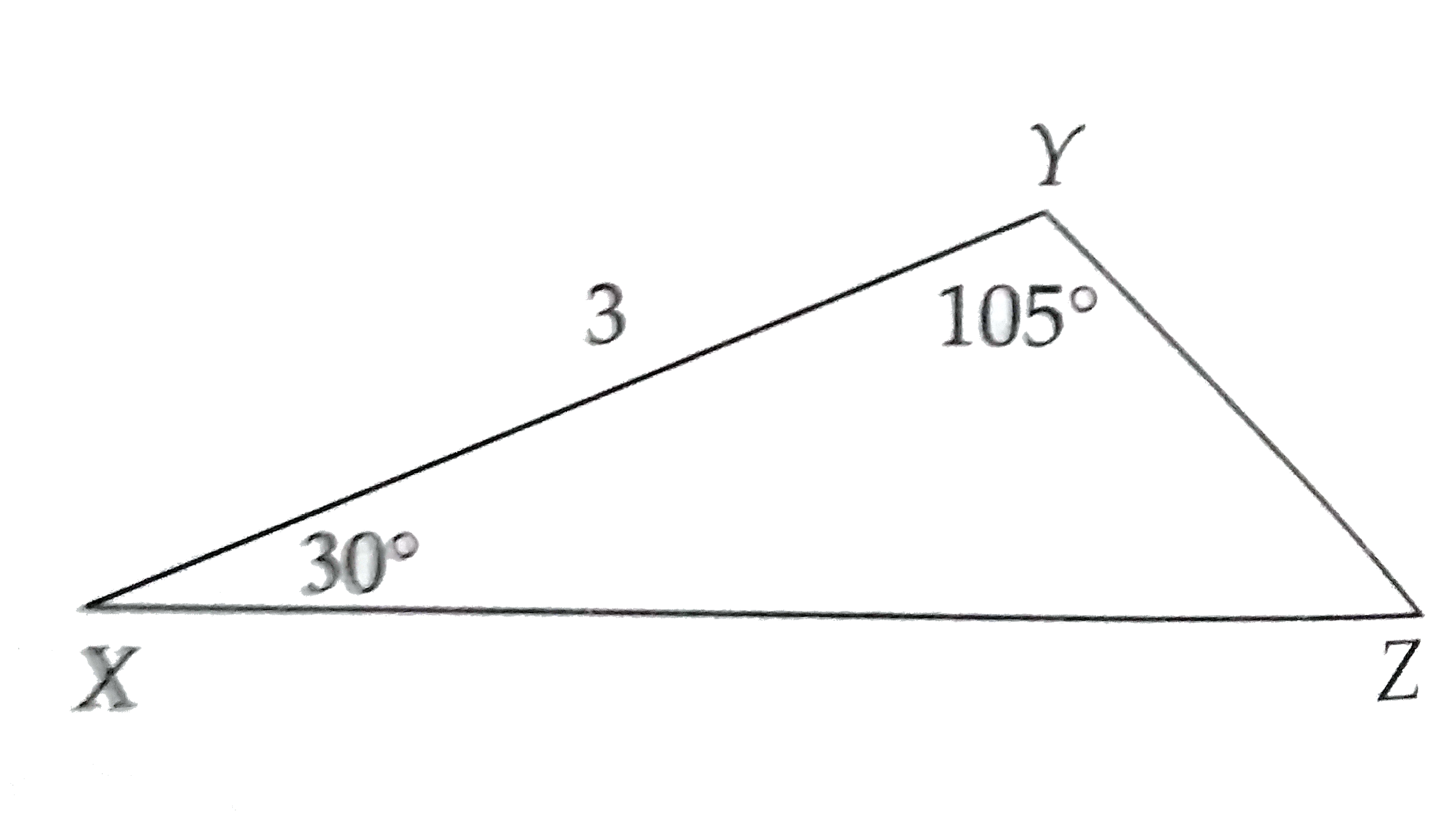
View SolutionA triangle with integral sides has perimeter 8 cm. Then find the area of the triangle
View SolutionIf the area of an equilateral triangle is 16√3cm2, then the perimeter of the triangle is
View Solution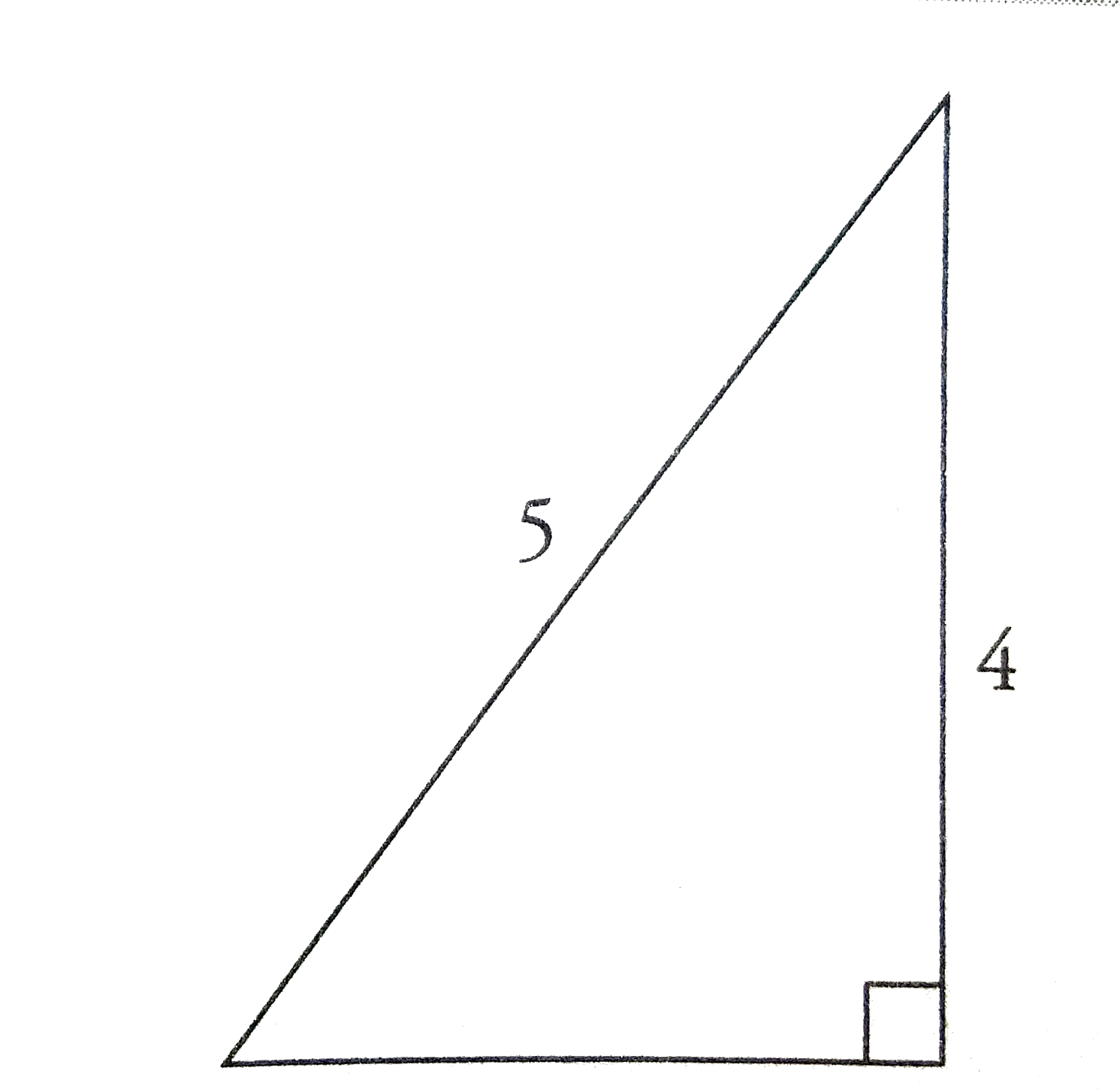
If the area of the triangle above is 6, what is its perimeter?
View Solution

