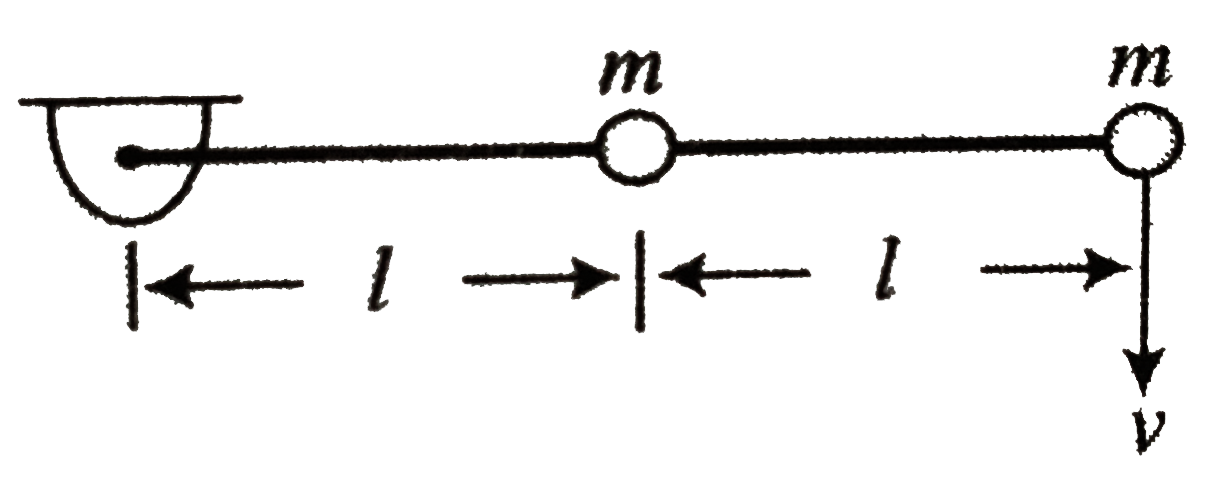
A large number (n) of identical beads, each of mass m and radius r are strung on a thin smooth rigid horizontal rod of length $L (L > > r)$ an dare at rest at random positions. The rod is mounted between two rigid supports (see figure). If one of the beads is now given a speed v, the average force experienced by each support after a lone time is (assume all collision are elastic) :-

A

$\frac{m v^{2}}{2 (L - n r)}$

B

$\frac{m v^{2}}{L - n r}$

C

zero

D

$\frac{m v^{2}}{L - 2 n r}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Change In momentum in each collision with rigid support $Δ P = 2 m v$
time gap between two successive collision with same support $Δ t = \frac{2 L - 4 n r}{v}$
$F_{ave} = \frac{Δ P}{Δ t}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Five identical balls each of mass m and radius r are string like beads at random and at rest along a smooth rigid horizontal thin rod of length L mounted between immovable supports Assume $10 r \leq L$ and that the collision between balls or between balls and supports are elastic if one ball is struck horizontally so as to acquire a speed v the average force felt by the support is

A $\frac{5 m v^{2}}{L - 5 r}$
B $\frac{m v^{2}}{L - 10 r}$
C $\frac{5 m v^{2}}{L - 10 r}$
D $\frac{m v^{2}}{L - 5 r}$
Question 2 - Select One
Three identical rods, each of mass $m$ and length $l$ , form an equaliteral triangle. Moment of inertia about one of the sides is

A $\frac{m l^{2}}{6}$
B $m l^{2}$
C $\frac{3 m l^{2}}{4}$
D $\frac{2 m l^{2}}{3}$
Question 3 - Select One
Two masses each of mass $M$ are attached to the end of a rigid massless rod of length $L$ . The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
A $\frac{M L^{2}}{4}$
B $\frac{M L^{2}}{2}$
C $M L^{2}$
D $2 M L^{2}$

ALLEN-CENTRE OF MASS-EXERCISE-V A

Home
Ask Doubt
Profile