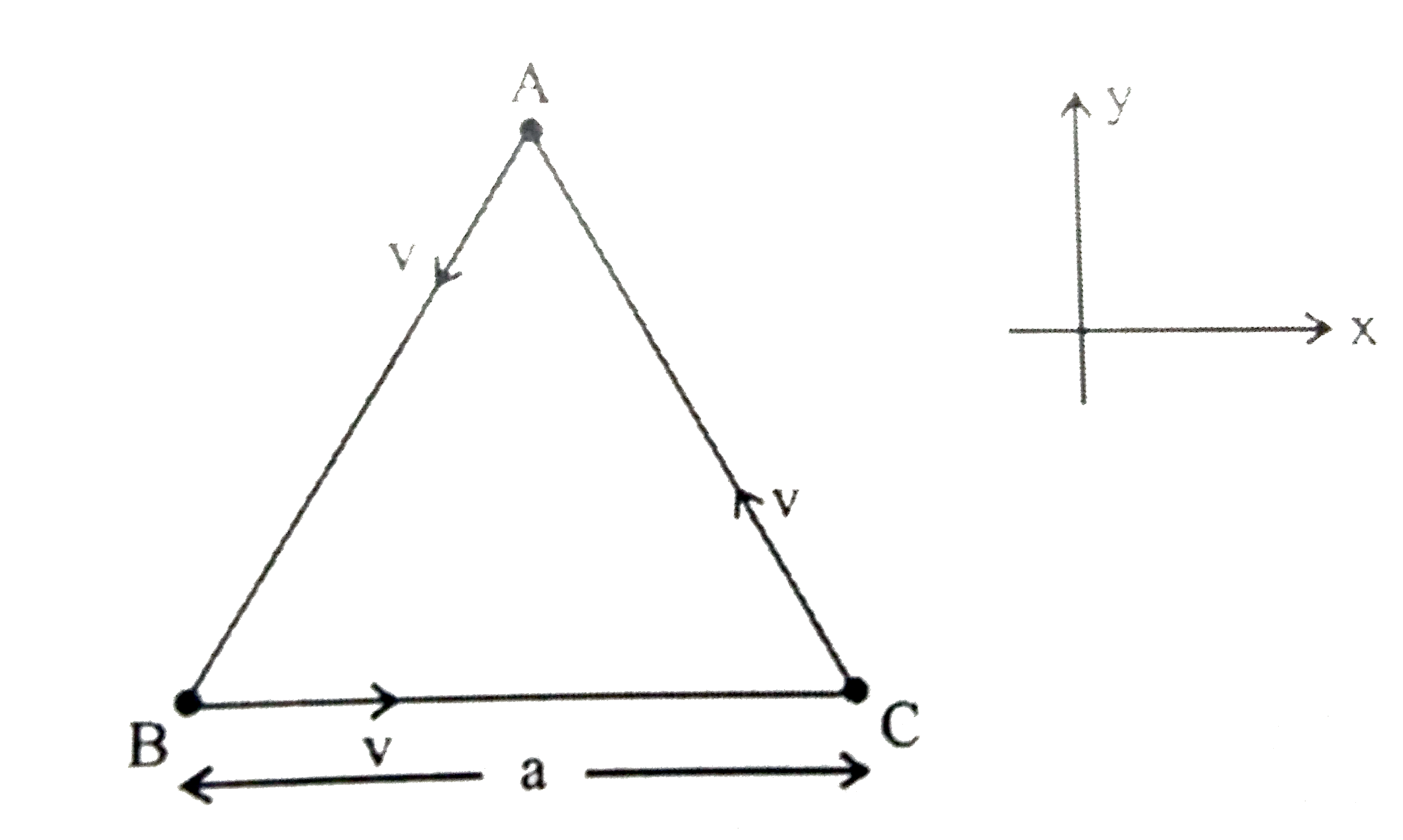
Three particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
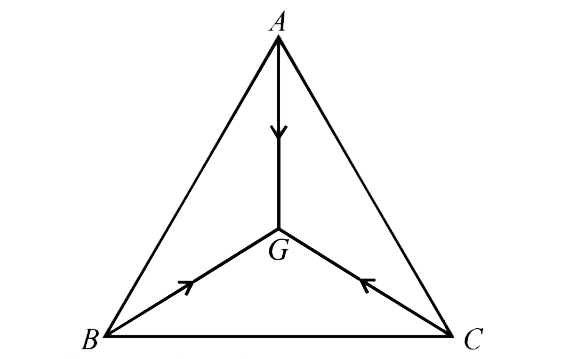
The correct Answer is:→vc=−→vB
COLM : implies that →vC & →vB are opposite to each other.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Three particlesA,B and C of equal mass move with equal speed V=5ms−1 along the medians of an equilateral triangle as shown in the figure. They collide at the centroid G of the triangle. After the collision, A comes to rest, B retraces its path with the speed V=5ms−1. What is the speed of C?
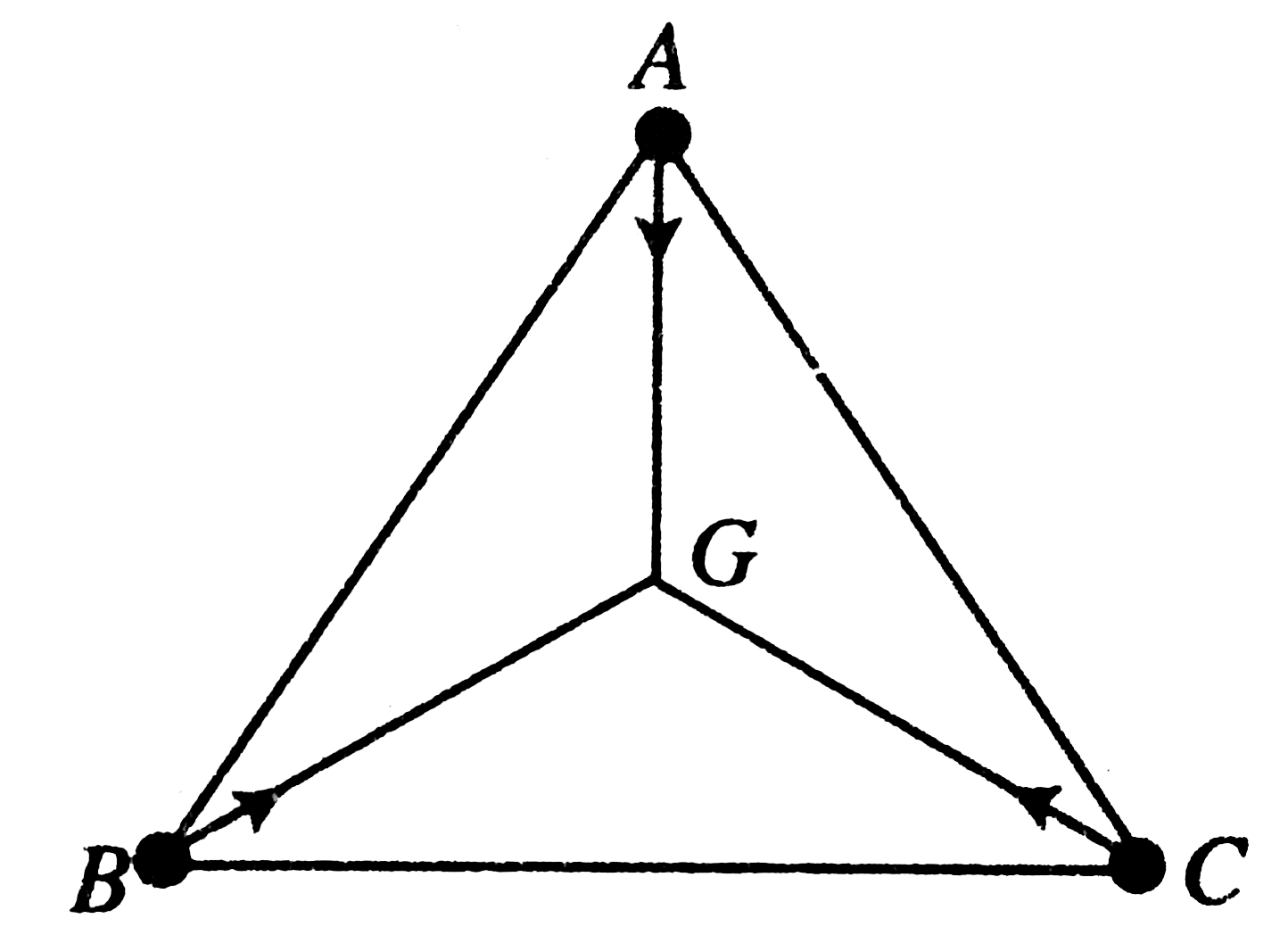
View SolutionThree particles of equal masses are initial at the vertices of equilateral triangle of side 2√3m in horizontal plane. They start moving towards centroid O with equal speed 2m/sec. After collision at O, A stops and C retraces its path with same speed. Distance between B and C just after one second of the collision is αm. Here α is an integer. Find α.
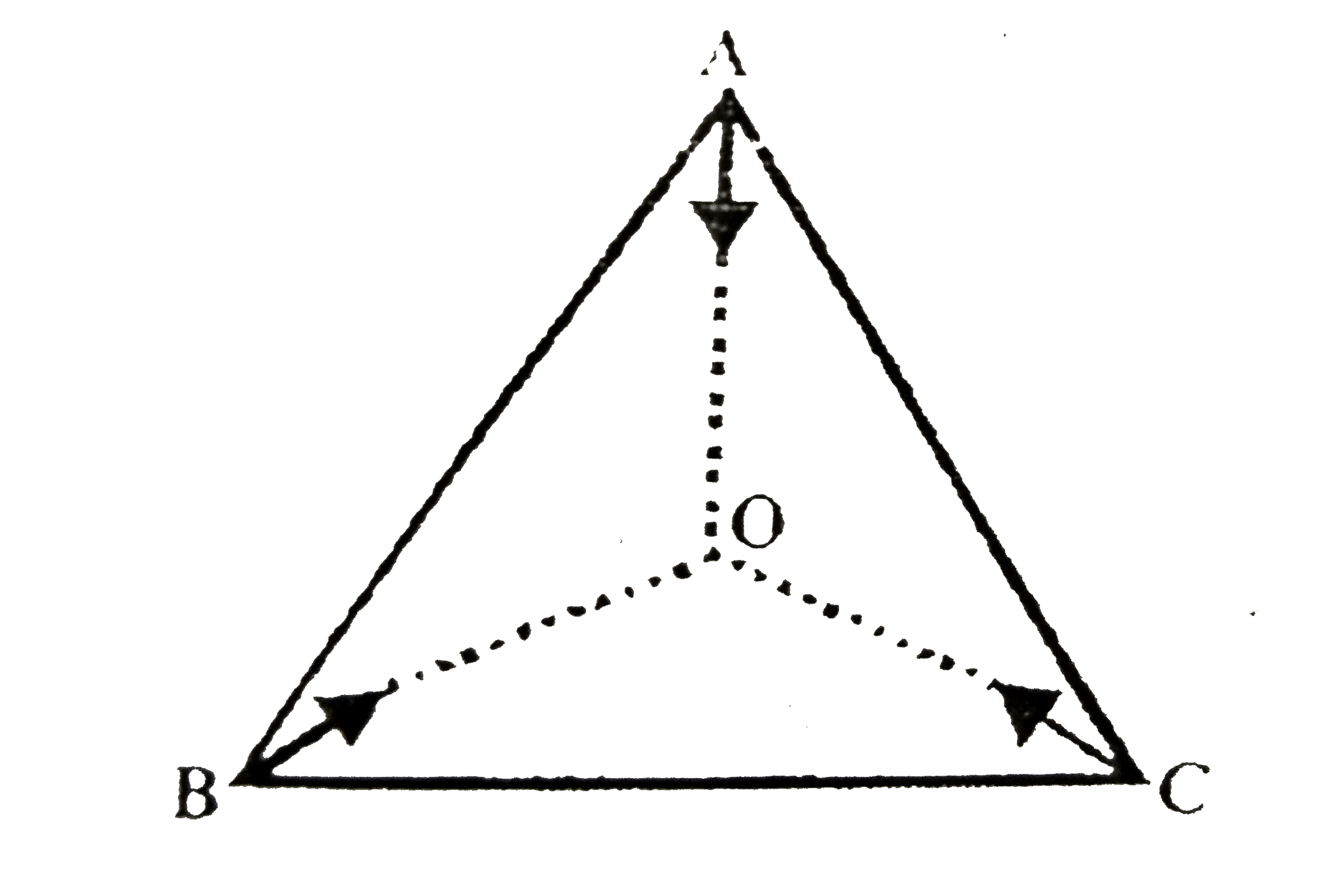
View Solution
Knowledge Check
Three particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
Av along BGBv2alongGBCZeroDv along CGThree particles with equal mass move with equal speed v along the medians of an equilateral triangle as shown. They all collide at the centroid simultaneously. After the collision. A comes to rest, B retraces it's path with same speed. What is speed of C after the collision?
AvBv/2C2vDinformation ijnsufficientThree particles A, B and C of equal masses, moving with the same speed 'v' along the medians of an equilateral triangle, collide at the centroid G of the triangle. After collision, A comes to rest B retraces its path with a speed 'v'. The speed of C after the collision is
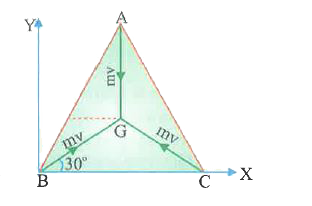AIt iretraces its pathBthe direction in which A cam fromCdoes no haveDopposite to B
Three particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
View SolutionThree particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
View SolutionThree particles each of mass m are located at the vertices of an equilateral triangle ABC. They start moving with equal speeds each along the medians of the triangle and collide at its centroid G. If after collision, A comes to rest and B retraces its path along GB, then C (A) also comes
View SolutionThree particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
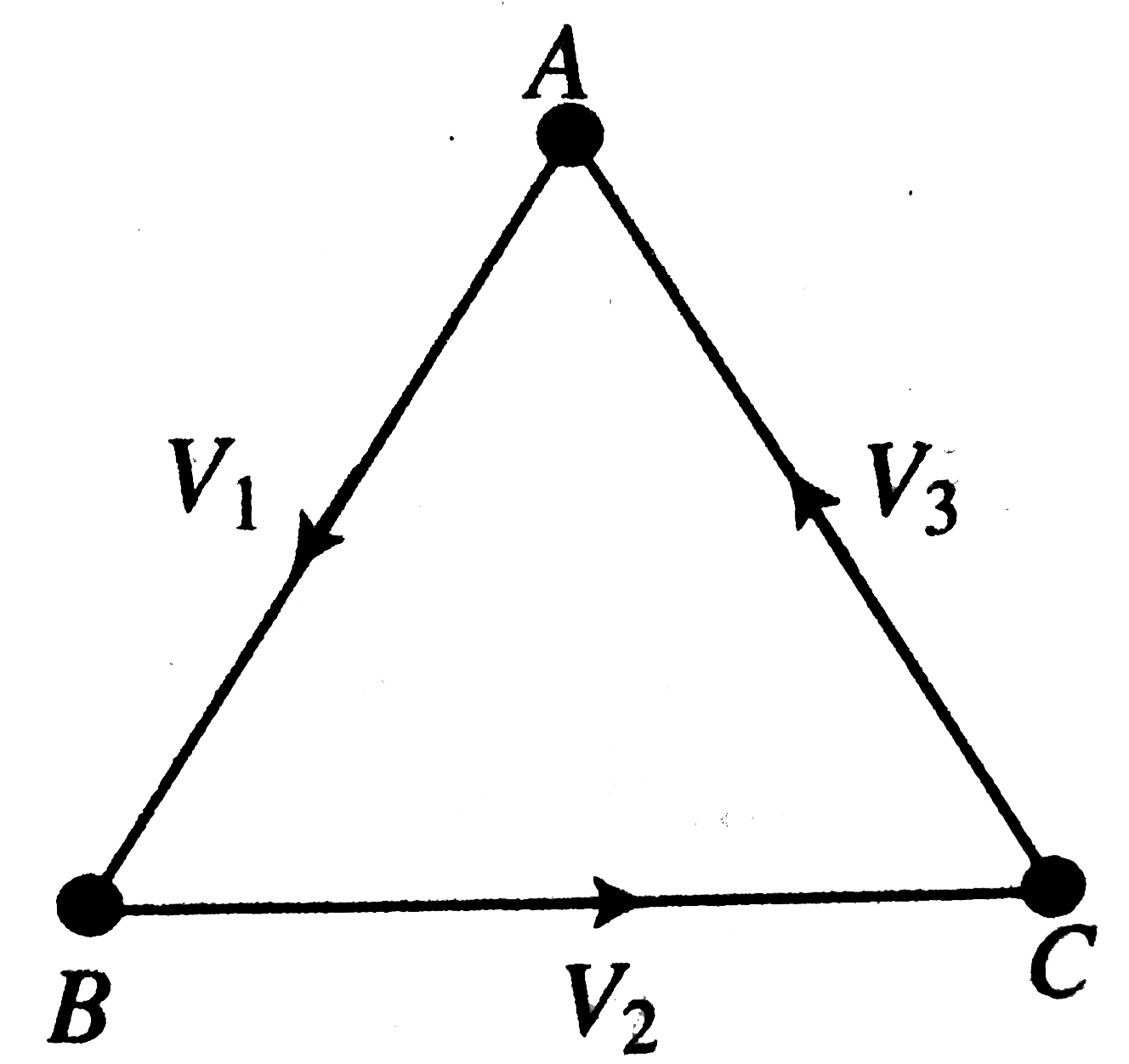
View SolutionThree particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle A starts with a velocity v1 towards line AB, particle B starts with a velocity v2 towards line BC and particle C starts with velocity v3 towards line CA. The displacement of CM of three particle A,B and C after time t will be (given if v1=v2=v3)
View Solution