A bag of mass M hangs by a long massless rope. A bullet of mass in, moving horizontally with velocity u, is caught in the bag. Then for the combined (bag + bullet) system, just after collision
Momentum is mMv/(M+m)
kinetic energy is (1/2)Mv2
Momentum is mv
kinetic energy is m2v2/2(M+m)
The correct Answer is:C, D
COLM:mu+0=(m+M)v⇒v=(mM+m)u
KE after collision
=12(m+M)×(mm+M)2u2=m3u22(m+M)
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-IV A
Explore 32 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
A rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View Solution
Knowledge Check
A bag (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined (bag+bullet) system -
AMomentum is mvMM+mBKinetic energy is mv22CMomentum is mv(M+m)MDKinetic energy is m2v22(M+m)A bag (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined (bag+bullet) system -
AMomentum is (mMv)/(M+m)BKinetic energy is 12Mv2CMomentum ismv(M+m)MDKinetic energy ism2v22(M+m)A beg (mass M) hangs by a long thred and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. The for the combined (bag+bullet) system -
AMomentum is mvM(M+m)BKE is mv22CMomentum is mv(M+m)MDKE is m2v22(M+m)
A wooden log of mass M and length L is hinged by a frictionless nail at O. A bullet of mass m strikes with velocity v and sticks to it. Find the angular velocity of the system, immediately after the collision about O. Also, calculate the minimum value of v so that log becomes horizontal after collision.
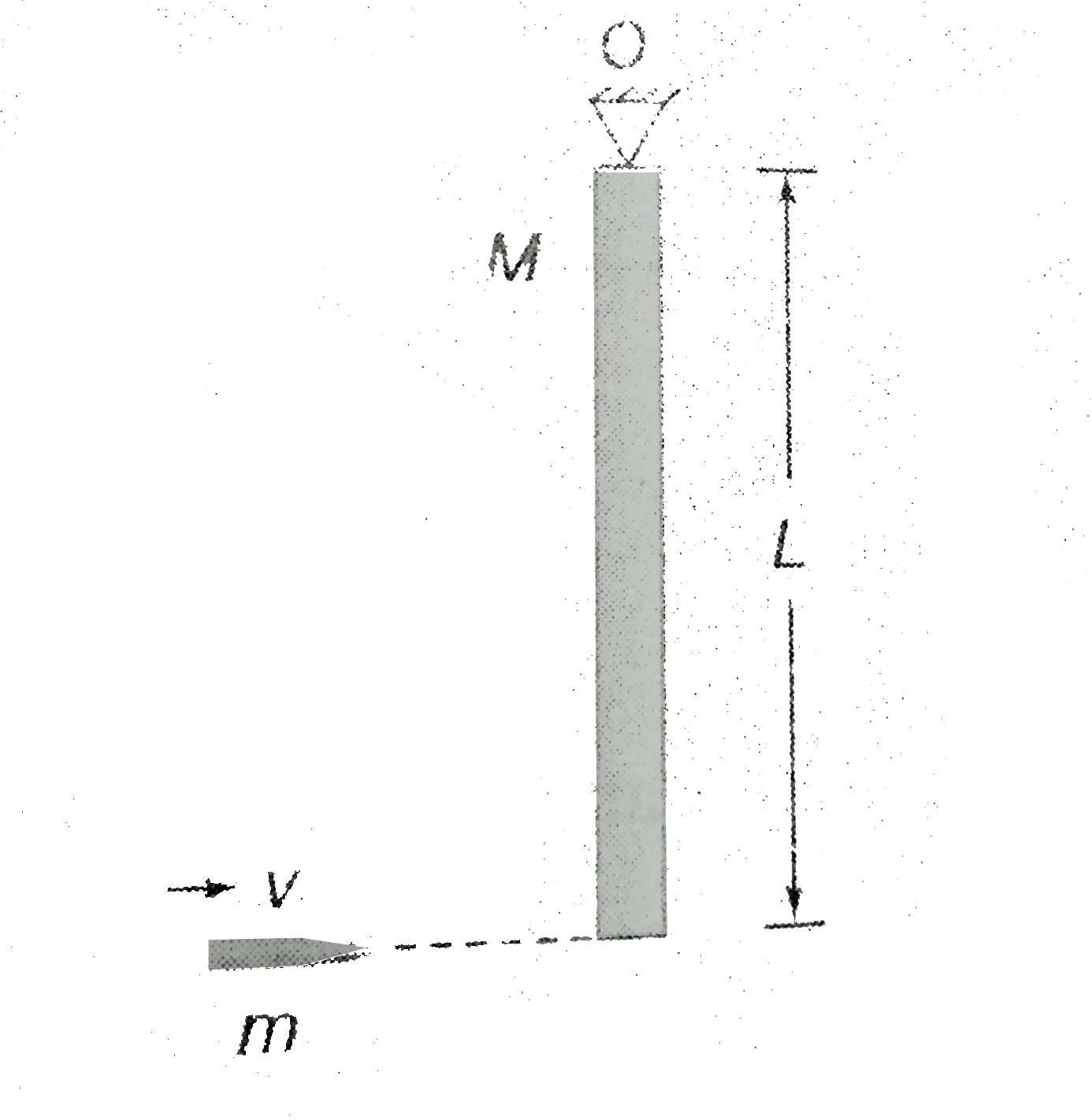
View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
View SolutionA wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is μ , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, travelling with a velocity Vm/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The velocity V of the bullet is

View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?
View Solution

