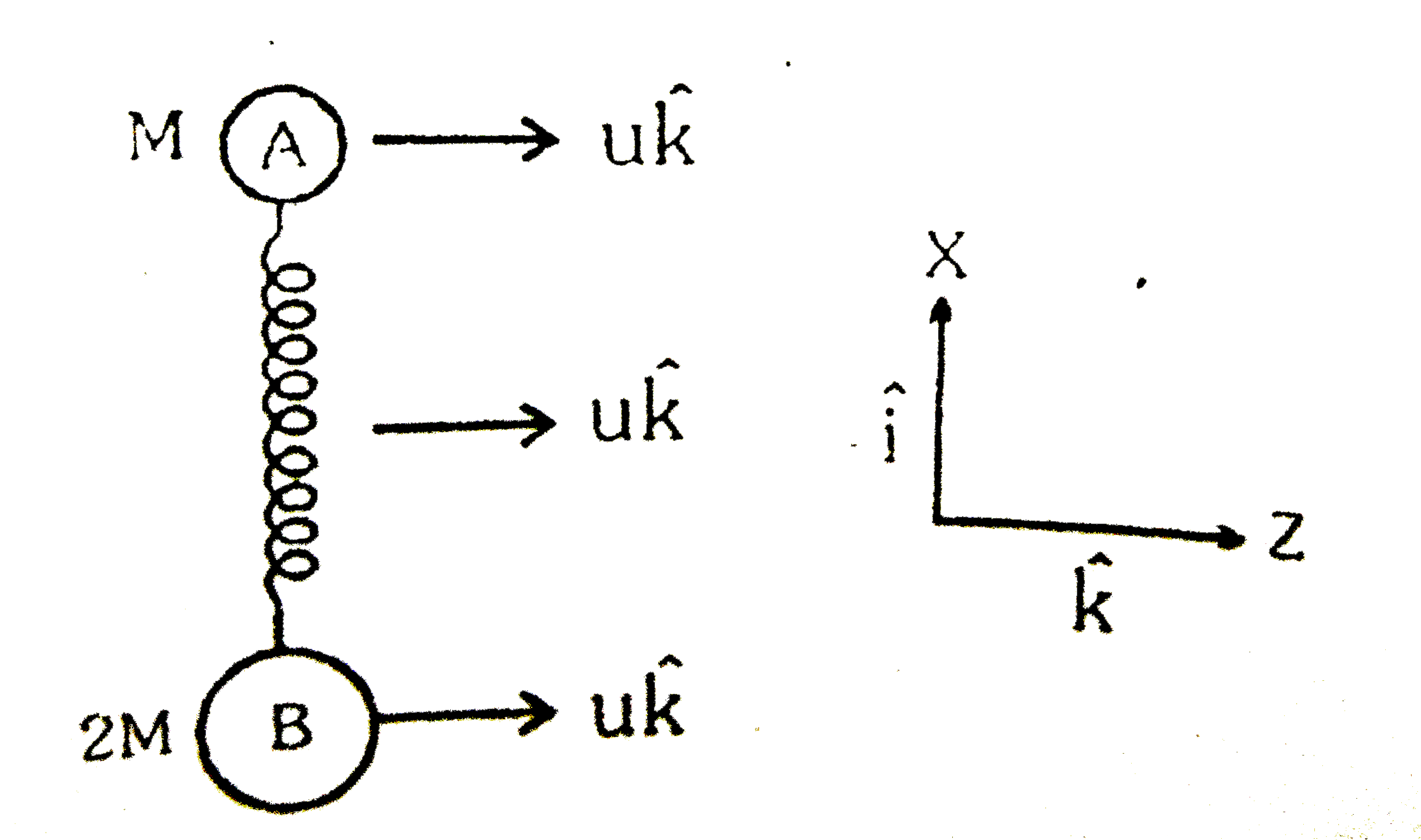
Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
vxˆi+uˆk
−vxˆi+uˆk
−2vxˆi+uˆk
2vxˆi+uˆk
The correct Answer is:C
From COLMMVxA+2MvxB=0⇒vxA=−2vxB
so →vA=−2vxˆi+vˆk
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-IV A
Explore 32 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
Two blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
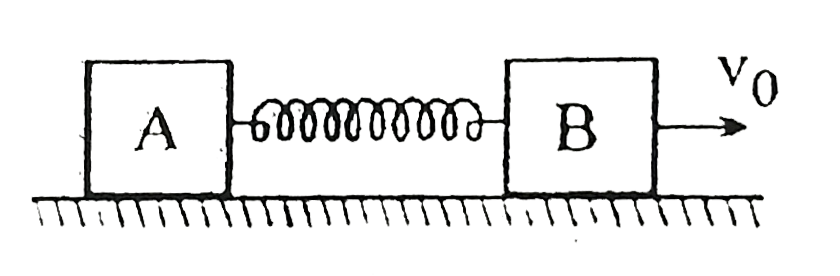 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest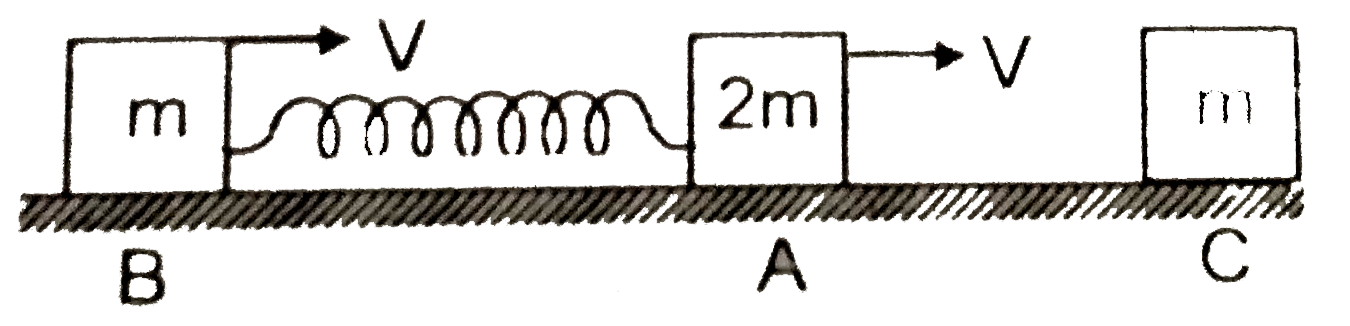
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will beA√32mkVB√27m8KVC√9m8KVD√8m27KVTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in the figure. Mass M is pulled to the right with a force F. If the acceleration of mass m is a, then the acceleration of mass M will be
 A(F−ma)MB(F+ma)MCFMDamM
A(F−ma)MB(F+ma)MCFMDamM
The figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
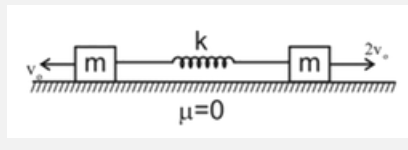
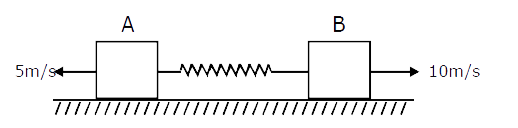
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionTwo blocks of masses m and M are placed on a horizontal frictionless table connected by light spring as shown in figure. The Mass M is pulled to the right with a force F It the acceleration of mass m is a then the acceleration of M will be .

View SolutionTwo blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
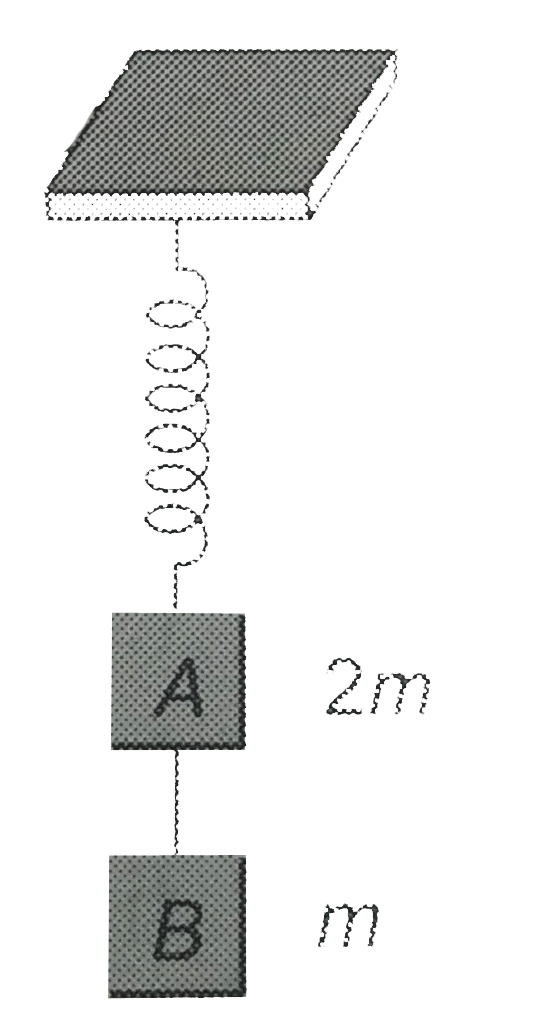
View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively
View Solution

