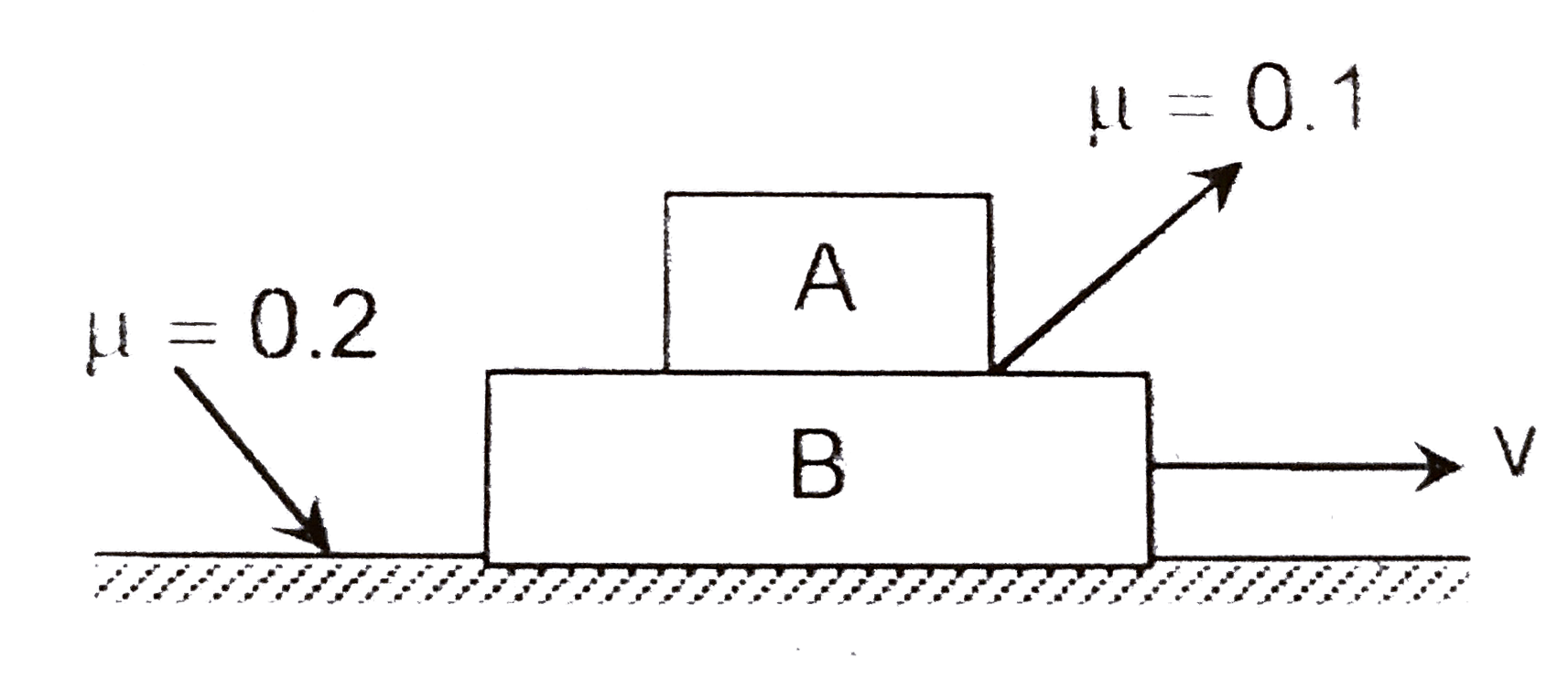
Both the blocks as shown in figure are given together a horizontal velocity towards right. The acceleration of the centre of mass of the system of block is (mA=2mB=2kg).
0m/s2
53m/s2
73m/s2
2m/s2
The correct Answer is:D
acm=FnetTotal mass=(0.2)(3)(10)1+2=2ms−2
Acceleration of 1kg w.r.t. ground
=(0.1)(10)=1ms−2
Acceleration of 2kg w.r.t. ground
=(0.2)(3)(10)−(0.1)(10)2=52ms−2
acm=m1a1+m2a2m1+m2=(1)(1)+(2)(5/2)1+2=2ms−2
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-IV A
Explore 32 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
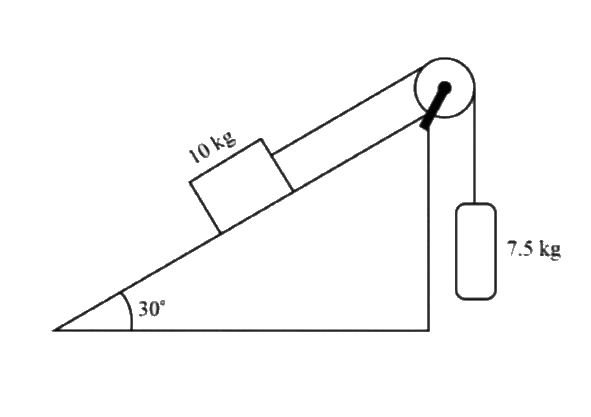
The acceleration of the 10 kg mass block shown in the figure is : -
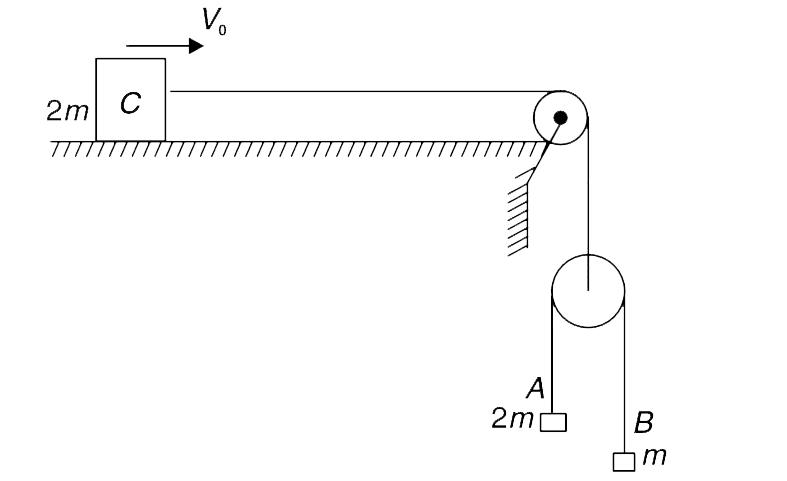
View SolutionIn the shown figure, pulleys and strings are ideal and horizontal surface is smooth. The block C (mass 2m) is given a horizontal velocity of V0=3m/s towards right and the entire system is let go. Find the velocity of three blocks, just after the strings regain tension. Mass of A and B are 2mandm respectively and take g=10m/s2.
View Solution
Knowledge Check

Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2Two block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2In the system shown in the figure, the acceleration of 1 kg block is
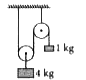 Ag2 downwardsBg2 upwardsCg4 downwardsDg4 upwards
Ag2 downwardsBg2 upwardsCg4 downwardsDg4 upwards
Blocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
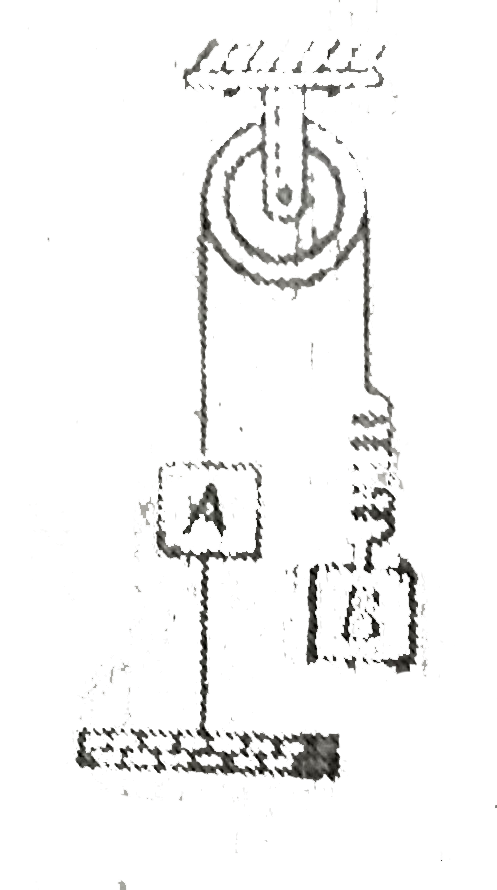
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
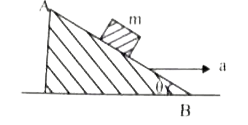
View SolutionA block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

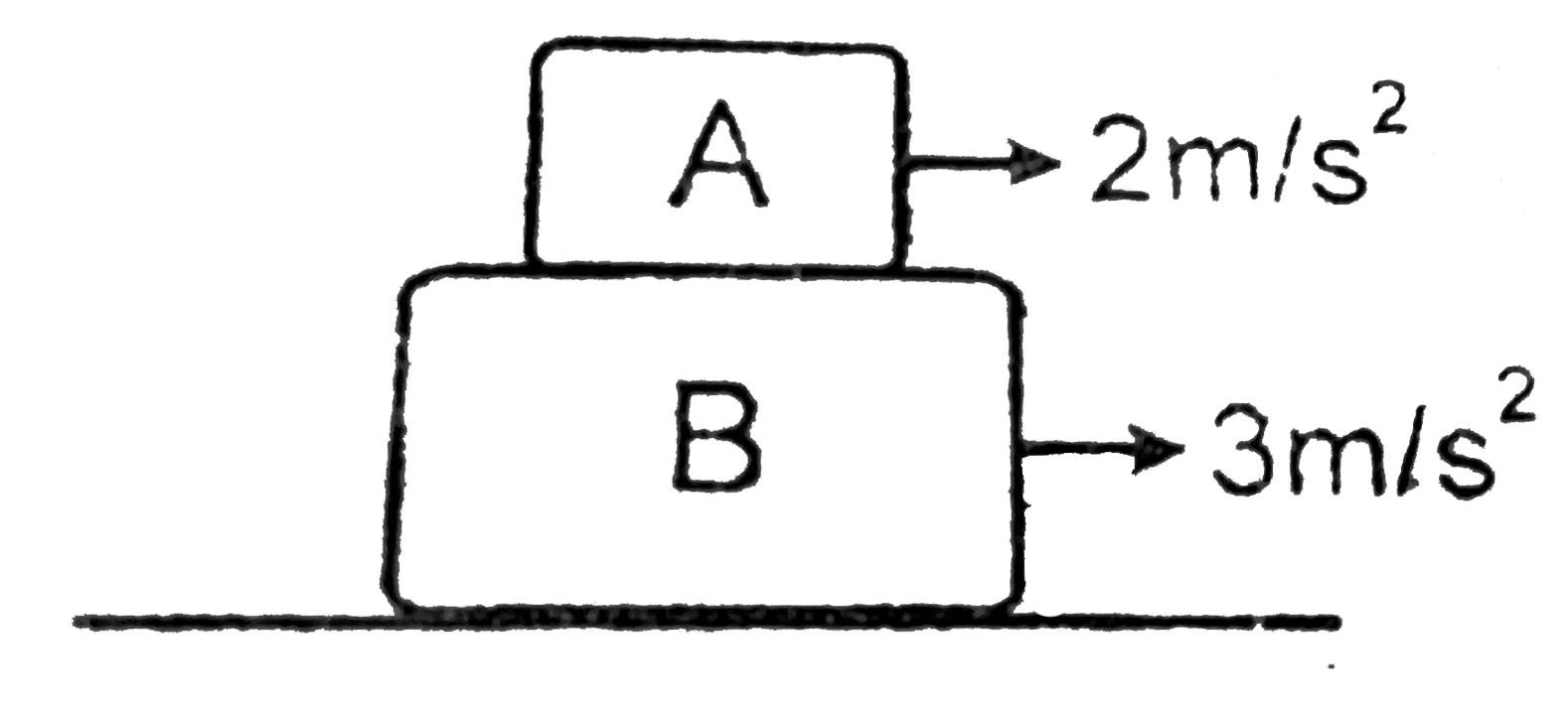
View SolutionBlock A is kept on block B as shown in figure. It is known that acceleration of block A is 2m/s2 towards right and acceleration of block B is 3m/s2 towards right under the effect of unknown forces. Direction of friction force acting on A by B (μAB=0.3)
View Solution

