Infinite numbers of bloks are placed on a table on a edge as shown in the diagram.
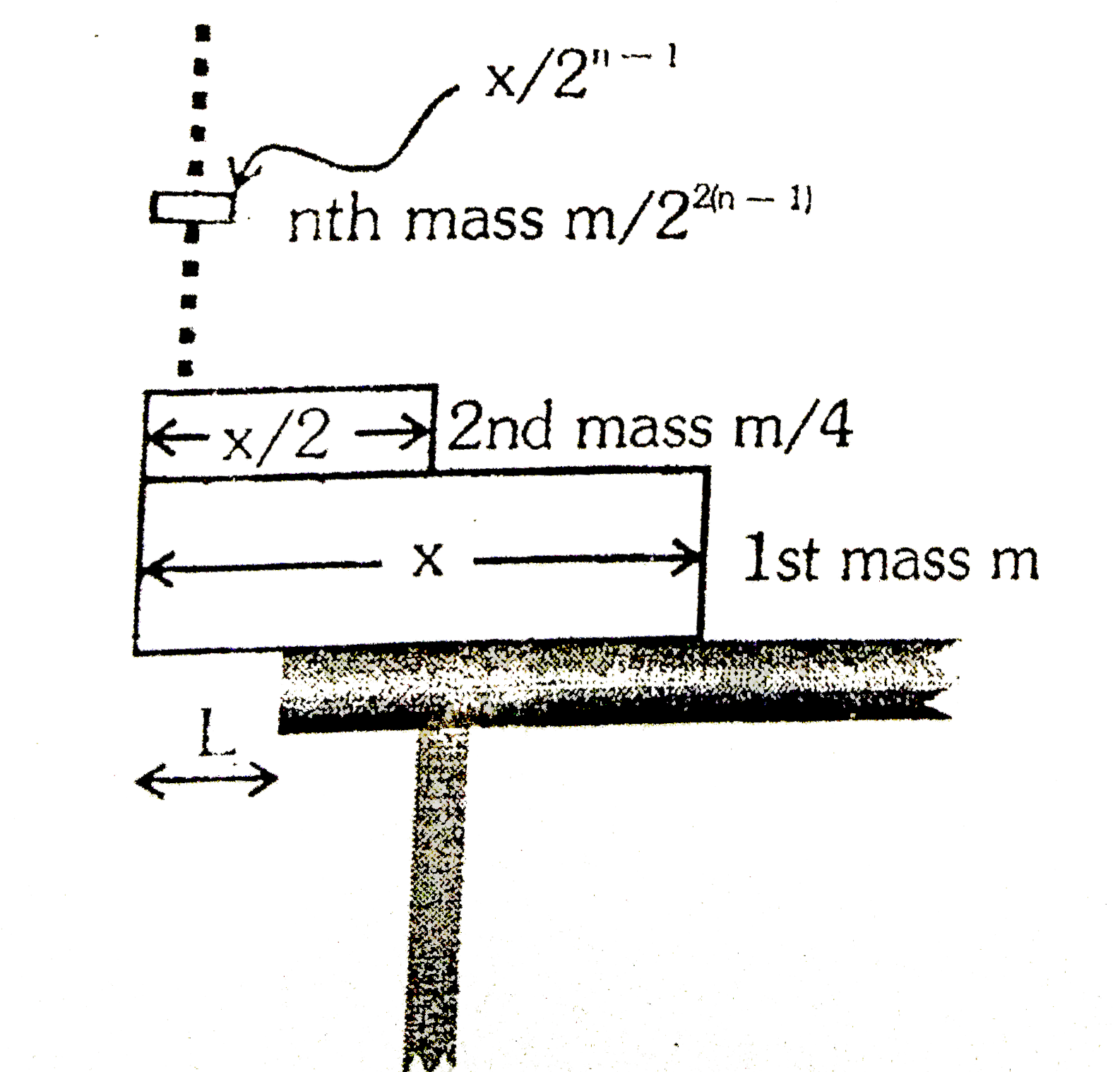
What is the minimum value of L so that the blocks are just going to topple over the table ?
x/3
2x/5
3x/7
4x/9
The correct Answer is:C
Centre of mass of combination should lie on edge of table.

xCOM=0
xCOM=[m(x2−L)+m4(x4−L)+m16(x8−L)]∑M=0
x2[1+18+182+.......]−L[1+14+142+......]=0
x2⎡⎣11−18⎤⎦−L⎡⎣11−14⎤⎦=0
L=3x7
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A cuboid of height 10 cm, width 5 cm and 8 kg is kept on a rough horizontal ground as shown . The ground is so rough that we can assume that the questions indicated below. A boy applies a horizontal force F at the top edge of the cuboid.

What is the minimum value of F so taht the block begins to topple ?
View SolutionA block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

View Solution
Knowledge Check
A uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)
 AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1
AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1What is the minimum value of the mass M so that the block is lifted off the table at the instant shown in the diagram ? Assume that the blocks are initially at rest.
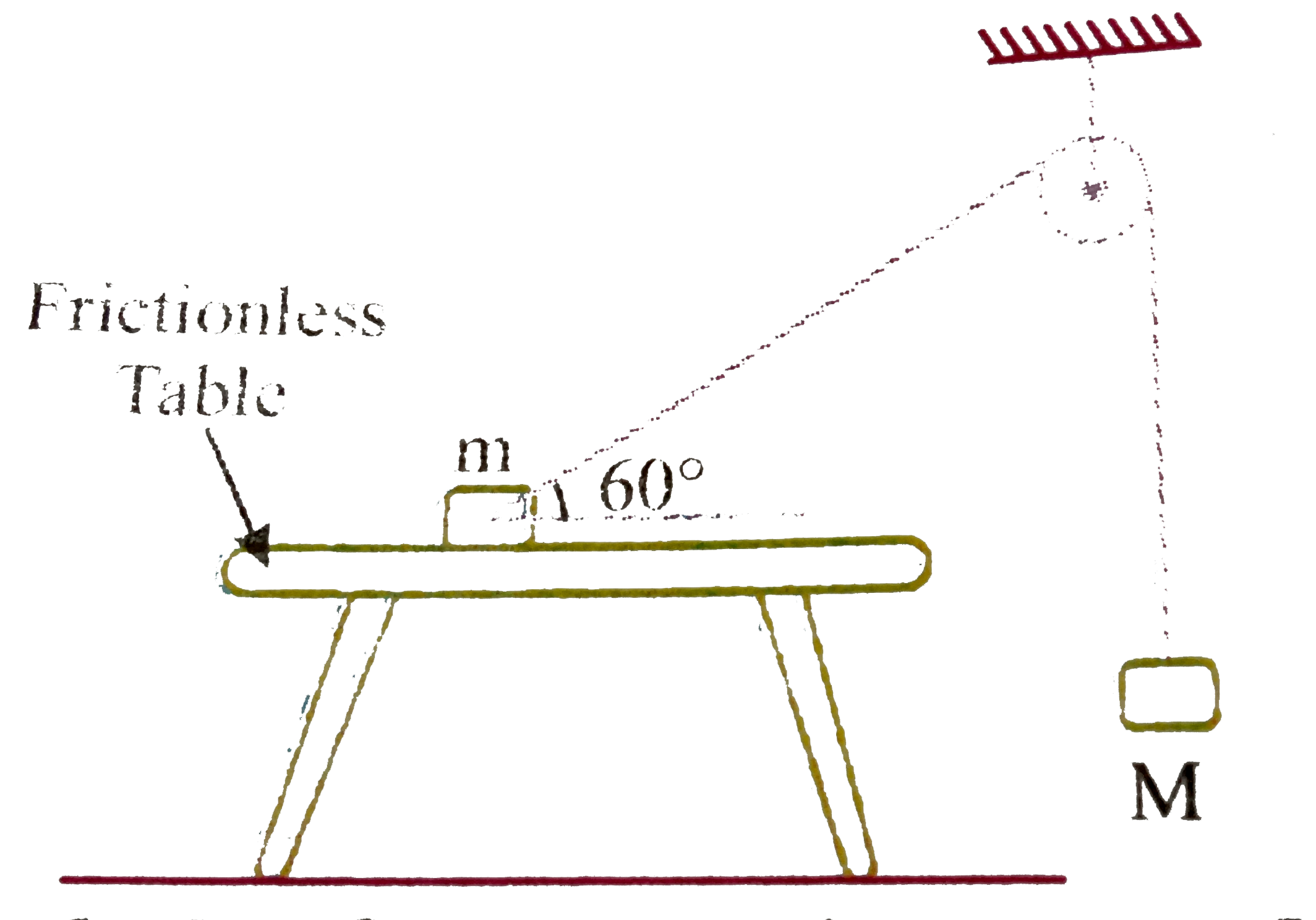 .Amsin60∘Bmtan60∘Cmsin60∘Dnone of these
.Amsin60∘Bmtan60∘Cmsin60∘Dnone of theseThe coefficient of static friction μs between block A of mass 2kg and the table as shown in is 0.1 What would be the maximum mass value of blocks B so that the two bloks do not move ? The string and the pulley are assumed to be smooth and massless (g=10m/s2)
 .A0.2kgB0.4kgC2.0kgD4.0kg
.A0.2kgB0.4kgC2.0kgD4.0kg
A block is rotating in contact with vertical wall (rotor) as shown. Find the minimum value of ω so that the block does not slide down.

View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
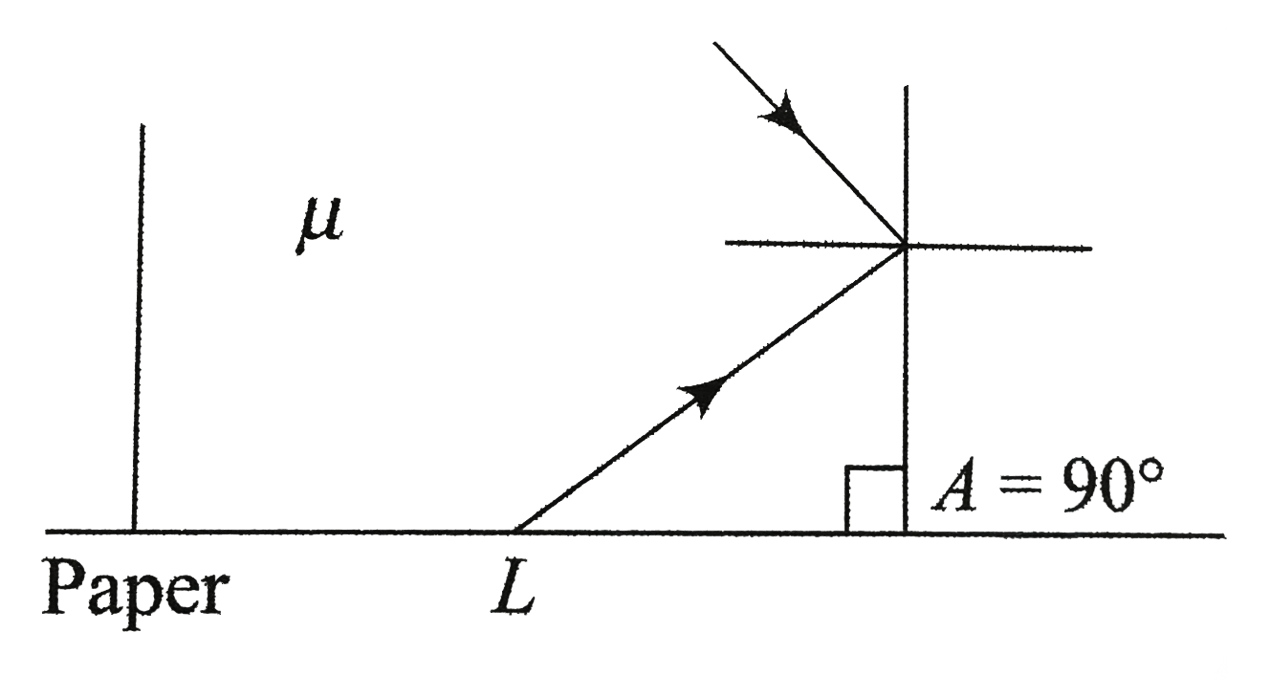
View SolutionThree blocked A,B and C are placed one over the other as shown in figure. Draw free body diagram of all the three blocks.

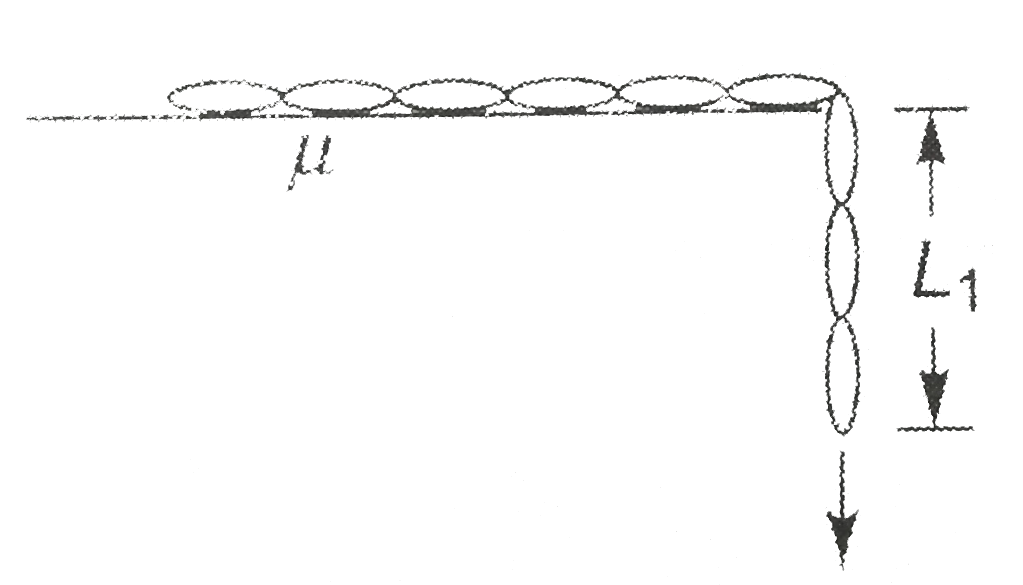
View SolutionA homogeneous chain of length L lie on a table. If the coefficent of friction is μ , find the maximum length L1 of the chain which can hang from the edge of the table without the chain sliding down.
(b) Consider the situation as shown in the figure. Find teh minimum value of m so that the blocks do not move.

View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.
View Solution