For infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :

34
45
2
12
The correct Answer is:A
Let the equivalent resistance of one infinite ladder be x. Then the complete network reduces to
∴RAB=x×3xx+3x=34x
and RAC=(2X×2x)=x

Here RABRAC=34
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
100 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
18 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Idnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
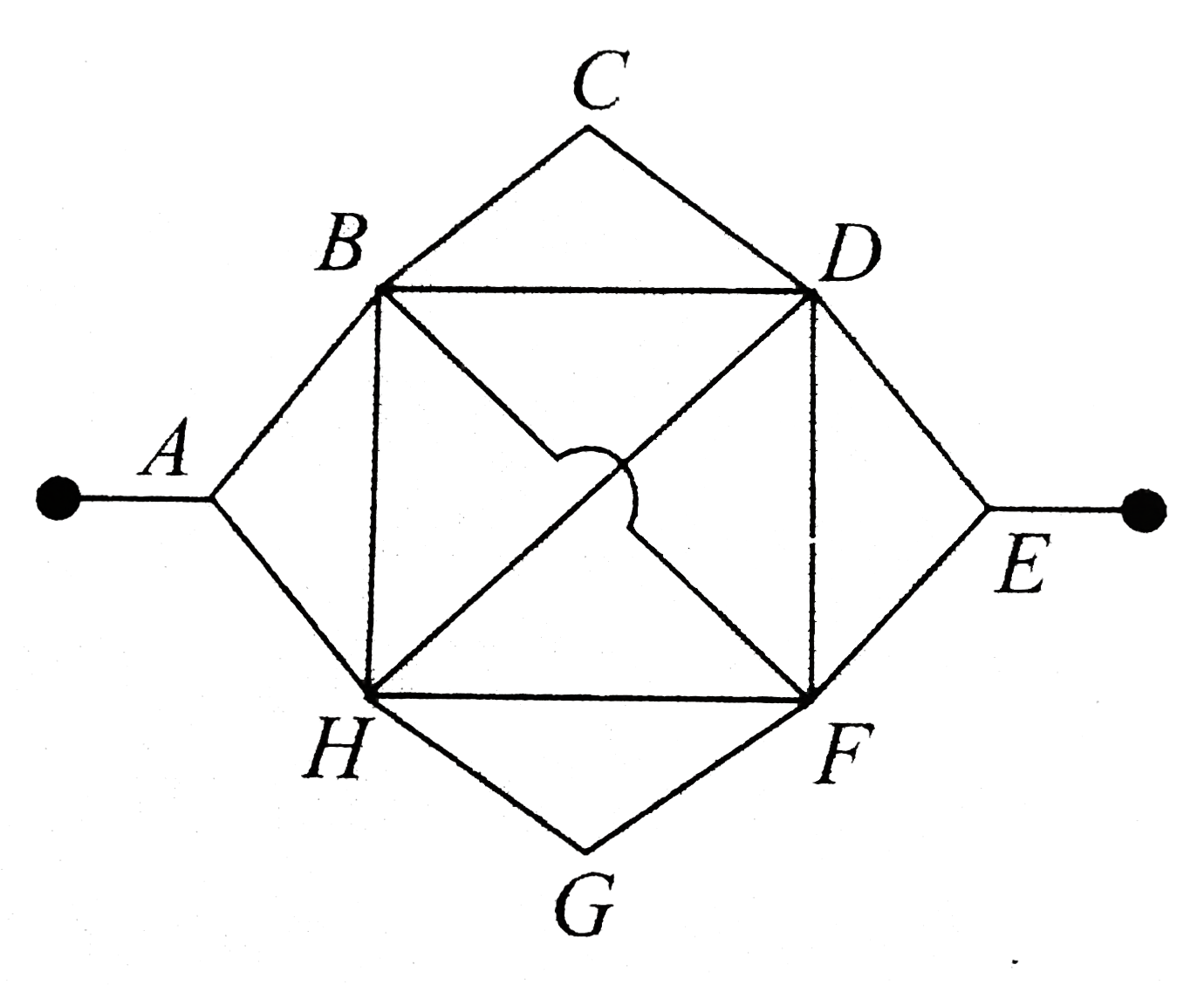
View SolutionFour identical resistances are joined as shown in the figure. The equivalent resistance between points A and B is R1 and that between A anc C is R2 then ratio R1/R2 is
View Solution
Knowledge Check
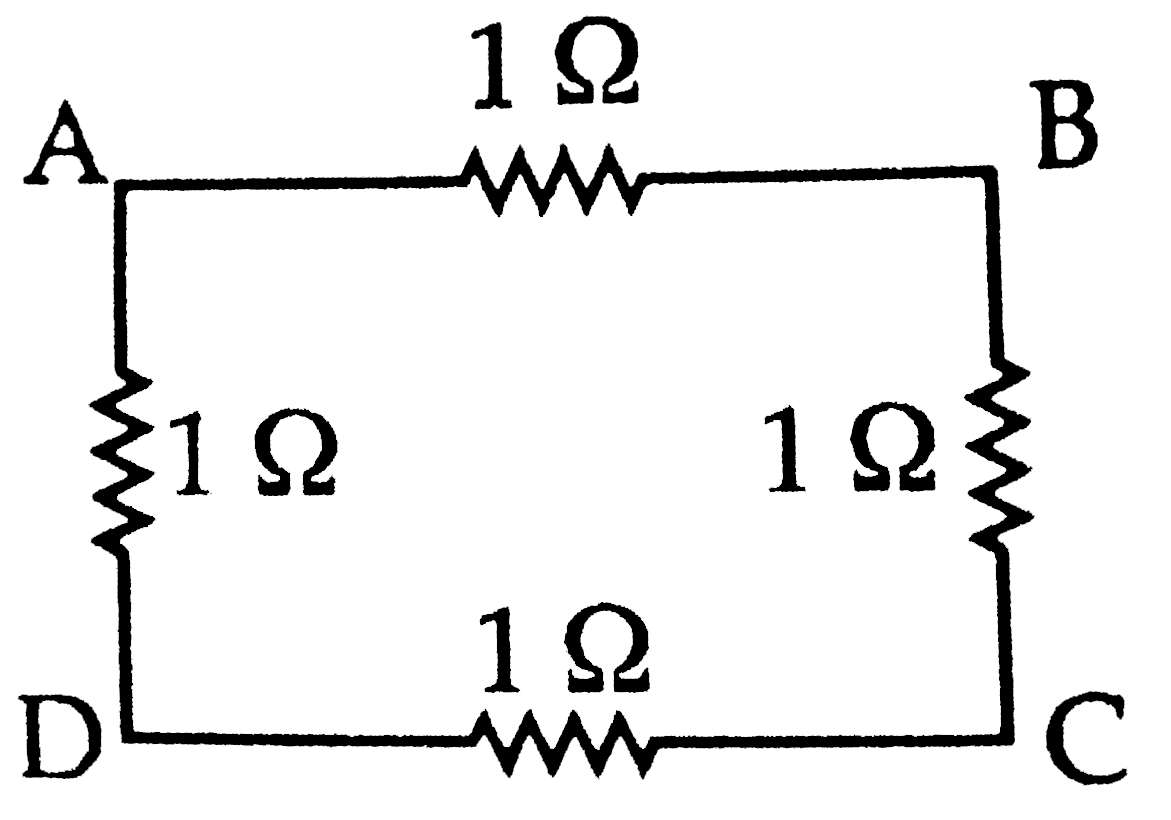
Three equal resistances each of value R are joined as shown in the figure. The equivalent resistance between M and N is
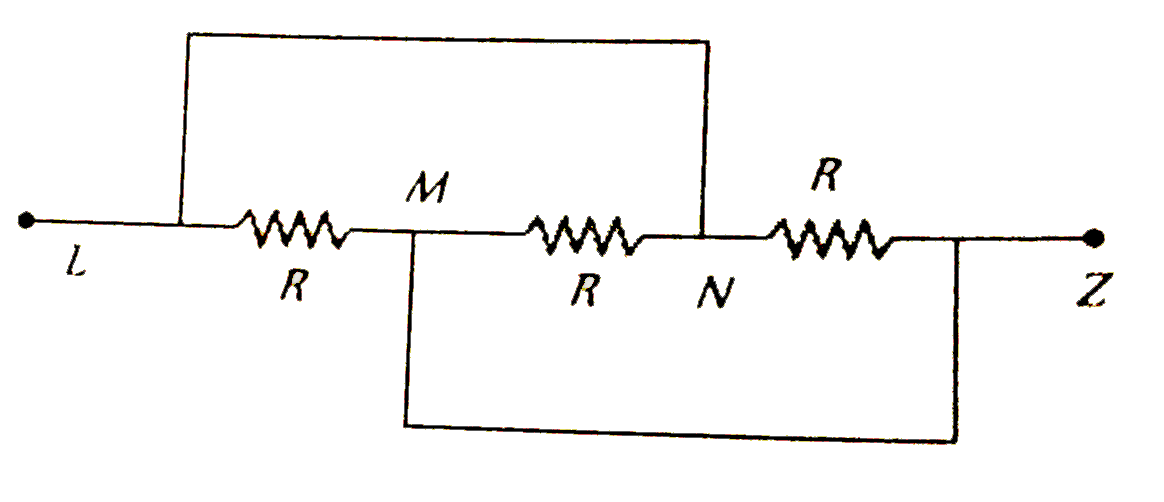 ARB2RCR2DR3
ARB2RCR2DR3Four identical resistance are joined as shown in fig. the equivalent resistance between points A and B is R1 and that between A and C is R2. Then ratio of R1R2 is
 A1:5B3:4C2:5D1:2
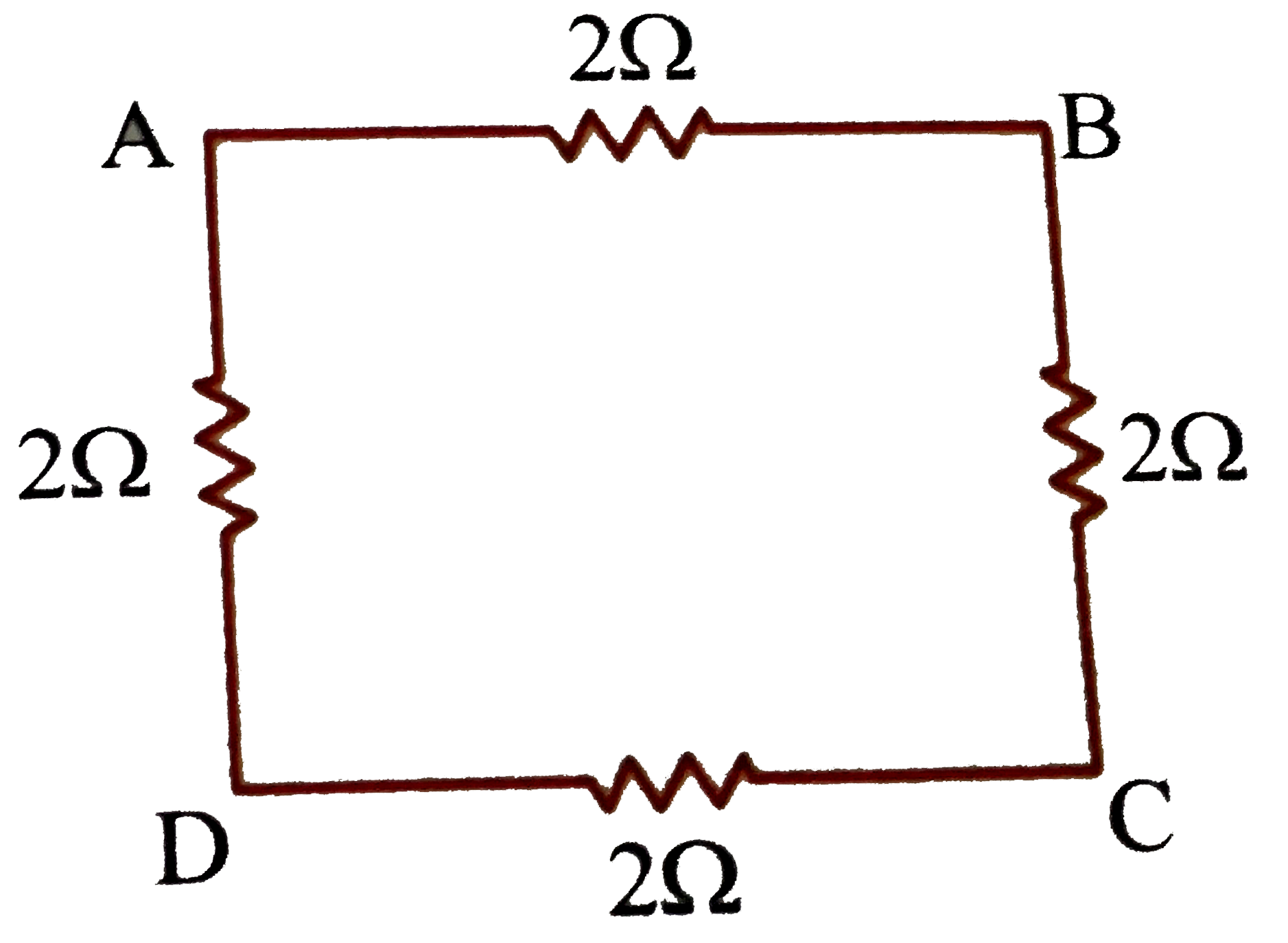
A1:5B3:4C2:5D1:2Four identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 ARB2RC3RD4R
ARB2RC3RD4R
Each resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
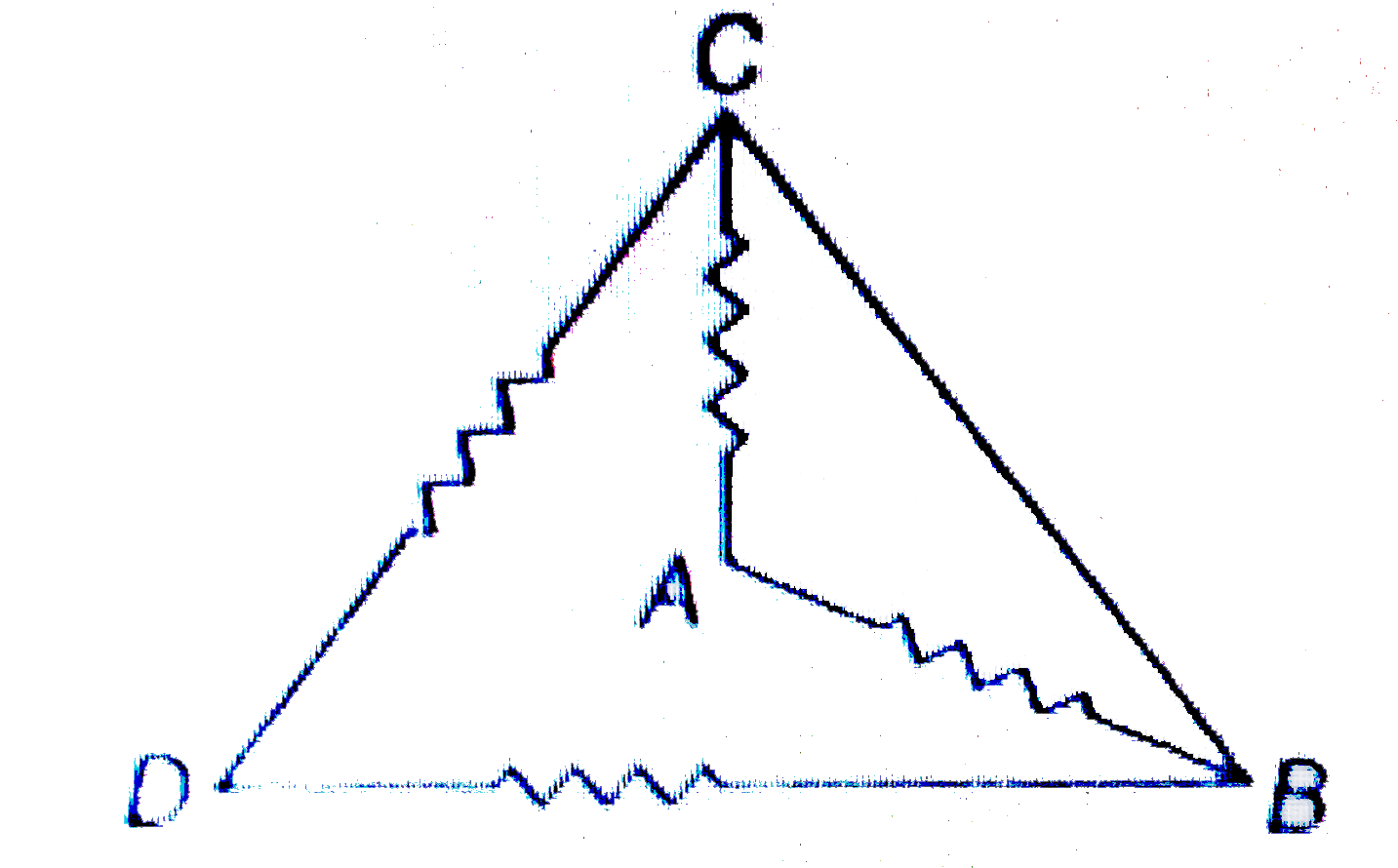
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure.
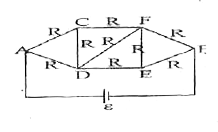
The equivalent resistance between A and B is
View SolutionInside a supeerconducting ring, six identical resistors each of resistance R are connected as shown in figure. The equivalent resistances.
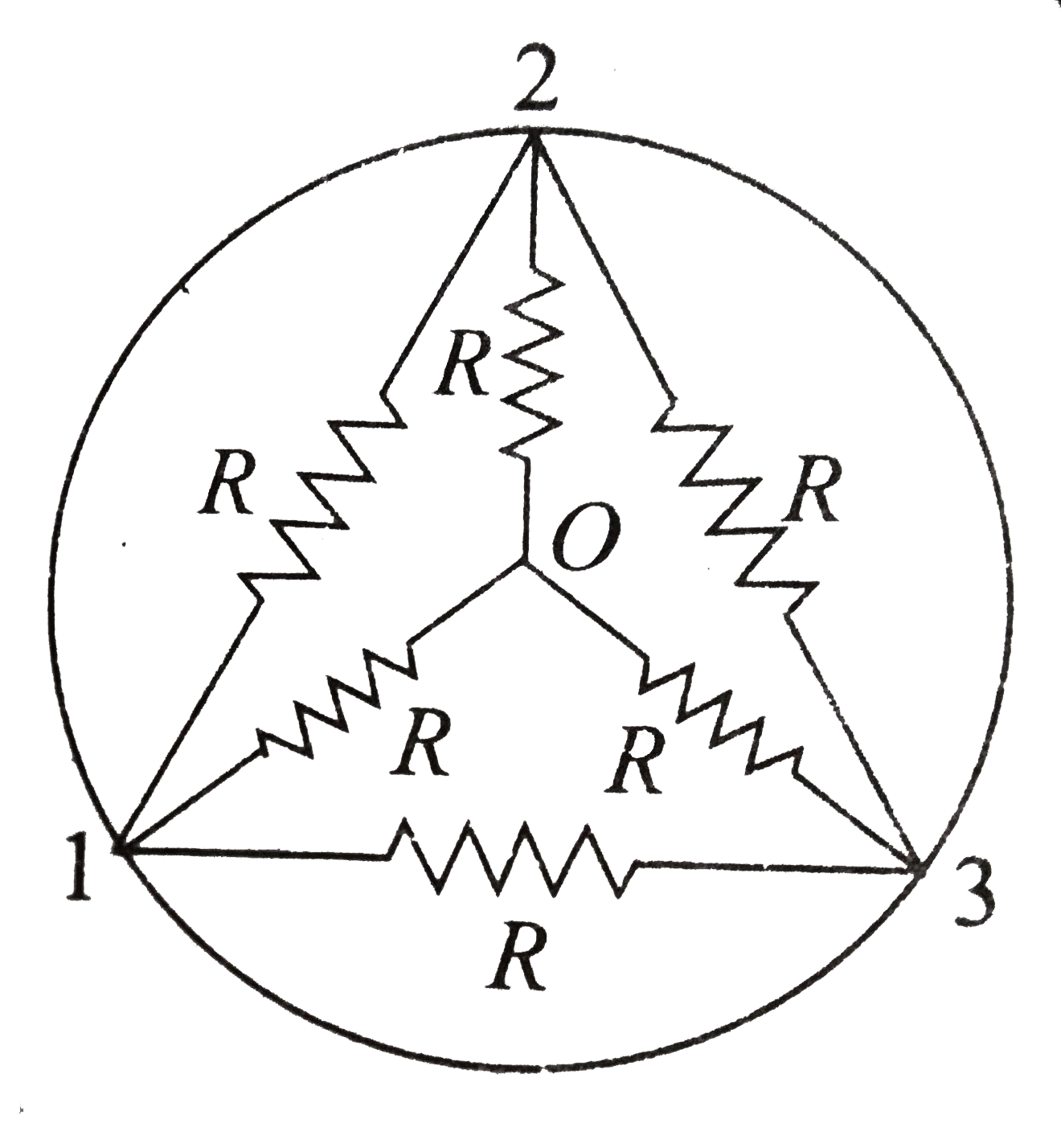
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B is
View SolutionThree equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
View Solution
