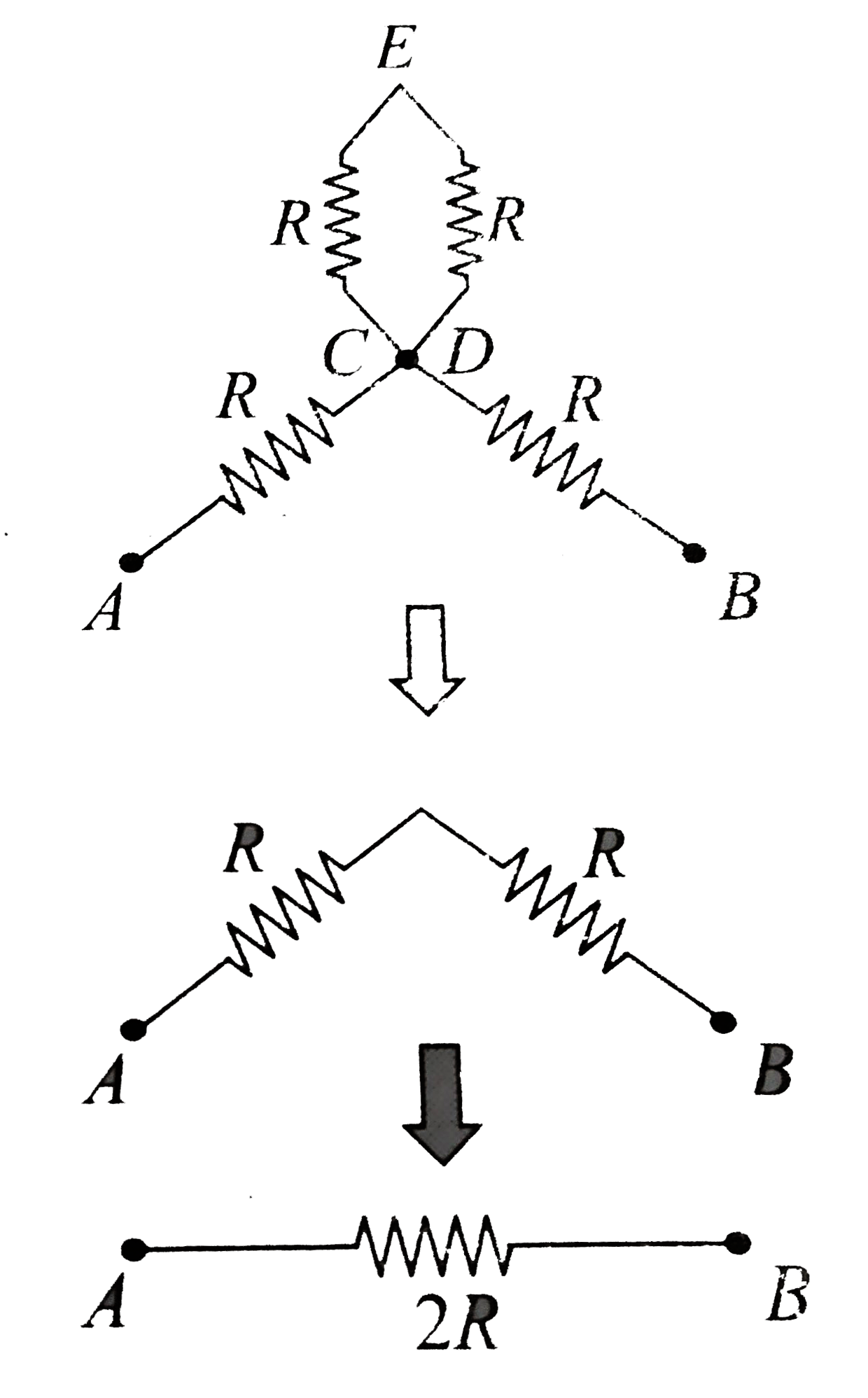
Four identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.

A
R
B
2R
C
3R
D
4R
Video Solution
Text Solution
The correct Answer is:B
Since C and D are conneted with
a zero resistor, they are equipotential.
Then superimpose C and D to obtain
the simplified circuit as shown. Since no
current flows in the branches CE and ED
cut and then thro them to have
RAB=R+R=2R
If we get a closed loop of resistors
without any battery, it carries no current
Then remove the total loop to get a
simpler circuit or if the current in any
branch is zero, remove it.
|
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Solved Examples
Explore 12 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.1
Explore 28 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check
Three equal resistances each of value R are joined as shown in the figure. The equivalent resistance between M and N is
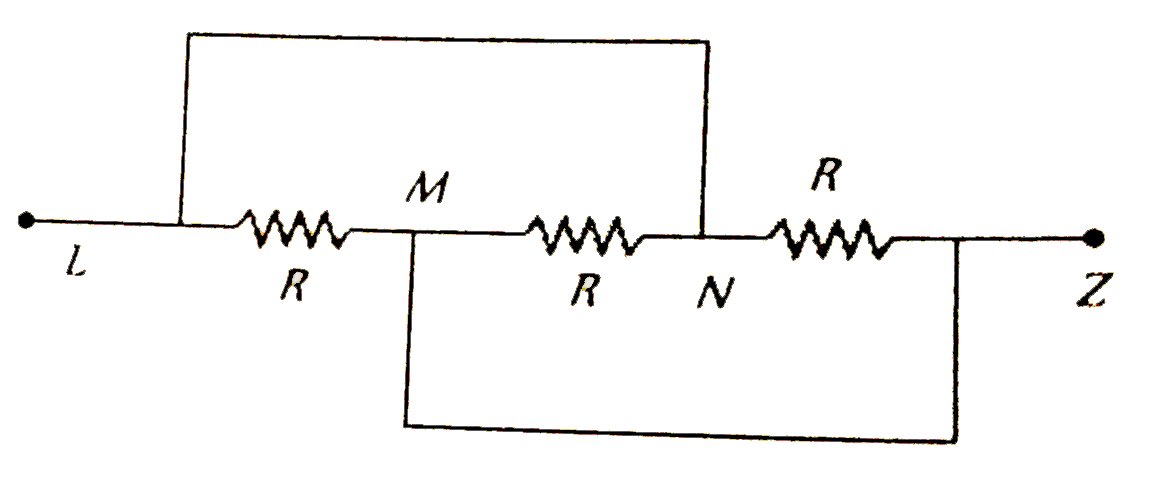 ARB2RCR2DR3
ARB2RCR2DR3Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
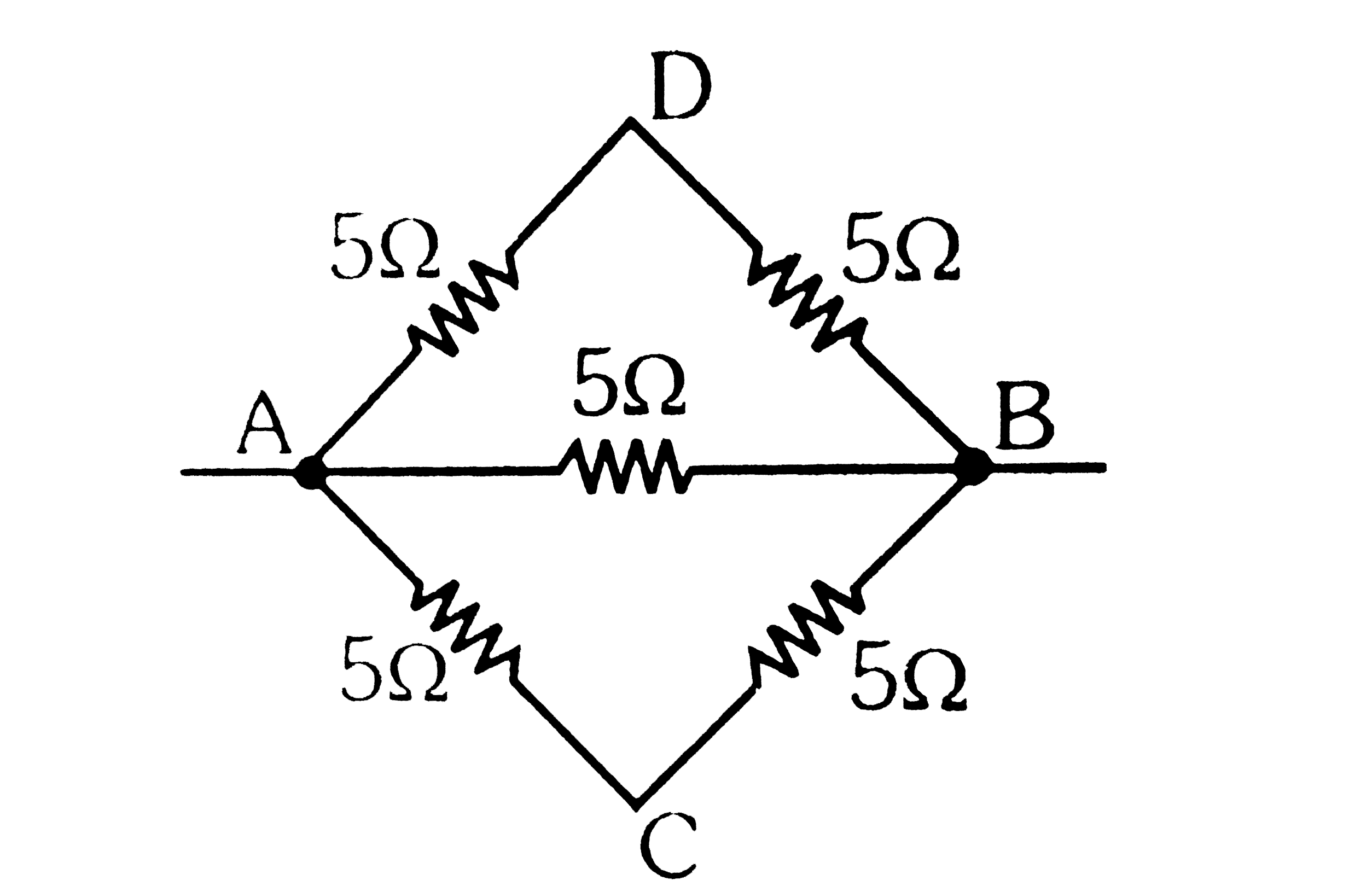 A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5Ω
A(1) 7.5Ω (2) 2.25ΩB(1) 5Ω (2) 2.50ΩC(1) 2.5Ω (2) 3.13ΩD(1) 3Ω (2) 2.5ΩFor infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :
 A34B43C2D12
A34B43C2D12
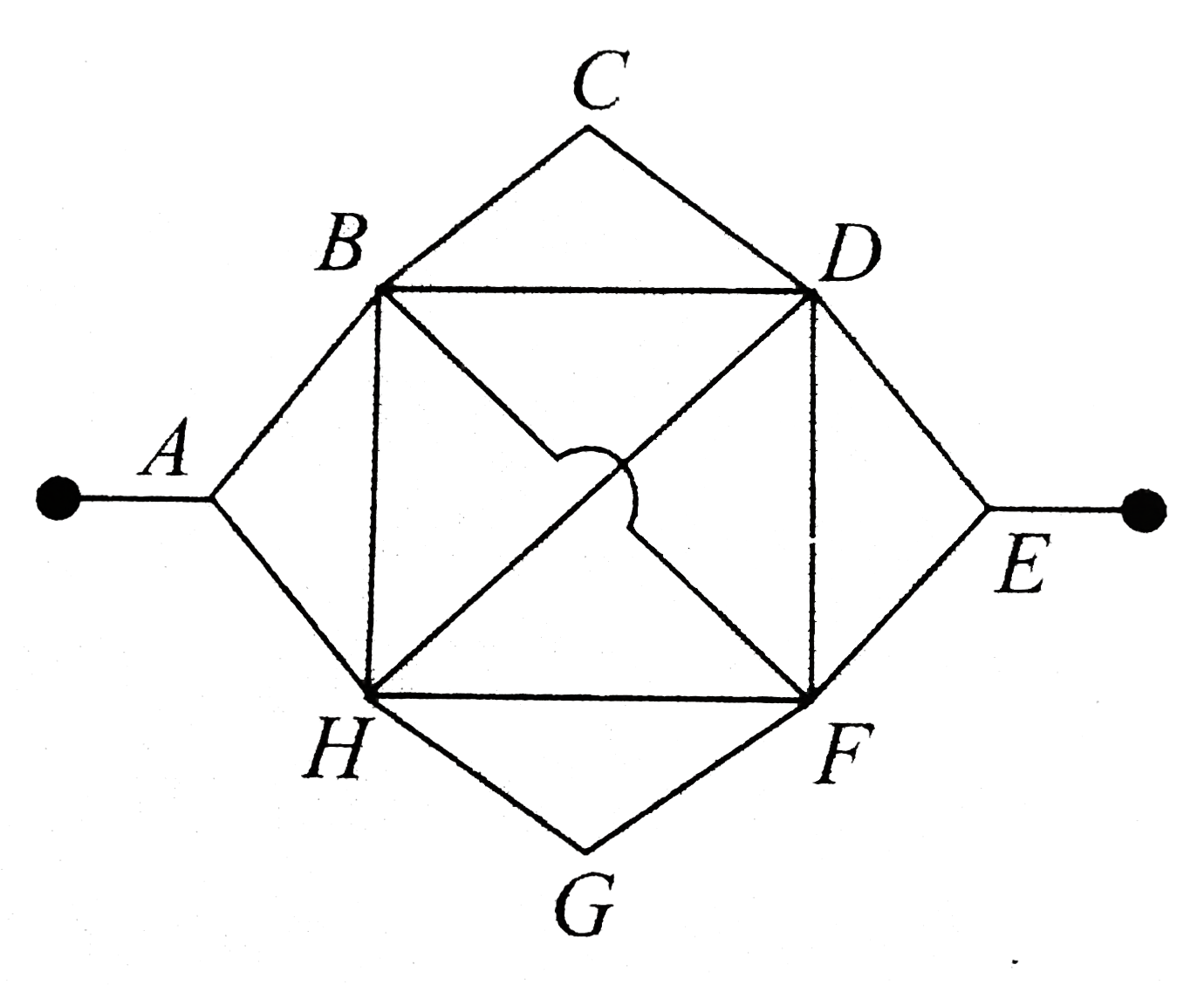
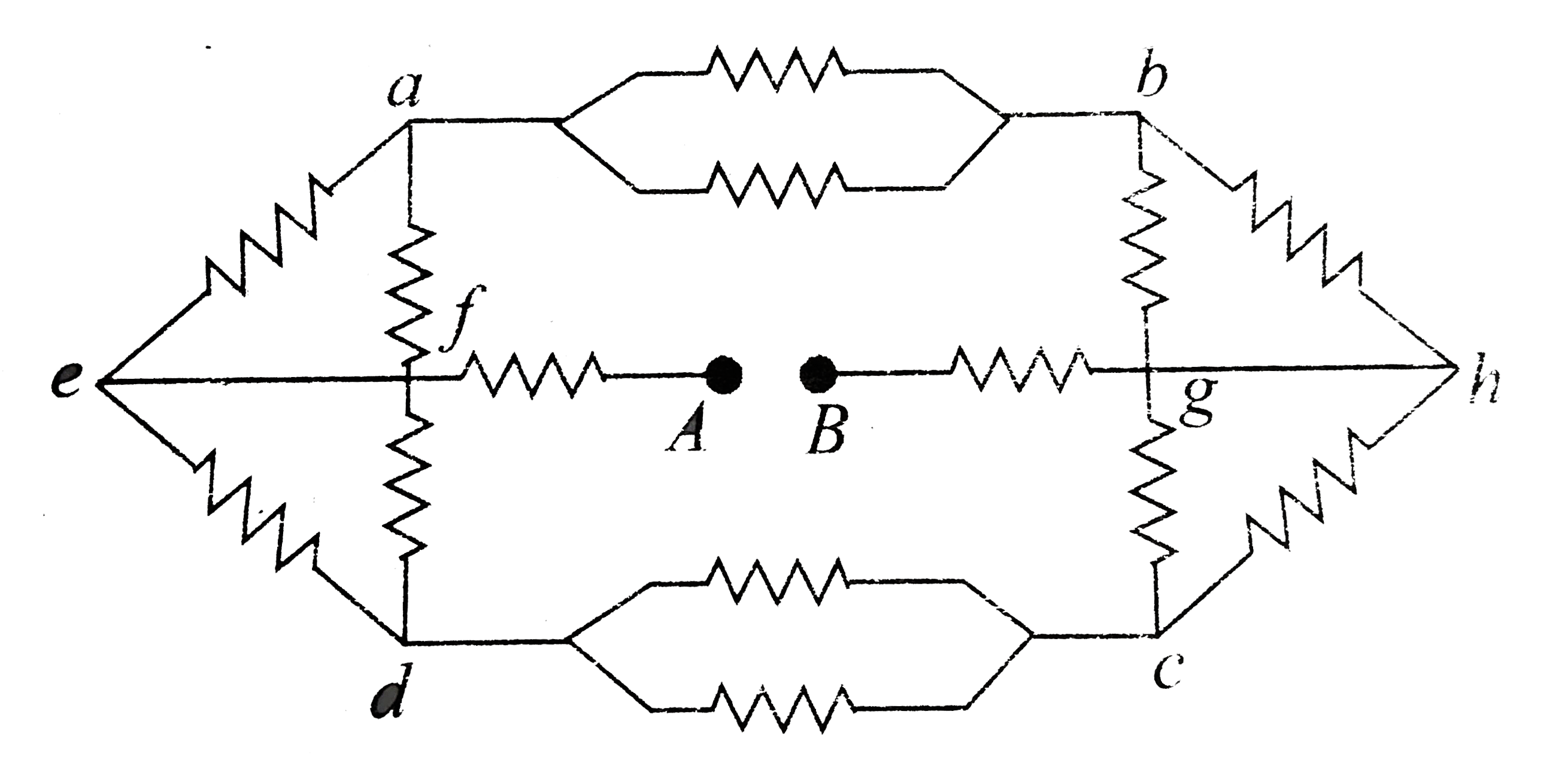
Idnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
View SolutionFour identical resistances are joined as shown in the figure. The equivalent resistance between points A and B is R1 and that between A anc C is R2 then ratio R1/R2 is
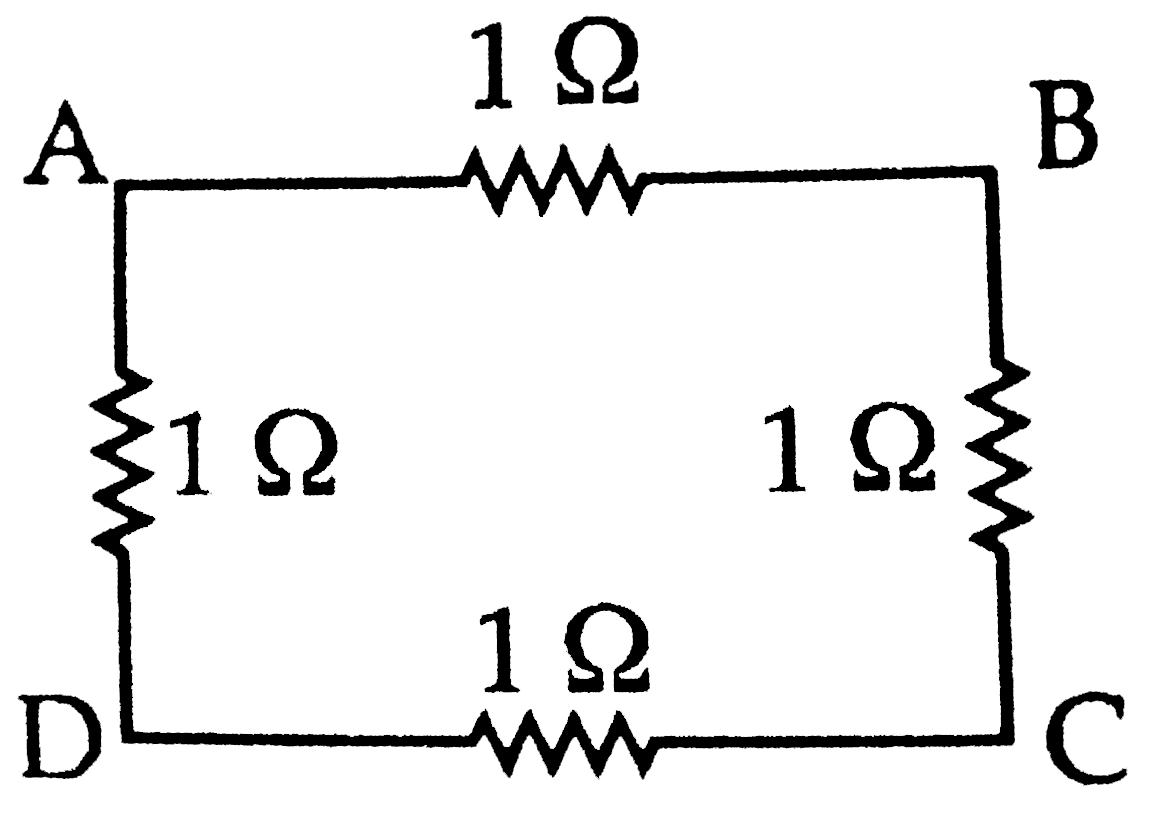
View SolutionEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
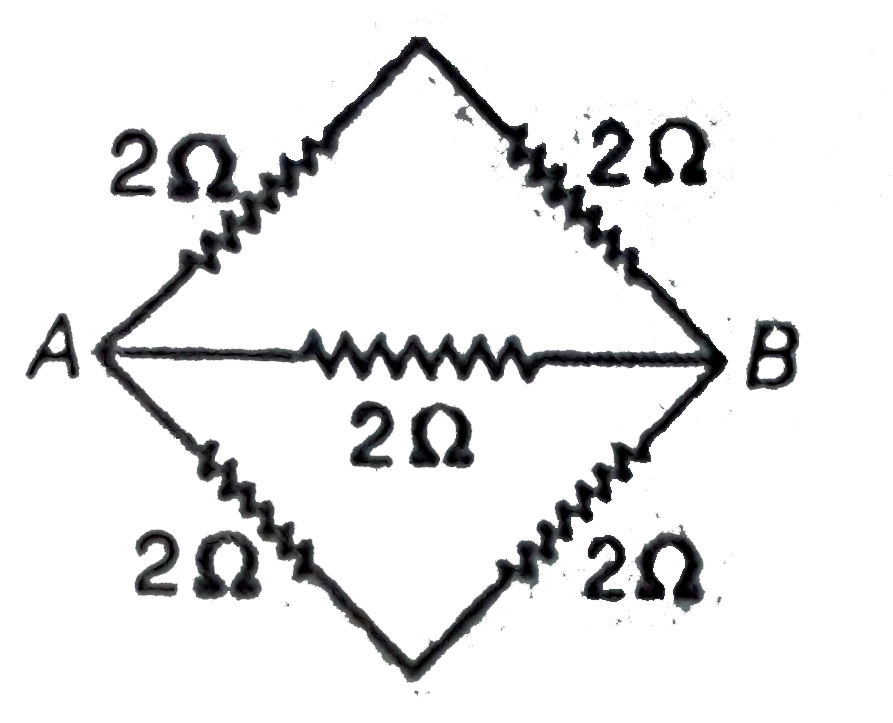
View SolutionEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
View SolutionThree equal resistors, each equals to r are connected as shown in figure. Then, the equivalent resistance between points A and B is
View Solution


 .
.