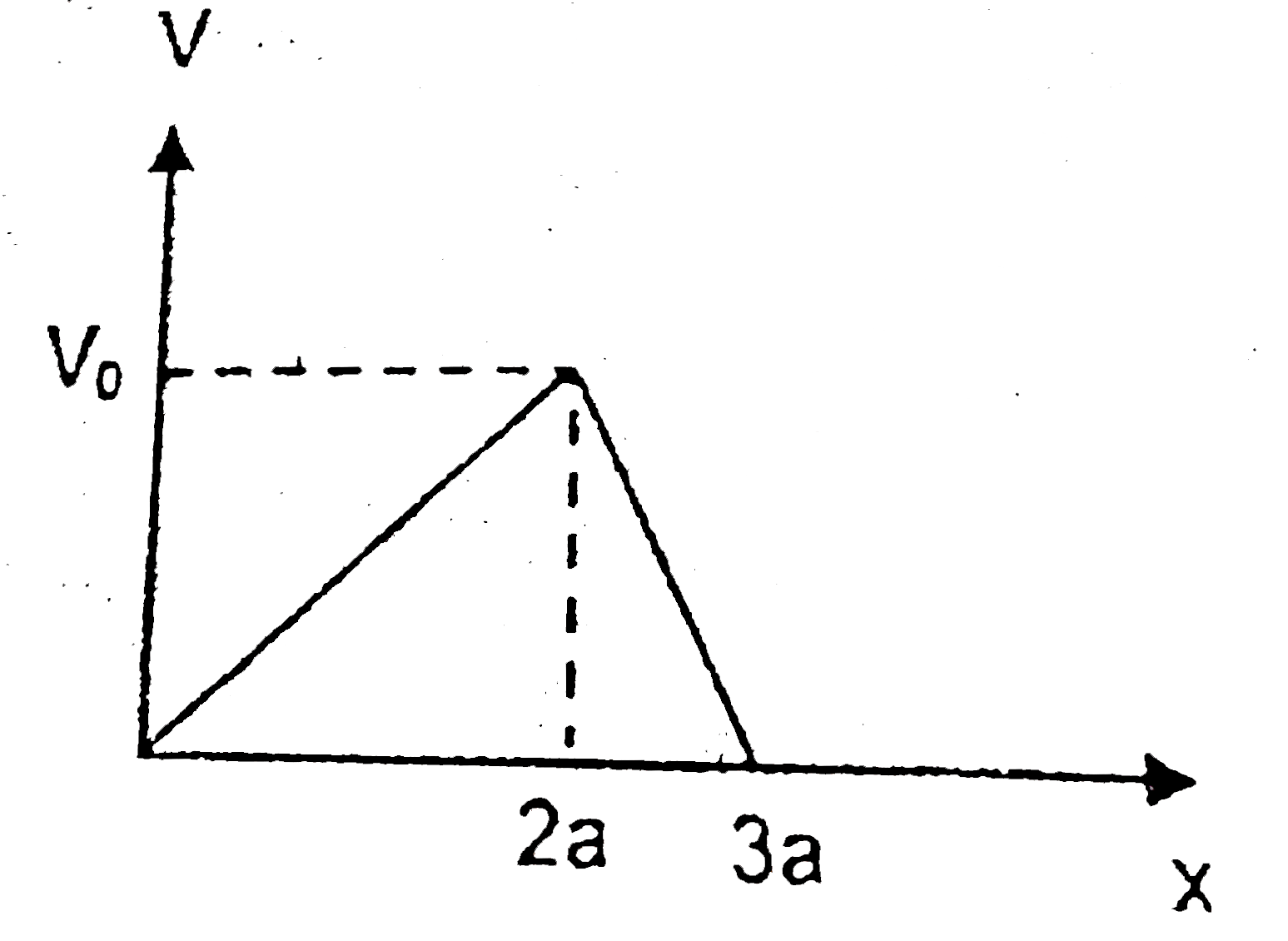
There exist electric field in space such that potential gradient along y-axis and z-axis is zero. Figure shows variation of potential with x coordinate. It implies that there should be
An infinite long line charge parallel to z-axis at x=2a with linear charge density λ=3V0ε02a
An infinite large sheet parallel to yz plane at x=2a with surface charge density σ=V0ε02a
An infinite large sheet parallel to yz plane at x=2a withh surface charge density σ=V0ε0a
An inifinite large sheet parallel to yz plane at x=2a with surface charge density σ=3V0ε02a
The correct Answer is:D
x<2a E=V02a
x≥2a E=V0a
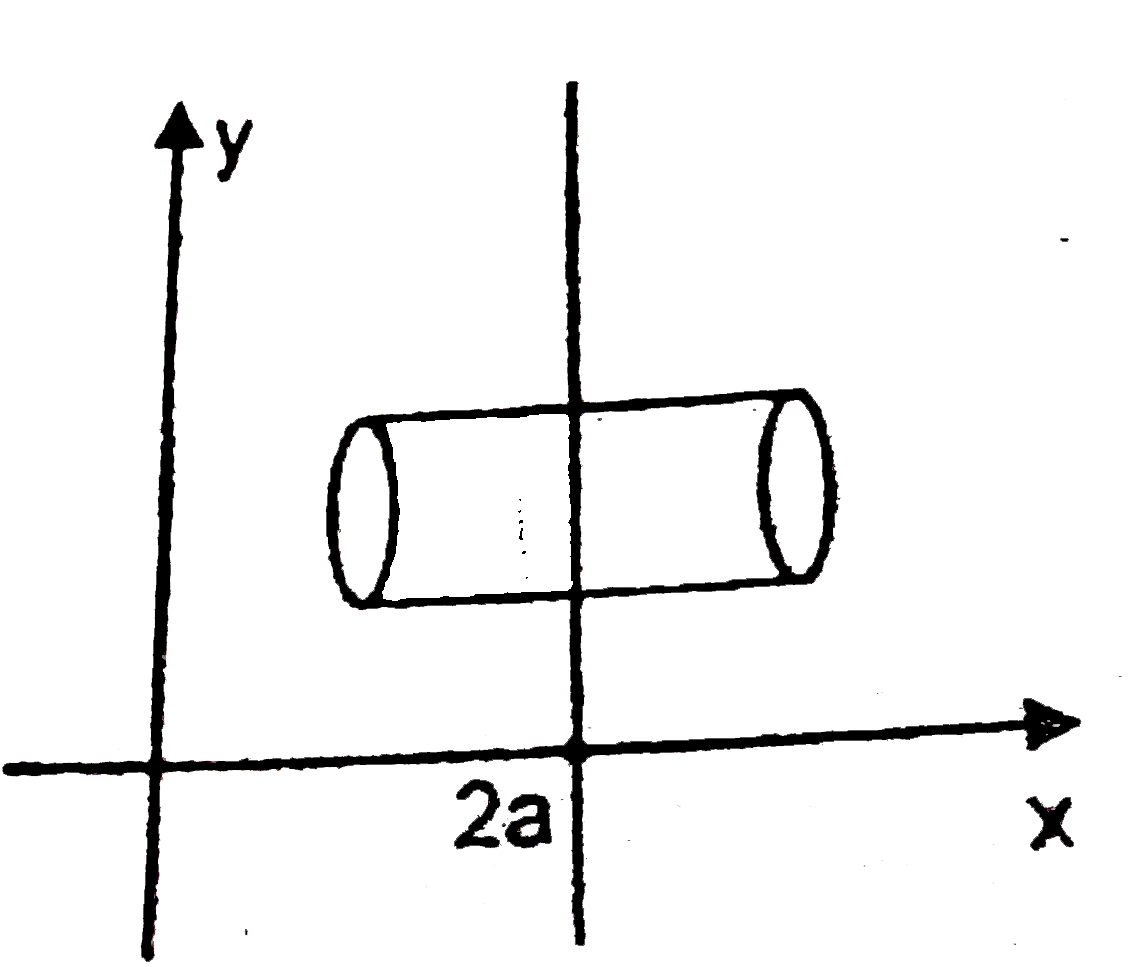
Gauss law for cylindrical
V02aA+V0aA=σAε0
σ=3V0ε02a
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 107 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
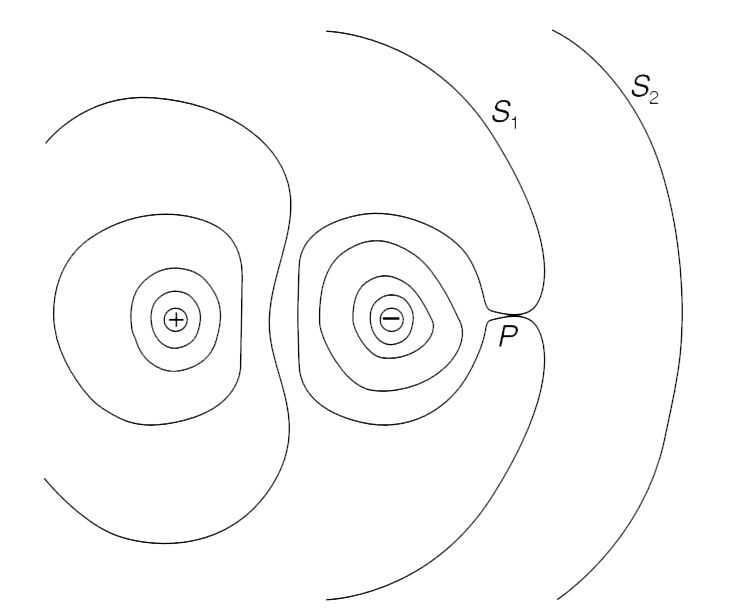
Three point charge have been placed along the x axis at points A, B and C. Distance AB = BC. The field lines generated by the system is shown in figure. (a) Plot the variation of electric potential along x axis. Show potential on y axis of your graph. (b) Plot the variation of electric potential along y axis with B as origin. Shows potential on x axis in your graph.
View SolutionShow that the electric field intensity at a point can be given as negative of potential gradient.
View Solution
Knowledge Check
An electric field →E=20yˆj exist in space . The potential at (5 m, 5 m) is taken to be zero. The potential at origin is
A500 VB250 VC125 VDZeroThe slope of the graph showing the variation of potential difference V on X-axis and current Y-axis gives conductor
AresistanceBresistivityCreciprocal of resistanceDconductivityTwo identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by
A B
B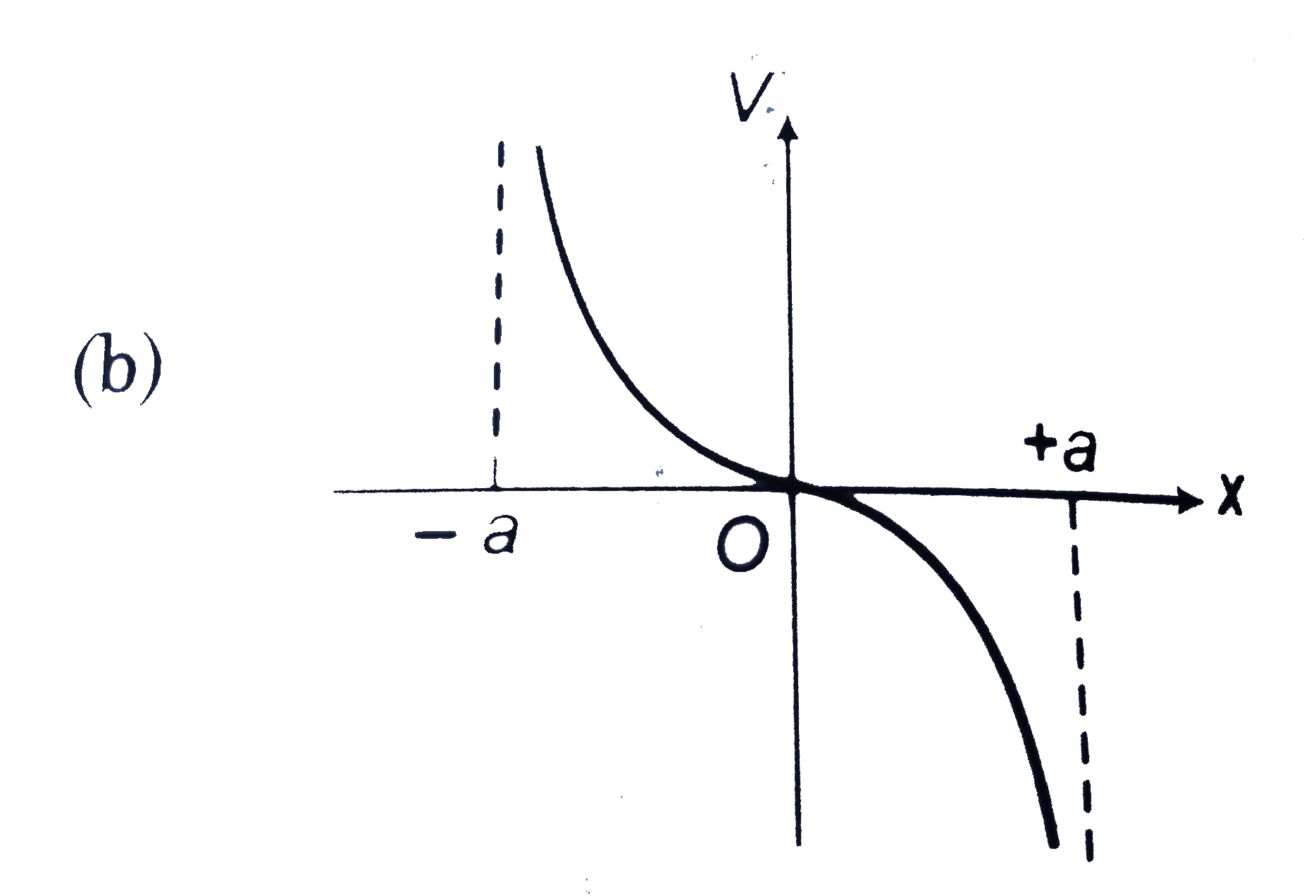 C
C D
D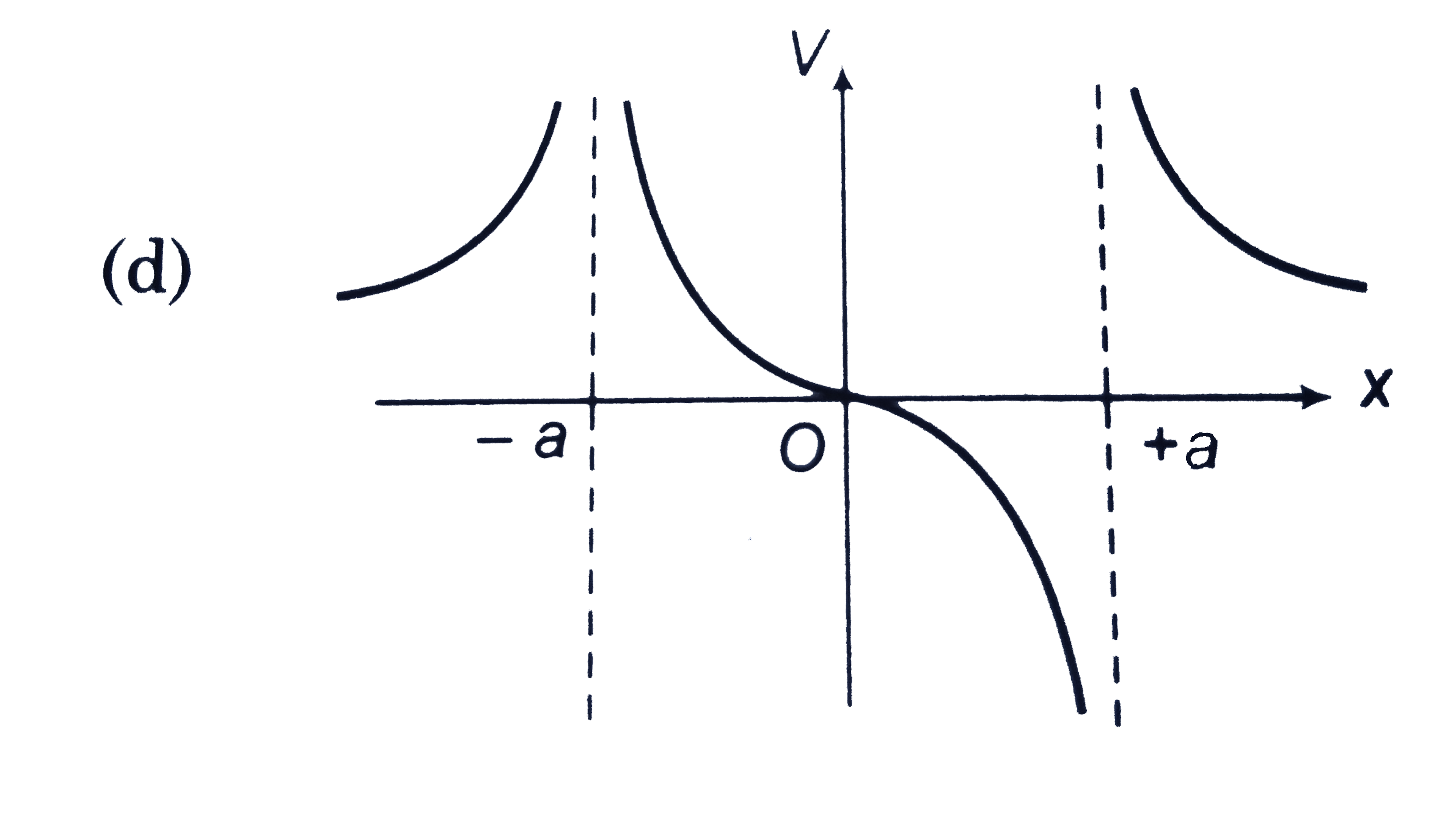
An electric field (−30ˆi+20j){V}{m}−{t} exists in space. If the potential at the origin is zero, then find the potential (in volt) at (5m,3m).
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA unifrom electric field having a magnitude E0 and direction along the positive X-axis exists. If the protential V is zero at x=0, then its value at X=+x will be
View SolutionAssume that an electric field →E=30x2ˆj exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionIn an electric field region, the electric potential varies along the x-axis as shown in the graph. The x components of the electirc field in the regions for the intervals PQ and QR as market in the garph, in N/C, are respectively:

View Solution