The reflecting surface of a plane mirror is vertical. A particle is projected in a vertical plane which is also perpendicular to the mirror. The initial speed of the particle is 10m/s and the angle of projection is 60∘ from the normal of the mirror. The point of projection is at a distance 5m from the mirror. The particle moves towards the mirror. Just before the particle touches the mirror, the velocity of approach of the particle and the image is:

(Vi,m)x=−(VO,m)x
(Vi−Vm)x=−(VO−Vm)x
Vix−O=V⊗
Vix=−5m/s
Vapp=5−(−5)=10m/s
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 107 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A light incident on a plane mirror subtends an angle of 60∘ from the surface of mirror. The angle of reflection is __________________.
View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View Solution
Knowledge Check
A particle approaches from very large distance towards concave mirror along the principal axis. By the time the particle reaches the mirror the distance between the particle and its image will
Afirst increases then decreasesBfirst decreases then increasesCfirst decreases then decreases then again increasesDfirst decreases then increases then again decreaseTwo particles A and B are projected in same vertical plane as shown in figure.Their initial positions (t=0), initial spped and angle of projections are indicated in the diagram.If initial angle of projection θB=37∘, what should be initial speed of projection of particle B, so that it hits particle A.UA=60m/s
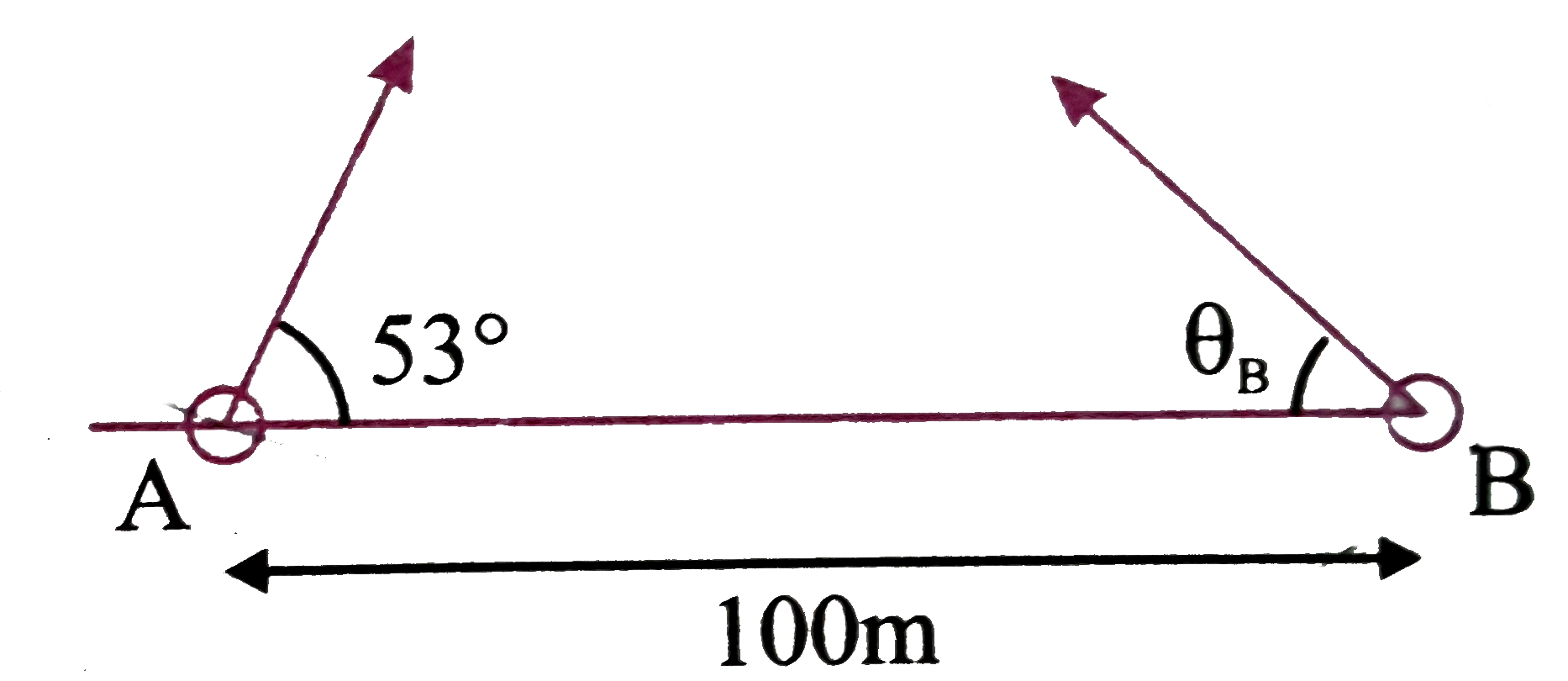 A80m/sB75m/sC40m/sD45m/s
A80m/sB75m/sC40m/sD45m/s
If an object moves towards a plane mirror with a speed v at an angle θ to the perpendicular to the plane of the mirror, find the relative velocity between the object and the image.AvB2vC2vcosθD2vsinθ
A particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
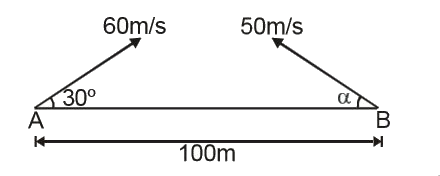
View SolutionA particle is projected from the ground with an initial speed of 5ms−1 at an angle of projection 60° with horizontal. The average velocity of the particle between its time of projection and the time it reaches highest point of trajectory
View SolutionA pole of height 1 . 8 m stands in front of a larger vertical plane mirror . The distance of the image from the pole at a distance of 1 . 5 m from the mirror is
View Solution

