Find the dimensions of the rectangle of perimeter 36cm which will sweep out a volume as large as possible when revolved about one of its sides.
Video Solution
Text Solution
Let the length and breadth of the rectangle be x and y.
2x+2y=36
⇒x+y=18
⇒y=18−x
V=πx2y
=πx2(18−x)
∴V=π(18x2−x3)
On differentiating, we get
dVdx=π(36x−3x2)
Put dVdx=0
⇒π(36x−3x2)=0
⇒x=12
y=18−12
⇒y=6
On differentiating, we get
d2Vdx2=π(36−6x)
(d2Vdx2)x=12=π(36−6(12))=−36π<0 ( maxima )
So, the dimensions of rectangle are x=12cm,y=6cm.
Maximum volume of resultant cylinder is,
V=π[18(12)2−(12)3]
∴V=864πcm3
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the dimensions of the rectangle of perimeter 36cm which will sweep out a volume as large as possible when revolved about one of its sides.
A10,8B11,7C12,6DNoneThe locus of a rectangle, when the rectangle is rotated about one of its sides is a ______
AplineBsphereCconeDcylinderFind the perimeter of a square, each of whose sides measures 3.6 cm.
A=14.4cmB=24.4cmC=34.4cmD=12.4cm
Find the breadth of the rectangle if its length is 70 cm and perimeter is 200 cm
View SolutionIn Fig. 9.44 a rectangle with perimeter 264 cm is divided into five congruent rectangles. Find the perimeter of one of the rectangles.
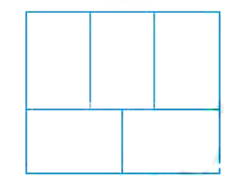
View Solutionadjcent sides of a rectangle are 3.6cm and 1.5cm .Find the length of the diagonal
View Solution(3) The ratio of length of breadth of rectangle is 3:1 and its perimeter is 36cm Find the length , breadth of the rectangle.
View SolutionThe sides of a triangle are in the ratio 1:2:3. If the perimeter is 36 cm, find its sides.
View Solution

