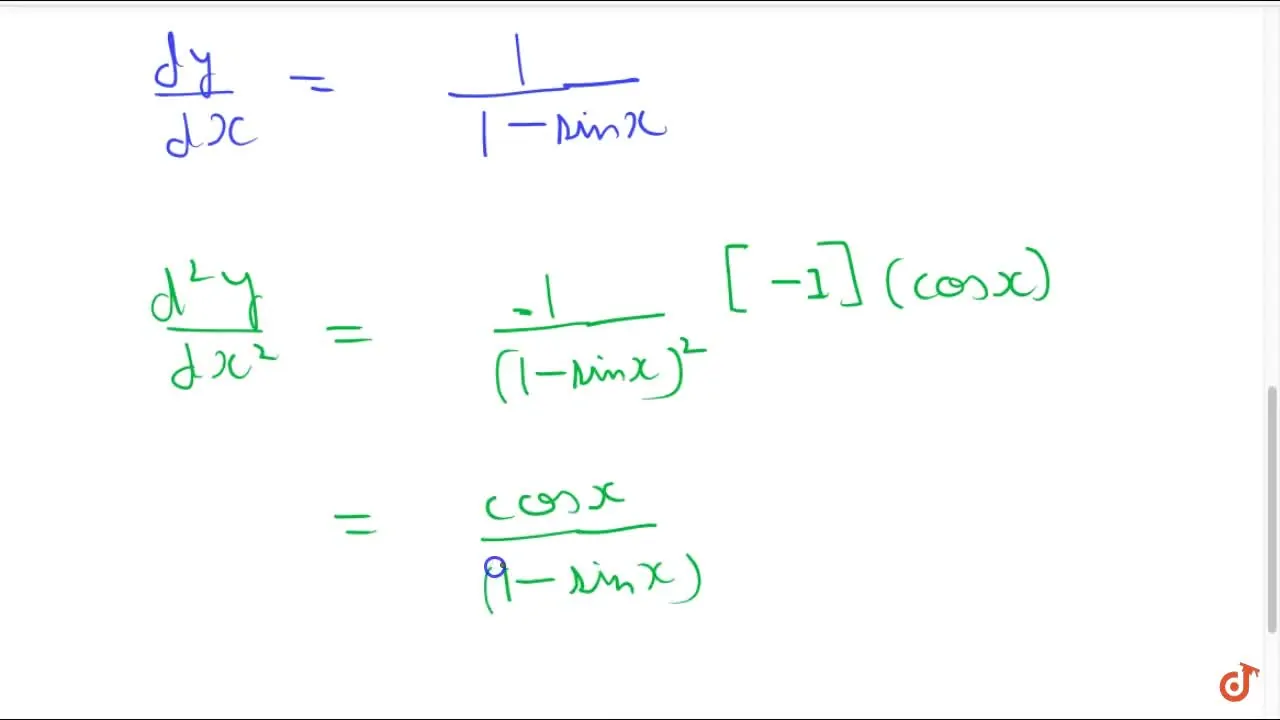If y=tanx+secx , prove that d2ydx2=cosx(1−sinx)2
Video Solution
Text Solution
We have given
y=tanx+secx
Then we have to prove that d2ydx2=cosx(1−sinx)2
y=sinxcosx+1cosx
y=1+sinxcosx
differentiate with respect to x
dydx=ddx(1+sinxcosx)
dydx=cosxddx(1+sinx)−(1+sinx)ddxcosxcos2x
dydx=cos2x+sinx+sin2xcos2x
dydx=1+sinxcos2x
dydx=1+sinx1−sin2x
dydx=1+sinx(1+sinx)(1−sinx)
dydx=11−sinx
differentiate with respect to x
ddx(dydx)=ddx(11−sinx)
d2ydx2=(1−sinx)ddx(1)−(1)ddx(1−sinx)(1−sinx)2
d2ydx2=cosx(1−sinx)2
Hence Proved
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If y=(tanx+secx), prove that d2ydx2=cosx(1−sinx)2
View SolutionIf y=5cosx−3sinx , prove that d2ydx2+y=0 .
View SolutionSolve: d2ydx2=cosx−sinx
View SolutionIf y=5cosx−3sinx then prove that d2ydx2+y=0
View SolutionIf y=1−tanx1+tanx, prove that dydx=−21+sin2x.
View SolutionIf y=2sinx+3cosx, prove that : y+d2ydx2=0
View SolutionIf y=etanx then prove that:
cos2xd2ydx2−(1+sin2x)dydx=0View SolutionIf y=5sinx−3sinx, prove that : d2ydx2+y=0.
View SolutionIf y=(sinx)(sinx)(sinx)...∞, prove that dydx=y2cotx(1−ylogsinx).
View SolutionIf y=(x)cosx+(sinx)tanx, prove that dydx=xcosx{cosxx−(sinx)logx}+(sinx)tanx.{1+(logsinx)sec2x}.
View Solution