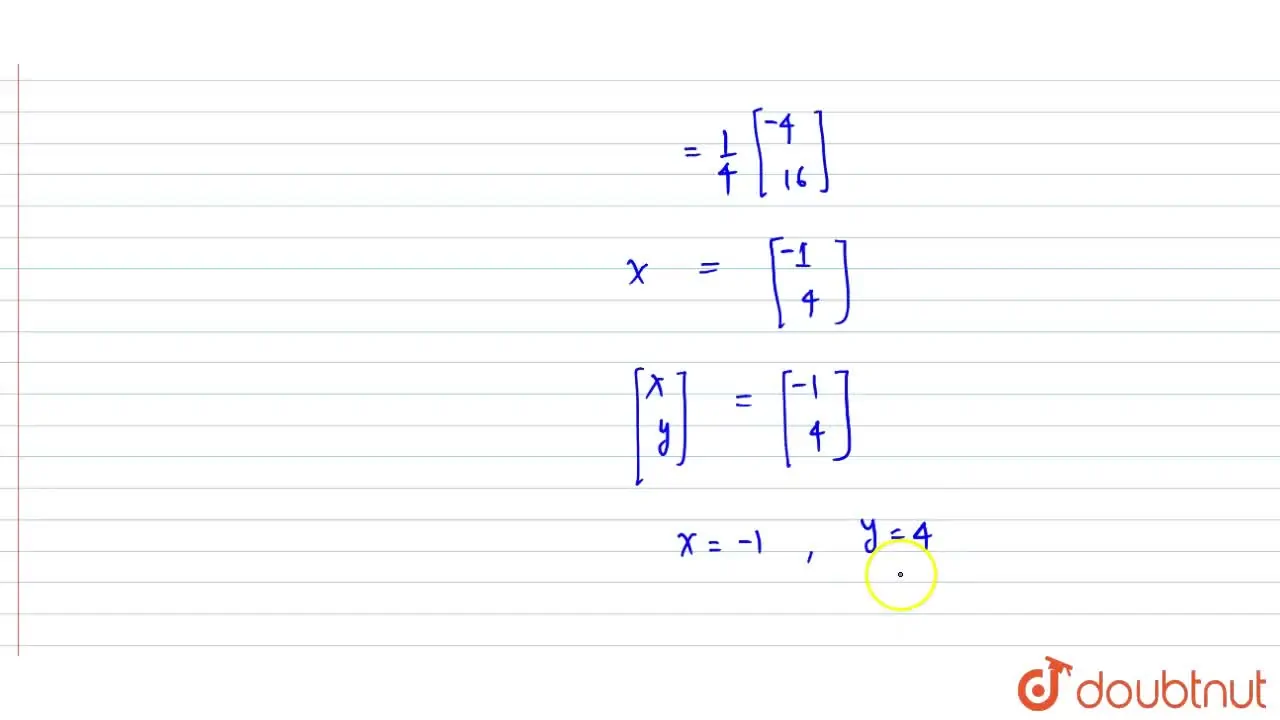Solve the following system of equations by matrix method: 5x+2y=3, 3x+2y=5
We have given
5x+2y=3
3x+2y=5
We can write them in matrix from AX=B....(i)
[5232][xy]=[35]
Determinant of matrix A,
∣∣∣A∣=∣∣∣5232∣∣∣
∣A∣=10−6=4≠0
So, A−1exists.
To find adjoint of matrix A we first find cofactors
C11=2,C12=−3,C21=−2,C22=5
Then matrix formed by adjoint of A is
B=[2−3−25]
adj.A=BT=[2−3−25]T=[2−2−35]
Therefore,A−1=(adjA|A|)=(14)[2−2−35]
Then from equation (i)
X=A−1B
[xy]=(14)[2−2−35][35]
=(14)[6−10−9+25]
=(14)[−14]
=[xy]=[−14]
Hence x=−1, and y=4
Related Playlists
Similar Questions
Solve the following system of equations by matrix method: 3x+y=19, 3x−y=23
View SolutionSolve the following system of equations by matrix method: 3x+y=7, 5x+3y=12
View SolutionSolve the following system of equations by matrix method: 3x+7y=4, x+2y=−1
View SolutionSolve the following system of equations by matrix method: 3x+4y−5=0, x−y+3=0
View SolutionSolve the following system of equations by matrix method: 5x+7y+2=0, 4x+6y+3=0
View SolutionSolve the following system of equations by matrix method: x+y+z=3, 2x−y+z=−1, 2x+y−3z=−9
View SolutionSolve the following system of equations by matrix method :
3x−4y=5 and 4x+2y=3View SolutionSolve the following system of linear equations by matrix method: 3x−2y=7,5x+3y=1
View SolutionSolve the following system of equations by matrix method : 5x+7y+2=0 4x+6y+3=0 5x+2y=3 3x+2y=5 3x+4y−5=0 x−y+3=0 3x+y=19 3x−y=23 3x+7y=4 x+2y=−1 3x+y=7 5x+3y=12
View SolutionSolve the following system of equations by matrix method: 5x+3y+z=16,2x+y+3z=19,x+2y+4z=25
View Solution