A standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
The energy density of a node is equal to energy density of an antinode for the first time at t=T/4
The energy density of node and antinode becomes equal after T/2 second
The displacement of the particle at antinode at t=T8 is √2A
The displacement of the particle at node is zero
The correct Answer is:C, D
Equation of SHM of particle who is at antinode is y=2Asin(2πT)t at time t=T8
y=2Asin(π)4=√2A, Displacement of particle at note is always zero.
Topper's Solved these Questions
Similar Questions
The graphs show the standing wave on a string at two successive instants of time t1,t2.A,B,C are points on the string (S_(0) is the maximum displacement amplitude of the standing wave) column-II gives observations about net mechanical energy for the time interval between t_(1) & t_(2) Match the column
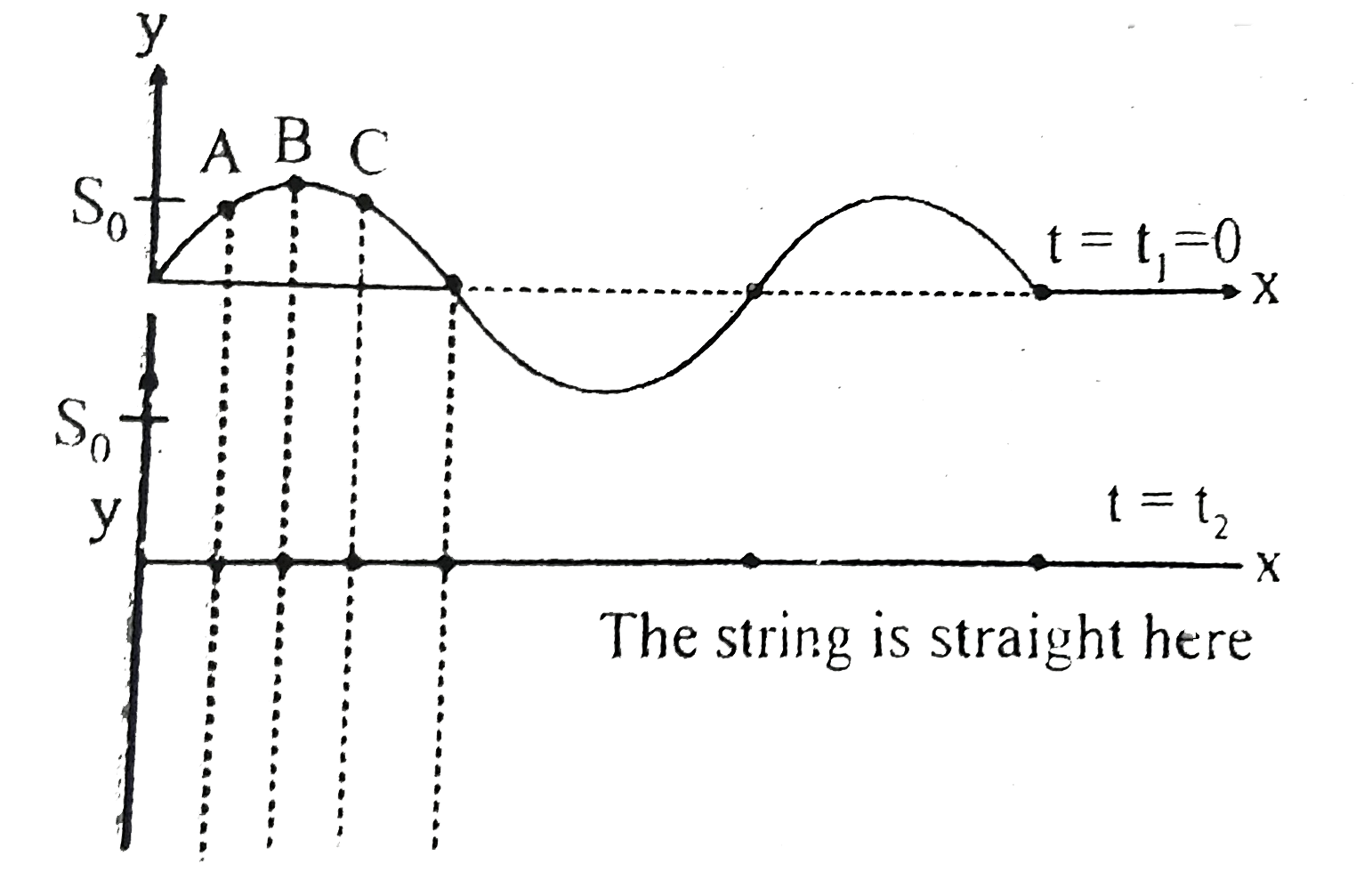
Column-IColumn-II(A)A(P)kinetic energy at this element is increasing(B)B(Q)Energy is flowing towards right through this point(C)C(R)Energy is flowing left through this point(S)No net energy ever crosses this point
View SolutionA string of linear mass density 5.0×10−3 kg//m is stretched under a tension of 65 N between two rigid supports 60 cm apart.
(a) If the string is vibrating in its second overtone so that the amplitude at one of its antinodes is 0.25 cm, what are the maximum transverse speed and acceleration of the string at antinodes?
(b) What are these quantities at a distance 5.0 cm from an node?
View Solution
Knowledge Check
A standing wave having 3 nodes and 2 antinodes are formed between two rigid supports of length 1m. Then the wavelength of the standing wave is
A0.5mB1.0mC0.75mD0.25mA metal bar of length L and area of cross-section A is clamped between two rigid supports. For the material of the rod. It Young's modulus is Y and Coefficient if linear expansion is α. If the temperature of the rod is increased by Δt∘C, the force exerted by the rod on the supports is
A2π2YTB2πr2YαTCπr2YLTDπr2YαTThe length of a string tied between two rigid supports is 50 cm. The maximum wavelength of a stationary wave produced on it is
A25 cmB75 cmC100 cmD125 cm
The equation of standing wave in a stretched string is given by {y=2sin[π2(x)]cos(20πt)} where x and y are in meter and t is in second. Then minimum separation between two particle which are at the antinodes and having same phase will be
View SolutionShow that all harmonics are present on a stretched string between two rigid supports.
View SolutionA string is vibrating in its fifth overtone between two rigid supports 2.4 m apart. The distance between successive node and antinode is
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
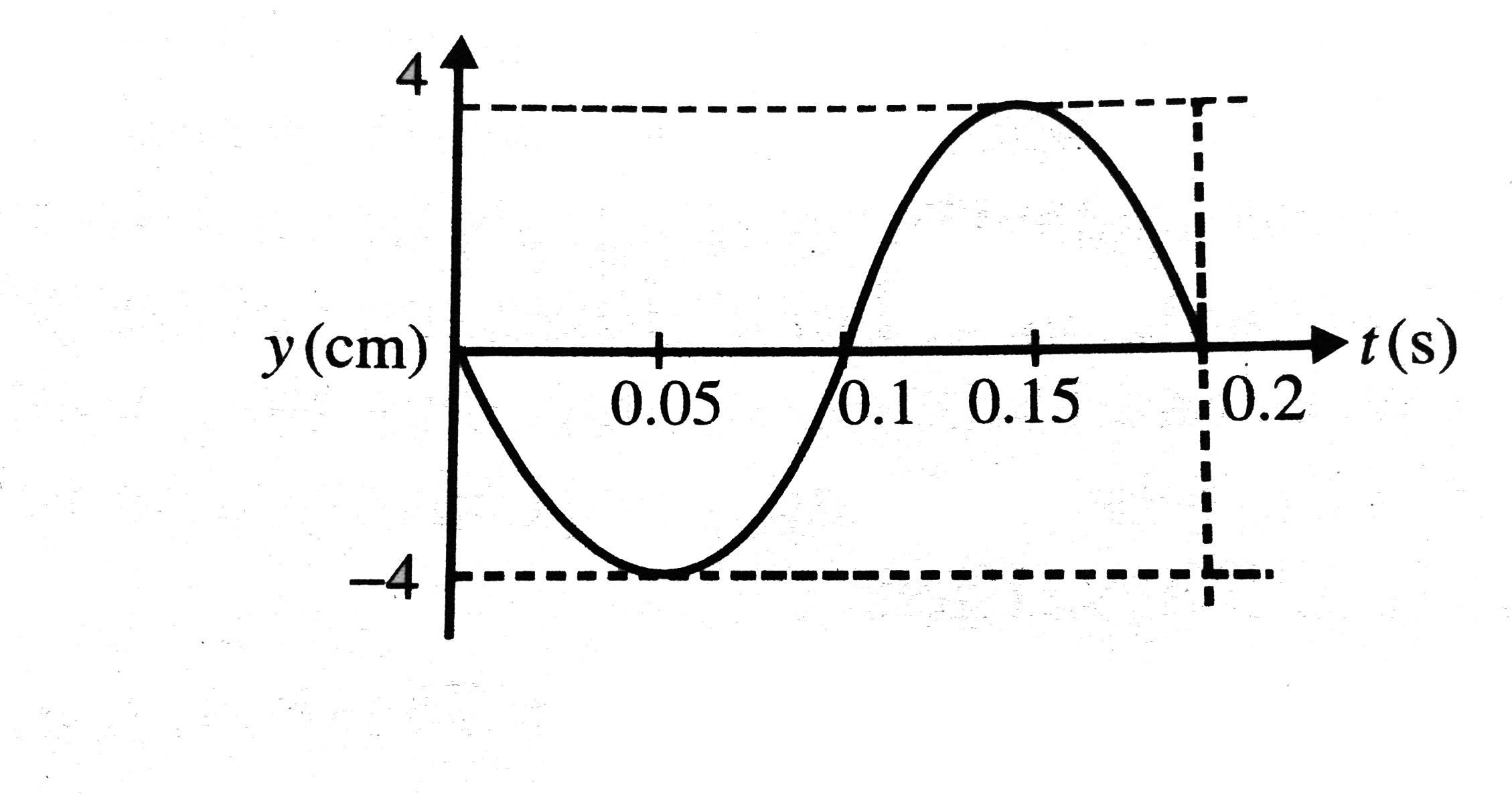
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x = 0 and the other is at x=l. When string vibrates in fundamental mode, amplitude of the midpoint O of the string is a, tension in a, tension in the string is T and amplitude of vibration is A. Find the total oscillation energy stored in the string.
View Solution

