A string of linear mass density 5.0×10−3 kg//m is stretched under a tension of 65 N between two rigid supports 60 cm apart.
(a) If the string is vibrating in its second overtone so that the amplitude at one of its antinodes is 0.25 cm, what are the maximum transverse speed and acceleration of the string at antinodes?
(b) What are these quantities at a distance 5.0 cm from an node?
The correct Answer is:A, B, C, D
(a) In second overtone,
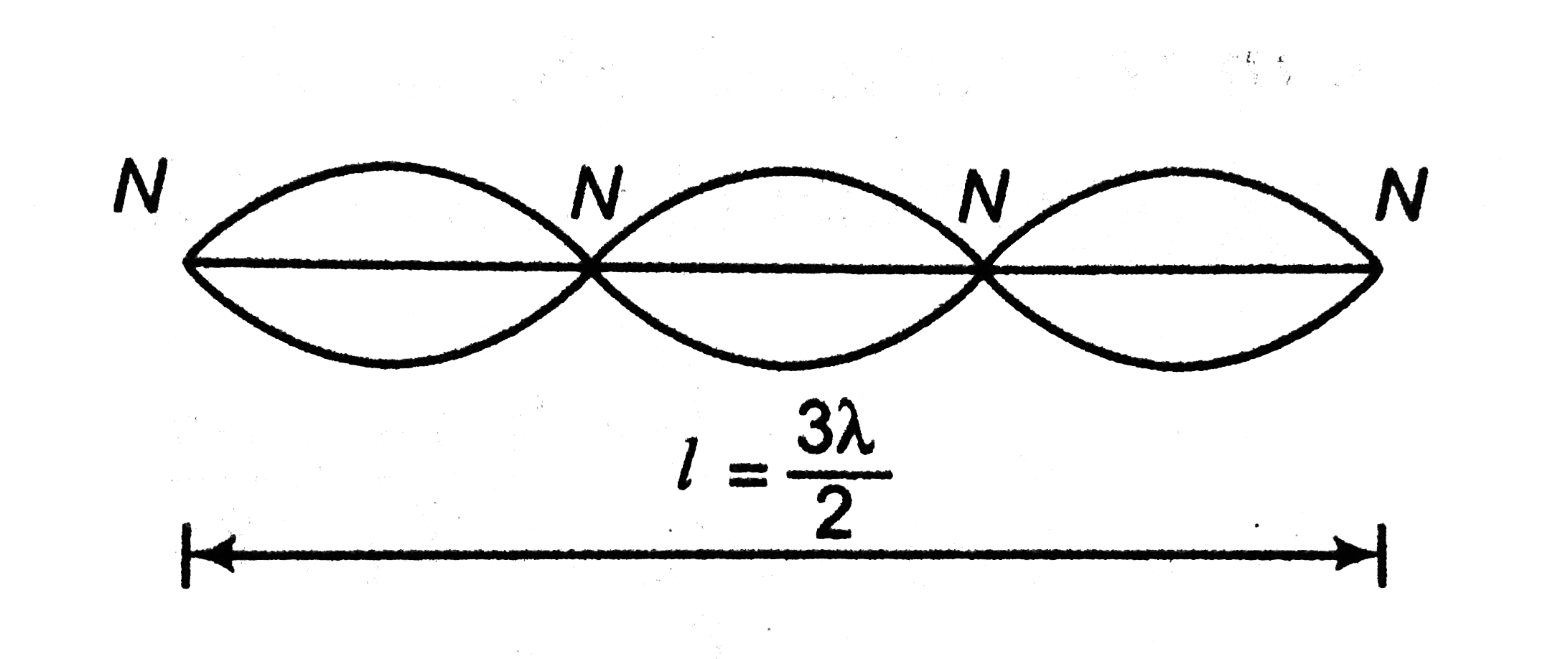
l=3λ2
or λ=2l3=2×603
=40cm=0.4m
k=2πλ=2π0.4=5πm−1
v=√Tμ=√655.0×10−3
=114m/s
ω=kv=570πrad/s
Maximum transverse speed at antinode=A0ω
Here, A0=amplitude of antinode=0.25cm=2.5×10−3m
∴ Maximum speed=(2.5×10−3)(570π)m/s
=4.48m/s
Maximum acceleration =w2A0
=(570π)2(2.5×10−3)m/s2
=8.0×103m/s2
(b) At a distance x from the node, the amplitude can be written as
A=A0sinkx=(2.5×10−3)sin(5πx)metre
Here, x is in metres.
Therefore, at =x=5.0cm=5.0×10−2m
A=(2.5×10−3)sin(5π×5.0×102)
=1.8×10−3m
Maximum speed=Aω
=(1.8×(10−3))(570π)m/s
=3.22 m/s
and maximum acceleration =ω2A
=(570π)2(1.8×(10−3))m/s2
=5.8×(103)m/s2 .
Similar Questions
A tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0.01kgm−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0.50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string ?
View SolutionFigure shows different standing wave patterns on a string of linear mass density 4.0×10−2kg/m under a tension of 100 N. The amplitude of antinodes is indicated in each figure. The length of the string is 2.0m.
(i) Obtain the frequencies of the modes shown in figures (a) and (b).
(ii)Write down the transverse displacement y as a function of x and t for each mode. (Take the initial configuration of the wire in each mode to be as shown by the dark lines in the figure).

View Solution
Knowledge Check
A string of length 0.5m and linear density 10−4 kg/m is stretched under a tension of 100 N. If the frequency of the vibration of the string is 4000 Hz, how many loops are formed on the string?
A1B4C2D6A string of mass per unit length 0.2 kg m−1 and length 0.6 m is fixed at both ends such that it has a tension of 80 N. If the string is vibrating in its second overtone mode, then the frequency of the string is
A40 HzB50 HzC60 HzD70 HzA string is vibrating in its fifth overtone between two rigid supports 2.4 m apart. The distance between successive node and antinode is
A0.1 mB0.2 mC0.6 mD0.8 m
A string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of density 7.5gcm−3 and area of cross section 0.2mm2 is stretched under a tension of 20 N. When it is plucked at the mid point, the speed of the transverse waves on the wire is
View SolutionA string of density 7.5gcm−3 and area of cross section 0.2mm2 is stretched under a tension of 20 N. When it is plucked at the mid point, the speed of the transverse waves on the wire is
View SolutionThe amplitude of a transverse wave on a string is 4.5 cm. The ratio of the maximum particle speed to the speed of the wave is 3:1. What is the wavelengtlı (in cm) of the wave?
View SolutionIn the fundamental mode of vibration on a stretched string, the number of antinodes are
View Solution

