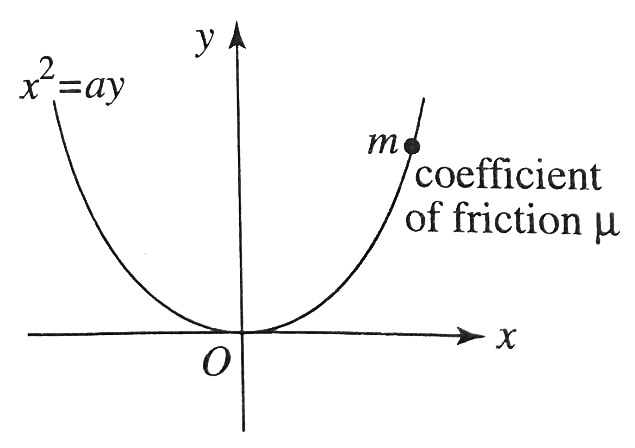
A bead of mass m is located on a parabolic wire with its axis vertical

A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is $x^{2} = a y$ . If the coefficient of friction is $μ$ , the highest distance above the x-axis at which the particle will be in equilibrium is
A $μ a$
B $μ^{2} a$
C $\frac{1}{4} μ^{2} a$
D $\frac{1}{2} μ a$
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is $x^{2} = 4 a y$ . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :

A $\frac{g}{2}$
B $(\sqrt{3} g) (2)$
C $\frac{g}{\sqrt{2}}$
Dg
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is $x^{2} = 4 a y$ . The wire frame is fixed and the bead is released from the point $y = 4 a$ on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by $y = a$ is

A $\frac{g}{2}$
B $\frac{\sqrt{3} g}{2}$
C $\frac{g}{\sqrt{2}}$
Dg

A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is $x^{2} = a y$ . If the coefficient of friction is $μ$ , the highest distance above the x-axis at which the particle will be in equilibrium is