If the point (5,2) bisects the intercept of a line between the axes, then its equation is 5x+2y=20 b. 2x+5y=20 c. 5x−2y=20 d. 2x−5y=20
To find the equation of the line that has its intercept bisected by the point (5, 2), we can follow these steps:
Step 1: Understand the problem
The point (5, 2) bisects the intercepts of a line with the x-axis and y-axis. This means that the x-intercept and y-intercept of the line are equidistant from the point (5, 2).
Step 2: Set up the intercept form of the line
The intercept form of a line can be expressed as:
xa+yb=1
where a is the x-intercept and b is the y-intercept.
Step 3: Find the coordinates of the intercepts
Let the x-intercept be a and the y-intercept be b. The coordinates of the intercepts are:
- X-intercept: (a,0)
- Y-intercept: (0,b)
Step 4: Use the midpoint formula
Since (5, 2) bisects the intercepts, we can use the midpoint formula:
(a+02,0+b2)=(5,2)
This gives us two equations:
1. a2=5
2. b2=2
Step 5: Solve for a and b
From the first equation:
a=10
From the second equation:
b=4
Step 6: Write the equation of the line
Now substituting a and b back into the intercept form:
x10+y4=1
Multiplying through by 40 (the least common multiple of 10 and 4) to eliminate the denominators:
4x+10y=40
Step 7: Rearranging the equation
Rearranging gives:
2x+5y=20
Final Answer
Thus, the equation of the line is:
2x+5y=20
The point (5, 2) bisects the intercepts of a line with the x-axis and y-axis. This means that the x-intercept and y-intercept of the line are equidistant from the point (5, 2).
The intercept form of a line can be expressed as:
xa+yb=1
where a is the x-intercept and b is the y-intercept.
Let the x-intercept be a and the y-intercept be b. The coordinates of the intercepts are:
- X-intercept: (a,0)
- Y-intercept: (0,b)
Since (5, 2) bisects the intercepts, we can use the midpoint formula:
(a+02,0+b2)=(5,2)
This gives us two equations:
1. a2=5
2. b2=2
From the first equation:
a=10
From the second equation:
b=4
Now substituting a and b back into the intercept form:
x10+y4=1
Multiplying through by 40 (the least common multiple of 10 and 4) to eliminate the denominators:
4x+10y=40
Rearranging gives:
2x+5y=20
Thus, the equation of the line is:
2x+5y=20
Topper's Solved these Questions
Similar Questions
The equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is (A) 9x-20y+96=0(B)9x+20y=24(C)20x+9y+53=0 (D) None of these
View Solutionfind the length of intercepts made by the line 5x+4y=20
View Solution
Knowledge Check
Angle between the tangents to the curve y=x2−5x+6 at the points (2,0) and (3,0) is
Aπ2Bπ3Cπ6Dπ4
Find the length of intercepts cuts on axes from the line 4x−5y=20.
View SolutionThe equation of the line bisecting the obtuse angle between y−x−2and√3y+x=5 is
View SolutionWhich of the folowing should be the feasible region of the system of linear lnequalities x + 2y ≤12,2x+y≤12,4x+5y≥20 and x,y≥0 ?
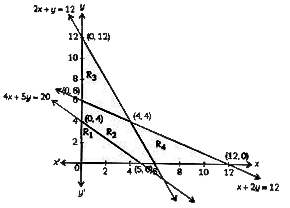
View SolutionSolve the simultaneous equations graphically. 5x−6y+30=0,5x+4y−20=0
View SolutionDistance between the parallel lines 4x2+20xy+25y2+2x+5y−12=0
View SolutionFind the equation if the line through the intersection of lines x+2y−3=0and4x−y+7=0 and which is parallel to 5x+4y−20=0
View SolutionIf the distance from P to the points (5,-4),(7,6) are in the ratio 2:3 ,then the locus of P is
5x2+5y2−12x−86y+17=0,
5x2+5y2−34x+120y+29=0,
5x2+5y2−5x+y+14=0
3x2+3y2−20x+38y+87=0
View Solution

