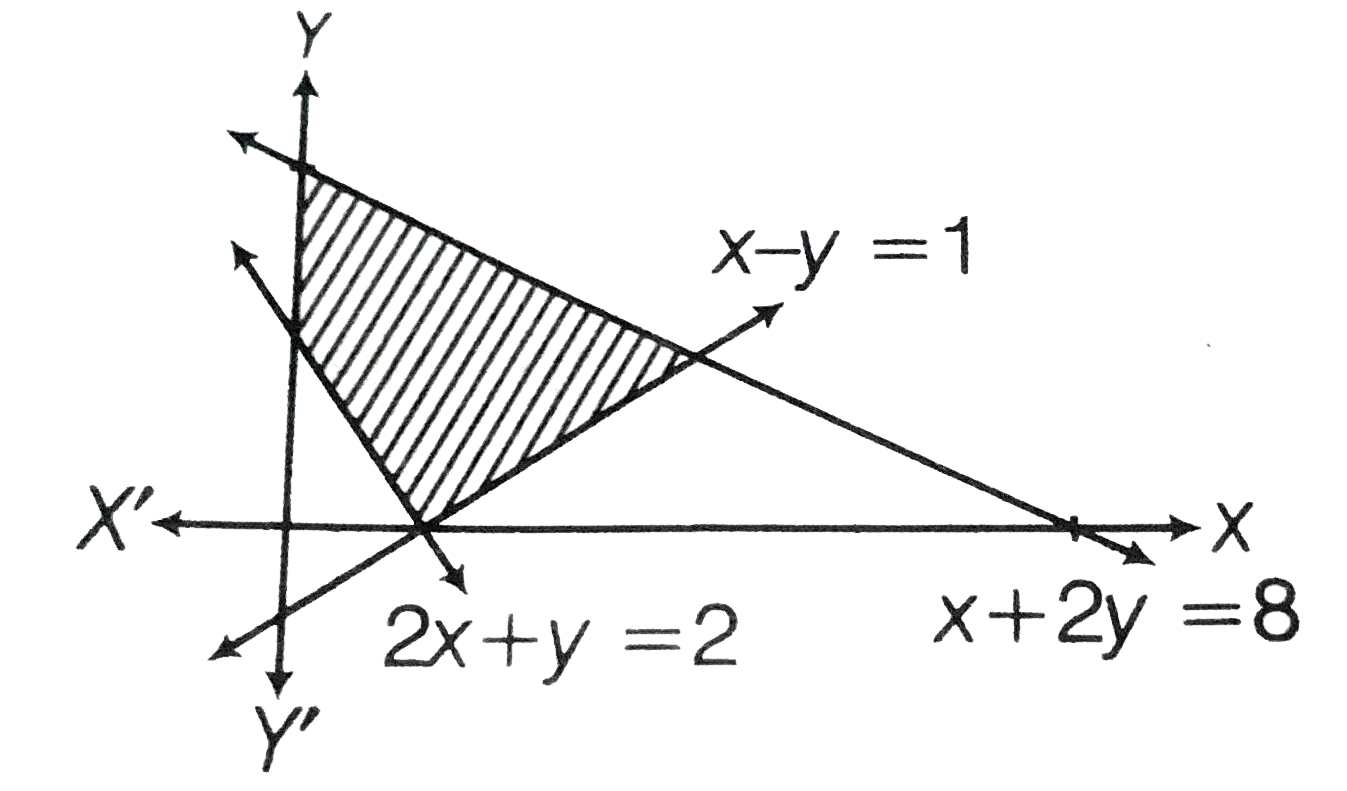
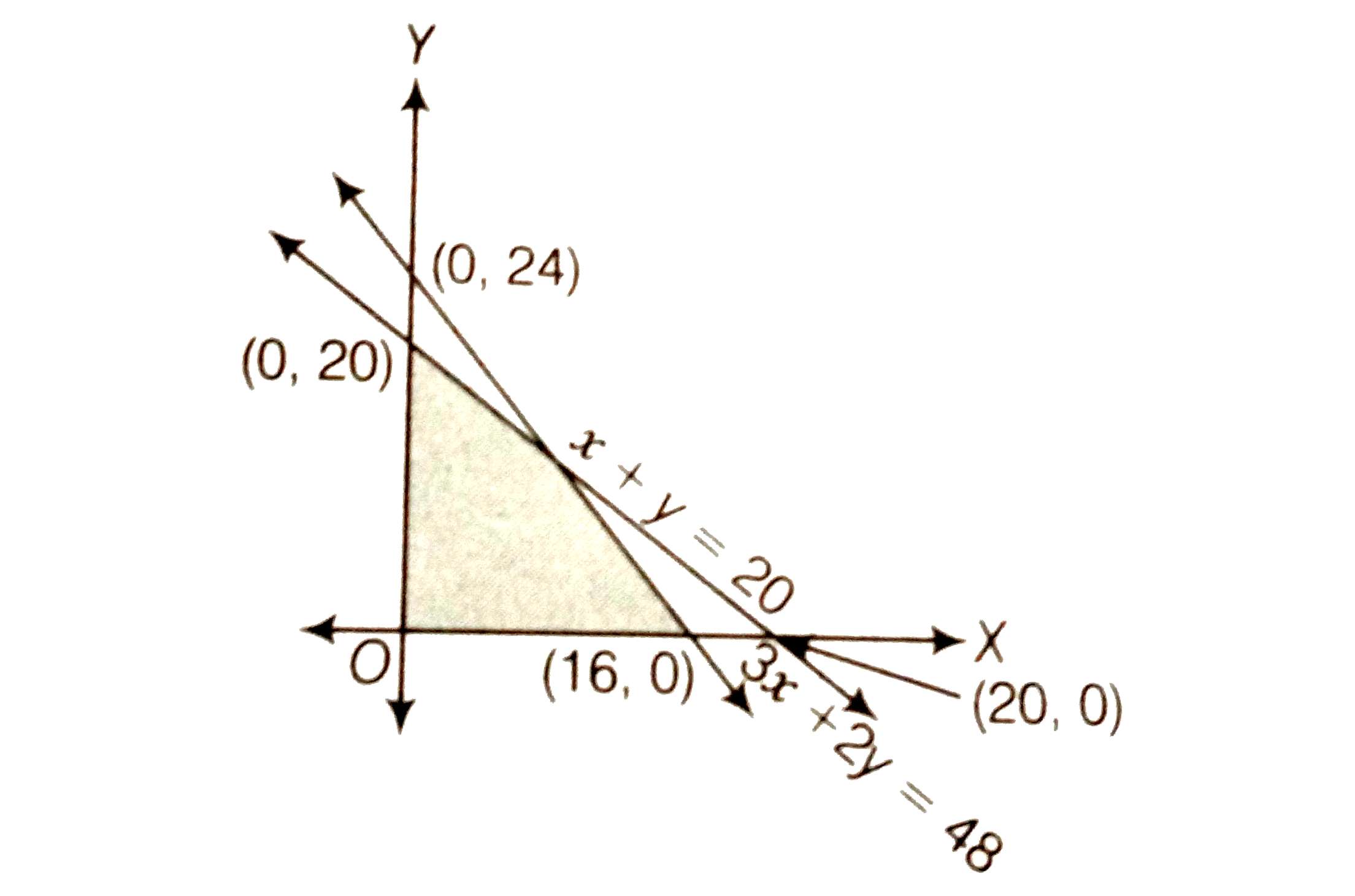
Find the linear inequations for which the shaded region in fig. 15.40 is the solution set.
Video Solution
Text Solution
We have seen that the shaded region and origin are on the same side of the line 3x + 4y = 12.
For (0,0) we have 0 + 0 - 12 < 0. So the shaded region satisfies the inequality 3x + 4y ≤ ≤12.
We have seen that the shaded region and origin are on the same side of the line 4x + 3y =12 For (0,0) we have 0 + 0 -12 < 0.
So the shaded region satisfies the inequality 4x + 3y ≤ ≤12.
Also , the region lies in the first quadrant
Therefore x ≥ ≥ 0 and y ≥ ≥0
Thus the linear inequation comprising the given solution set are +4y ≤12, 4x + 3y ≤ 12, x ≥ 0, y ≥0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
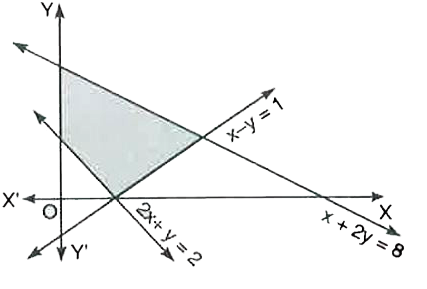
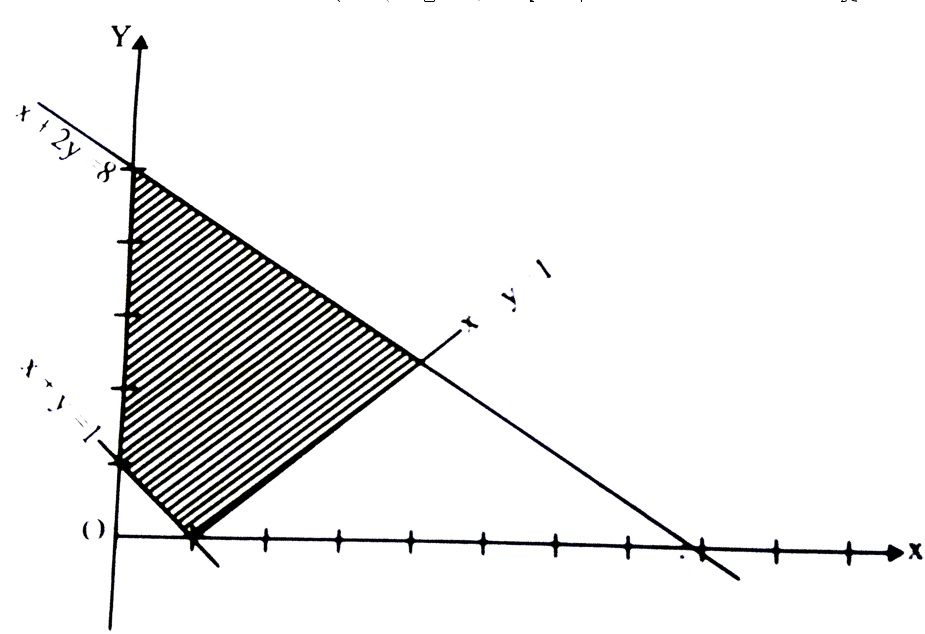
Find the linear constraints for which the shaded area in the figure below is the solution set:
 A
A
2x+y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.B
2x−y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.C
2x+y≤2,x−y≤1,x+2y≤8,x≥0,y≥0.D
2x+y≥2,x−y≥1,x+2y≤8,x≥0,y≥0.Find the linear constraints for which the shaded area in the following figure is the solution set:
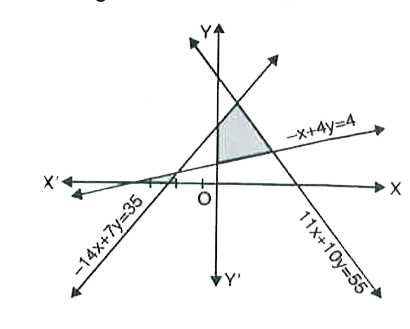
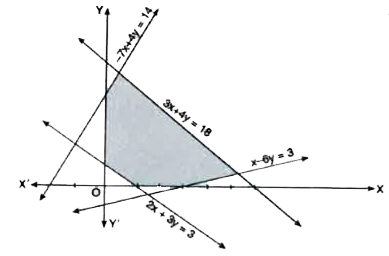 A2x+3y≥3,x−6y≤3,−7x+4y≤14,3x+4y≤18,x≥0,y≥0B2x+3y≤3,x−6y≤3,−7x+4y≥14,3x+4y≤18,x≥0,y≥0C2x+3y≤3,x−6y≤3,−7x+4y≤14,3x+4y≤18,x≥0,y≥0D2x+3y≤3,x−6y≤3,−7x+4y≤14,3x+4y≥18,x≥0,y≥0
A2x+3y≥3,x−6y≤3,−7x+4y≤14,3x+4y≤18,x≥0,y≥0B2x+3y≤3,x−6y≤3,−7x+4y≥14,3x+4y≤18,x≥0,y≥0C2x+3y≤3,x−6y≤3,−7x+4y≤14,3x+4y≤18,x≥0,y≥0D2x+3y≤3,x−6y≤3,−7x+4y≤14,3x+4y≥18,x≥0,y≥0
Find the linear equations for which the shaded area in Fig: 15.39 is the solution set.
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
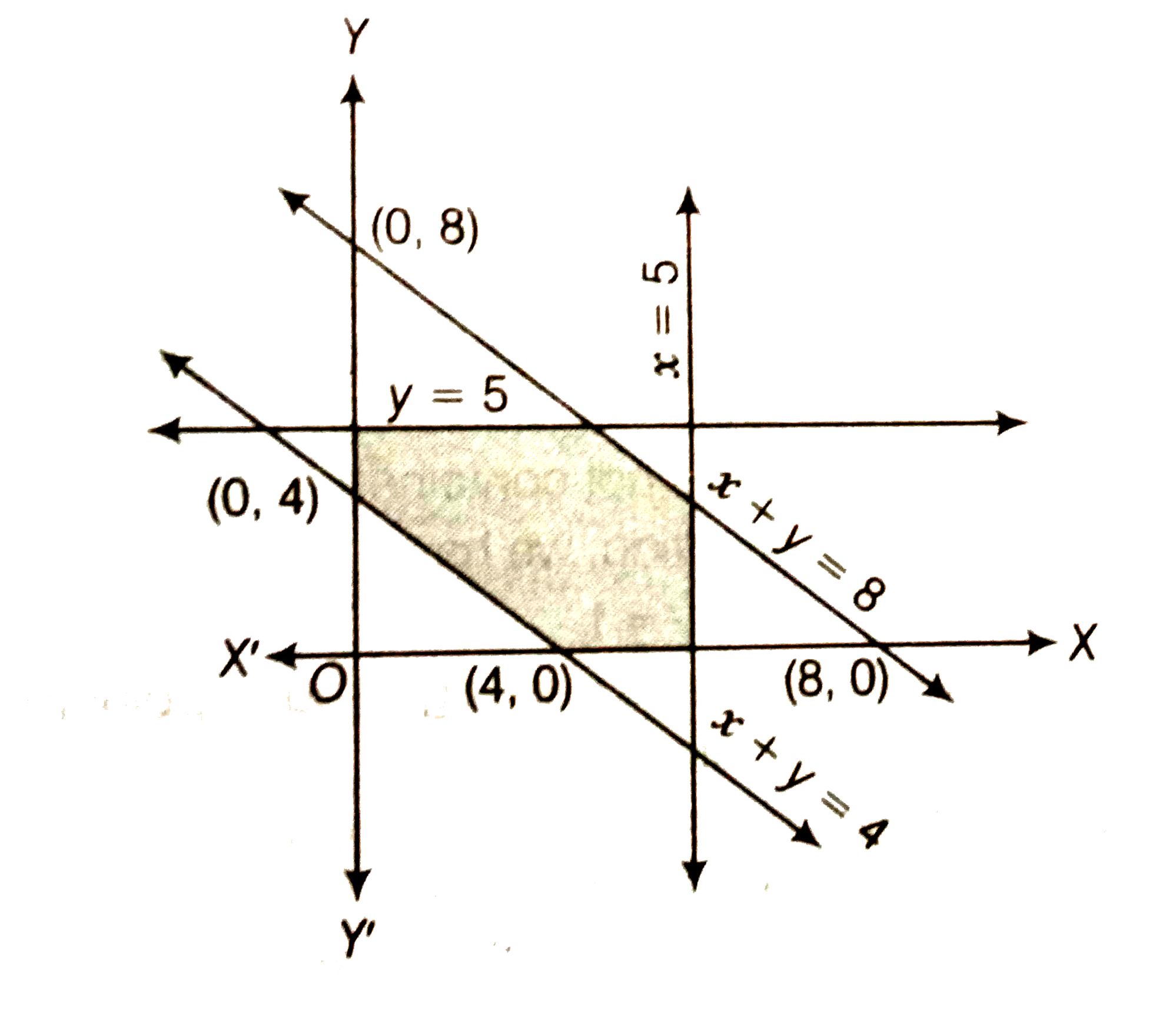
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
View Solution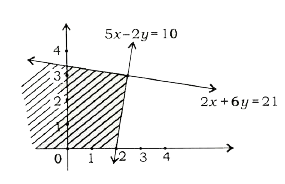
The linear inequations, for which the shaded area in the figure given above is the solution set, are
View SolutionFind the linear constraints for which the shaded area in the following figure is the solution set:
View SolutionWhat are the linear constraints for which the shaded area in the above figure is the solution set ?
View Solution