Find the linear equations for which the shaded area in Fig: 15.39 is the solution set.
Video Solution
Text Solution
To find the inequation we see if the shaded region and Origin are on the same side of the line or not.
So,
Considering the line 2x+3y=6, we find that the shaded region and the origin (0,0) are on the opposite side of this line and (0,0) does not satisfy the inequation2x+3y≥6 So, the first inequation is 2x+3y≥6
Considering the line 4x+6y=24, we find that the shaded region and the origin (0,0) are on the same side of this line and (0,0) satisfies the inequation 4x+6y≤24 So, the corresponding inequation is 4x+6y≤24
Considering the line x−2y=2, we find that the shaded region and the origin (0,0) are on the same side of this line and (0,0) satisfies the inequation x−2y≤2 So, the corresponding inequation is x−2y≤2
Considering the line −3x+2y=3, we find that the shaded region and the origin (0,0) are on the same side of this line and (0,0) satisfies the inequation −3x+2y≤3 So, the corresponding inequation is −3x+2y≤3
Also, the shaded region is in the first quadrant. Therefore, we must have x≥0 and y≥0
Thus, the linear inequations comprising the given solution set are given below:
2x+3y≥6, 4x+6y≤24, x−2y≤2, −3x+2y≤3, x≥0 and y≥0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
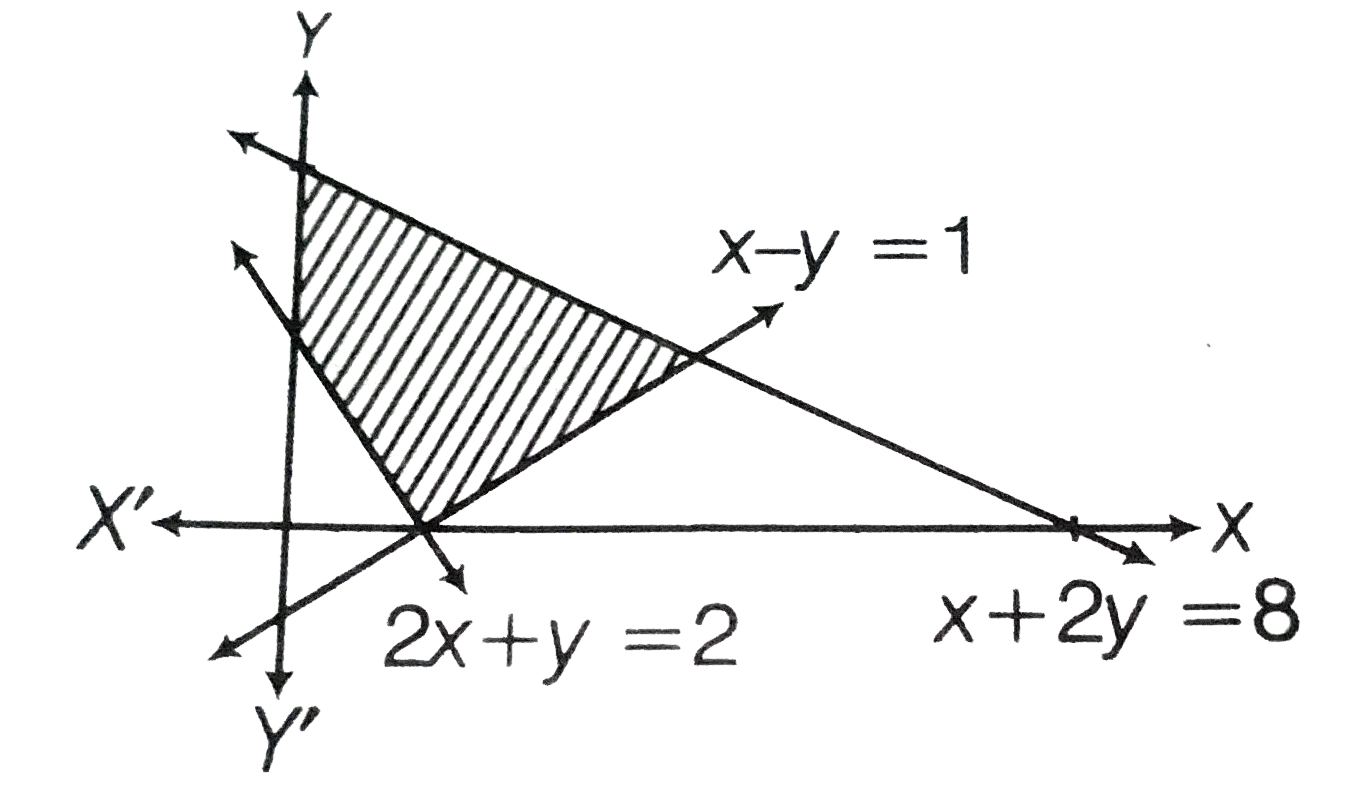
Find the linear constraints for which the shaded area in the figure below is the solution set:
 A
A
2x+y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.B
2x−y≥2,x−y≤1,x+2y≤8,x≥0,y≥0.C
2x+y≤2,x−y≤1,x+2y≤8,x≥0,y≥0.D
2x+y≥2,x−y≥1,x+2y≤8,x≥0,y≥0.
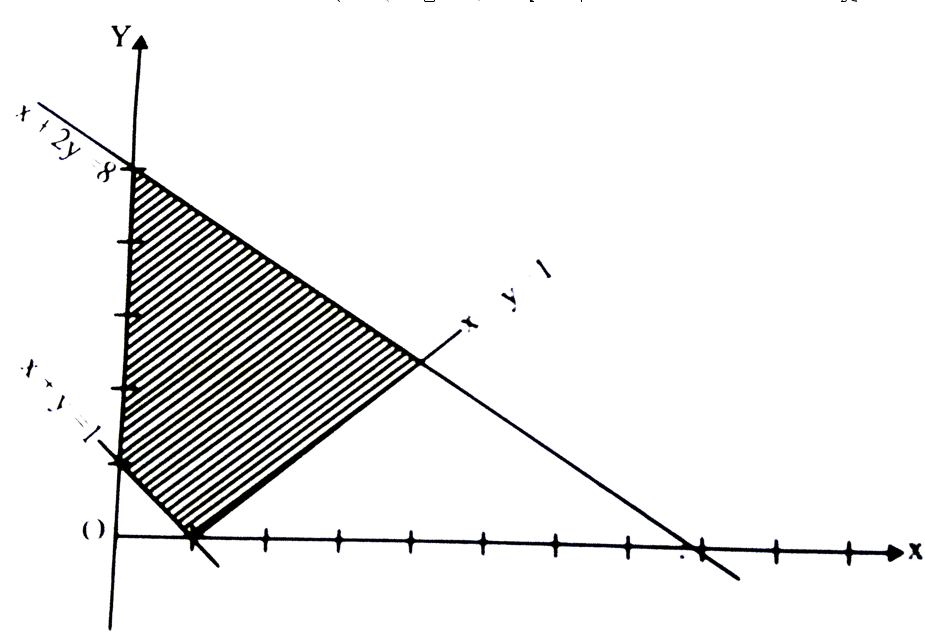
Find the linear inequations for which the shaded area in following figure is the solution set:
View Solutionfind the shaded area
View SolutionWhat are the linear constraints for which the shaded area in the above figure is the solution set ?
View Solutionfind shaded area
View Solution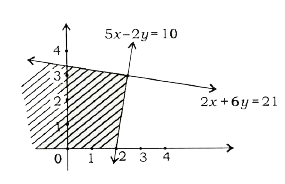
The linear inequations, for which the shaded area in the figure given above is the solution set, are
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
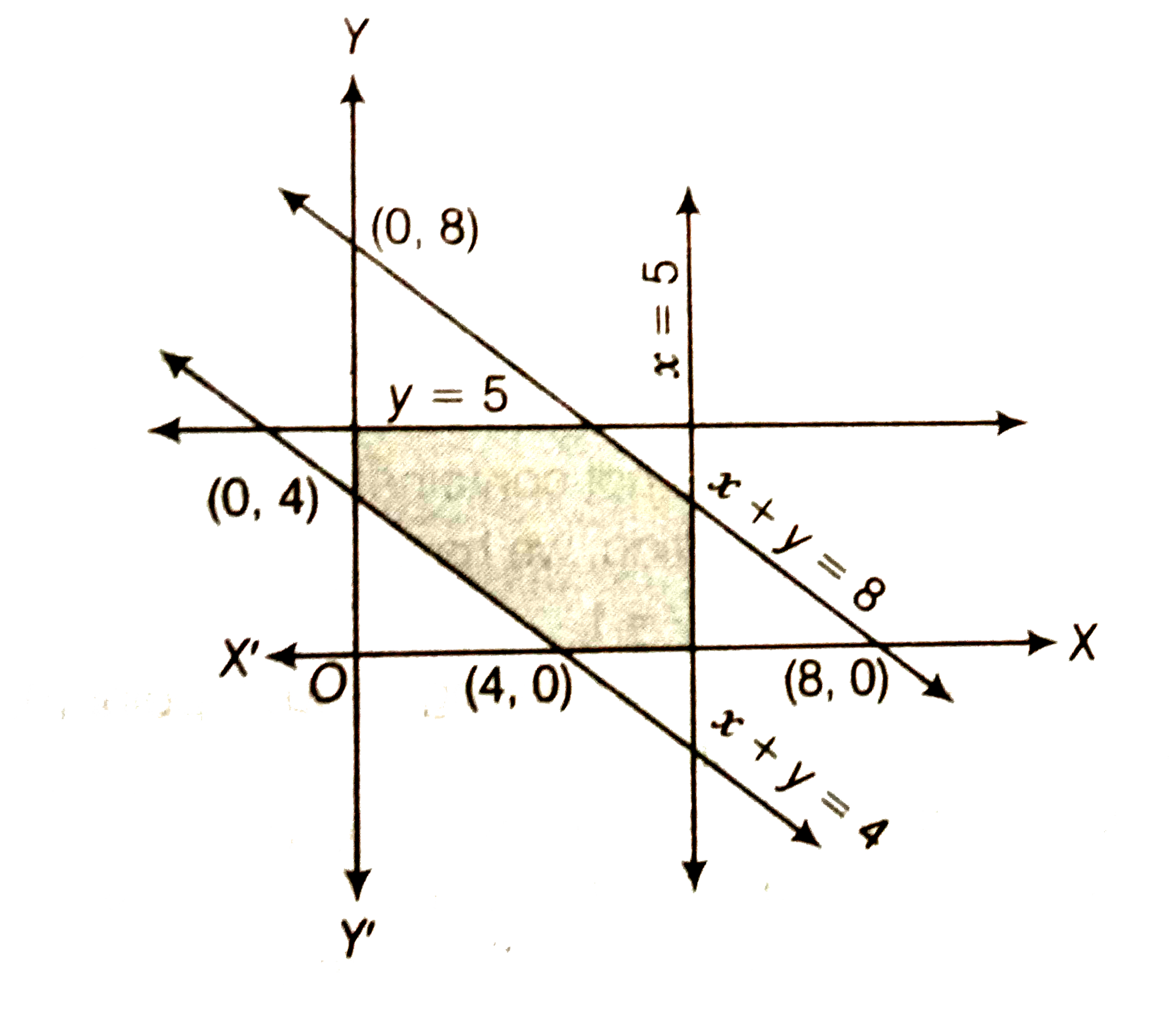
View SolutionFind the linear inequalities for which the shaded region in the given figure is the solution set.
View Solution
