Two balls having masses m and 2m are fasrtened to two light strings of same length (figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. Point A is the lowest point at which either ball can reach
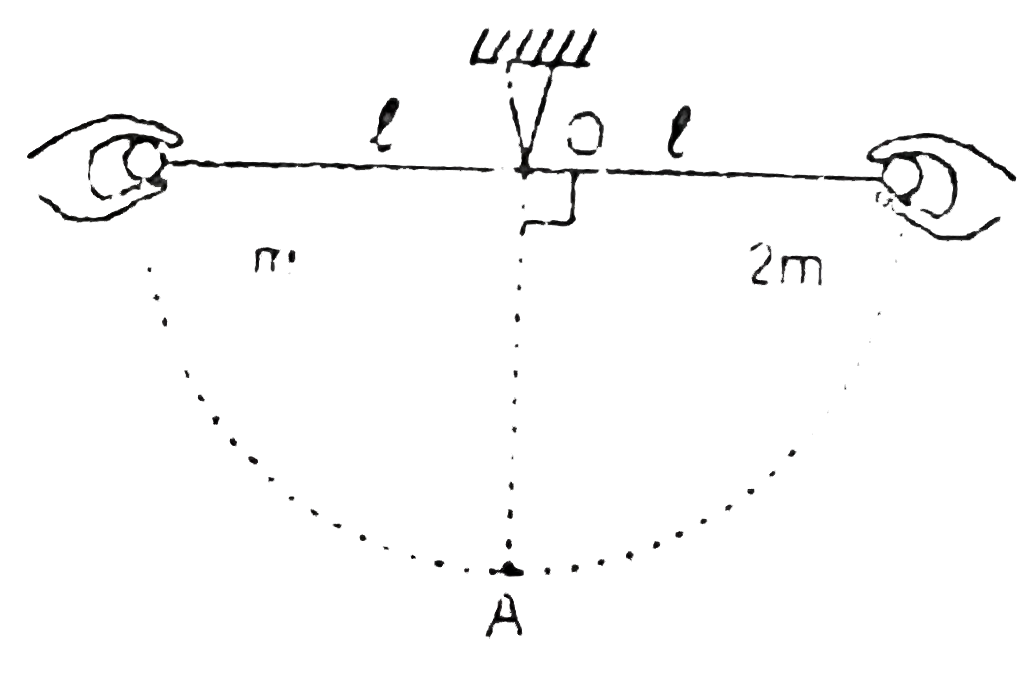
The position at which the balls will collide for the first time
at point A
left of point A
right of point A
None of these
The correct Answer is:A
Initially speed of both balls is zero. Further. Tangential acceleration of both balls at any time are same. Hence before the first time intervals.
Hence both of them shall collide at A,
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.63
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.64
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.61
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Two balls having masses m and 2m are fastened to two light strings of same length l figure. The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. a. Find velocities of the balls just after their collision. b. How high will the balls rise after the collision.

View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View Solution
Knowledge Check
Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MThe masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
Agm/MB2gM/mCgm/2MDg(M2−m2)/2MThe ball is released when the string is horizontal. The collision between the ball and the block is head - on elastic. The velocities of the ball and the block immediately after collision
 A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
A23√2gL,13√2gLB−23√2gL,13√2gLC23√2gL,−13√2gLD−23√2gL,−13√2gL
Two identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

After the first collision, what is the total loss in kinetic energy of the balls?
View SolutionTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

What is the impulse generated in the string during the second collision?
View SolutionA ball of mass m is fastened to a string. The ball swings in a vertical circle of radius R with the other end of the string held fixed. Neglecting the air resistance, the difference between the string's tension at the bottom of the circle and at the quarter of the cirlce is
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View Solution

