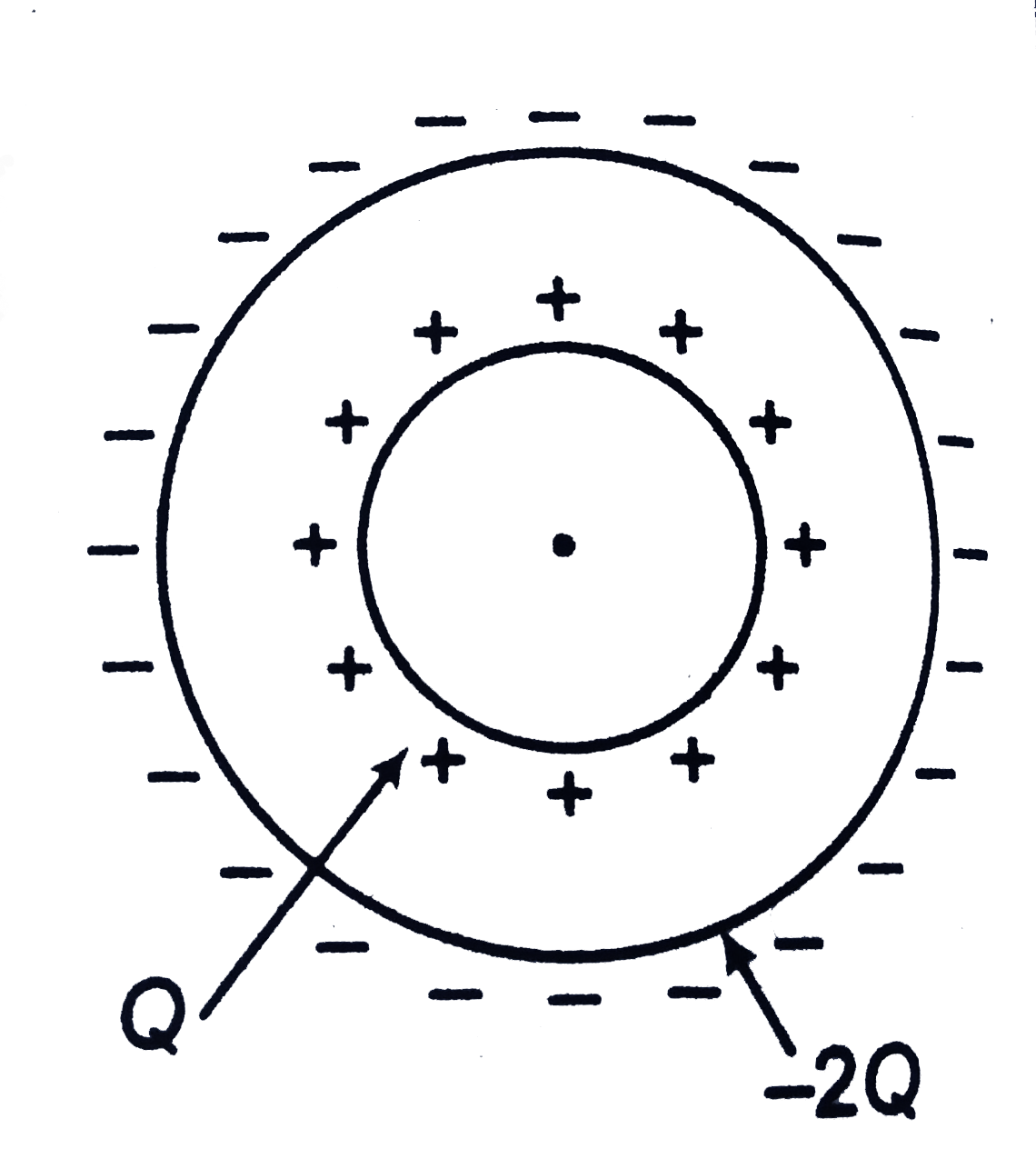
Two conducting spheres of radius R and 3R carry charges Q and $- 2 Q$ . Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :

A

$- \frac{Q}{6}$

B

$- \frac{Q}{3}$

C

$\frac{Q}{3}$

D

$- \frac{Q}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Final potential of spheres will be same
So, $K \frac{x}{R} = \frac{K y}{2 R} = \frac{K (- Q - x - y)}{3 R}$
$y = 2 x$
and $3 x = - Q - x - y$
$∴ 6 x = - Q$
$x = \frac{Q}{6} \Rightarrow y = - \frac{Q}{3}$
Charge on sphere of radius 3R is $- \frac{Q}{2}$
Change in potential energy of sphere of radius 'R' is
$Δ U = \frac{K Q^{2}}{2 r} - \frac{K {(- Q / 6)}^{2}}{2 r} \Rightarrow Δ U = \frac{35 K Q^{2}}{72 R}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two conducting spheres of radius R and 3R carry charges Q and $- 2 Q$ . Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final electric potential of sphere of radius 3R will be :
A $- \frac{k Q}{6 R}$
B $- \frac{k Q}{2 R}$
C $- \frac{2 k Q}{3 R}$
D $- \frac{3 k Q}{R}$
Question 2 - Select One
Two conducting spheres of radius R and 3R carry charges Q and $- 2 Q$ . Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The decrease in electric potential energy of sphere of radius R is :
A $\frac{k Q^{2}}{4 R}$
B $\frac{35 k Q^{2}}{72 R}$
C $\frac{k Q^{2}}{72 R}$
Dnone
Question 3 - Select One
A conducting sphere of radius r has a charge . Then .
Athe charge is uniformly distributed over its surface if there is an external electric field .
BDistribution of charge over its surface will be non uniform if no external electric field exist in space,
CElectric field strength inside the sphere will be equal to zero only when no external electric field exists
DPotential at every point of the sphere must be same

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.41

Home
Ask Doubt
Profile