A particle 'P' is moving on a circular path under the action of only one force action always toward the fixed point 'O' on the circumference. Find the ratio of d2θdt2 & (dθdt)2
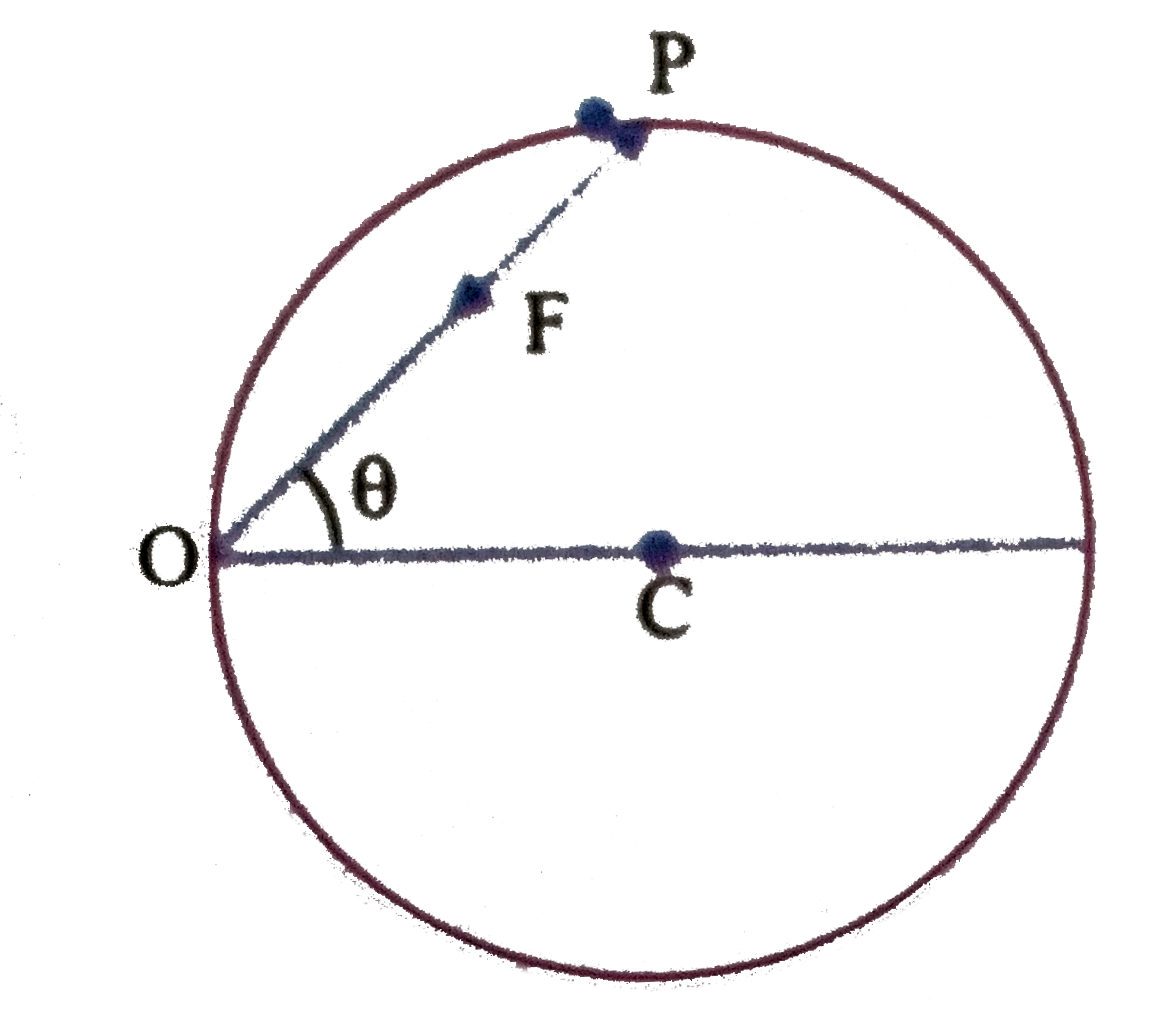
The correct Answer is:2
a1=Fmsinθ⇒Rd2(2θ)dt2=Fmsinθ
d2θdt2=Fsinθ2mR ....(1)
ac=Fmcosθ,R[ddt(2θ)]2=Fmcosθ....(ii)
(d2θdt2)(dθdt)2=2tanθ=2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.43
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.40
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A charged particle is moving in a circular path under the action of the Lorentz force. How much work is done by the force in one revolution?
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
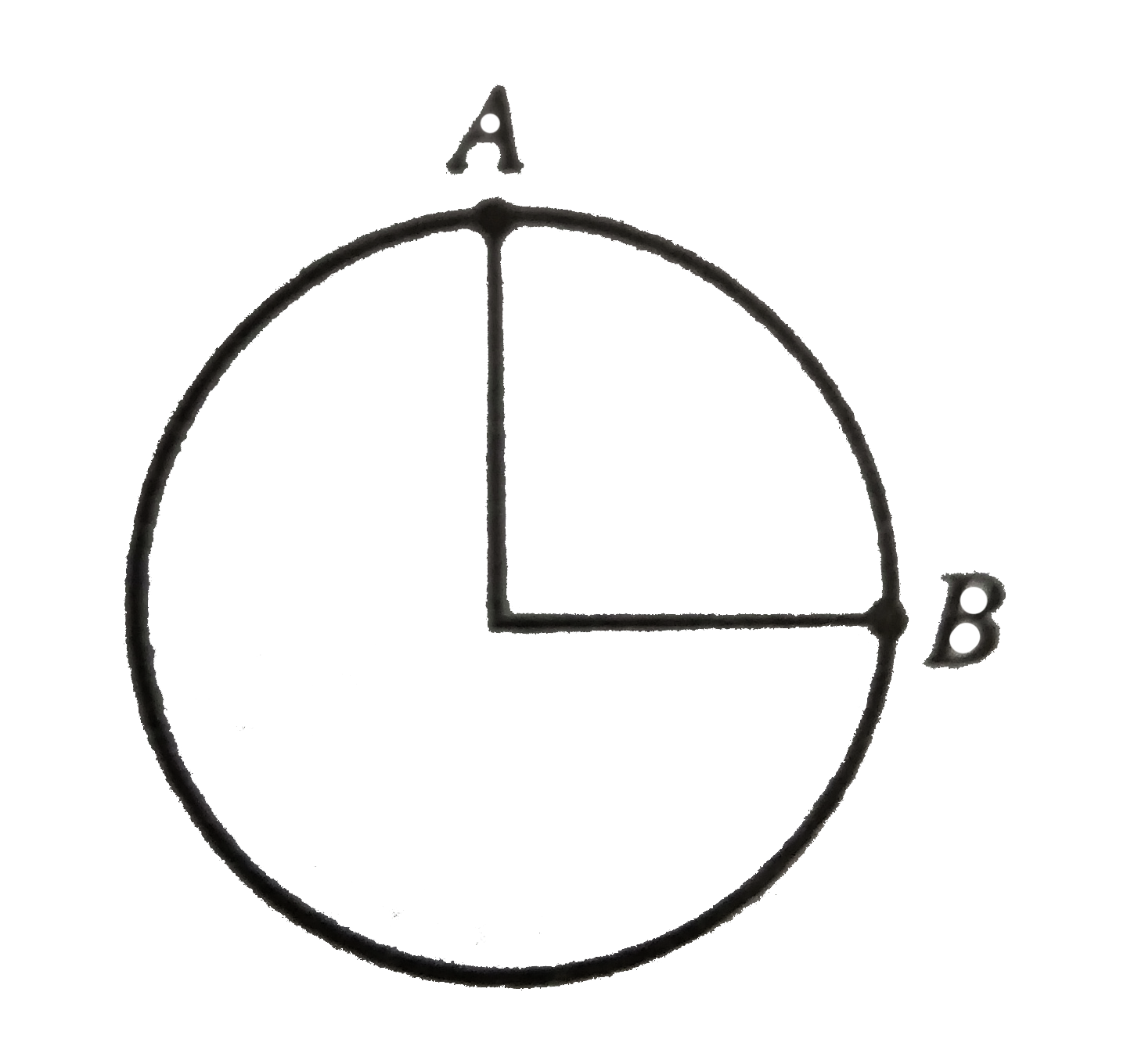
View Solution
Knowledge Check
A particle 'P' is moving on a circular under the action of only one force action always toward the fixed point 'O' on the circumference. Find the ratio of d2θdt2 & (dθdt)2
 A2tanθBtanθCtanθ2Dtanθ3
A2tanθBtanθCtanθ2Dtanθ3A particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
A−32ka2B−k4a2Ck2a2DZeroA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
A→F.→v=0B→F.→c>0C→F.→v<0D→F.→v≥0
Charged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionCharged particle of charge q mass m moves in a circular path of radius r under the action of force F .The equivalent current is
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA particle of mass 'm' moves with a constant speed along a circular path of radius r under the action of a force F .Its speed is given by
View Solution
