A satellite with mass 2000 kg and angular momentum magnitude 2×1012kg.m2/s is moving in an elliptical orbit around a plate. The rate at which area is swept out by the satellite around the planet, is equal to
1×109m2/s
5×109m2/s
5×108m2/s
4×1015m2/s
The correct Answer is:C
dAdt=L2m=2×10122×2000=5×108m2/s
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.34
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.35
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The angular momentum of a planet of mass M moving around the sun in an elliptical orbitis →L. The magnitude of the areal velocity of the planet is :
View Solution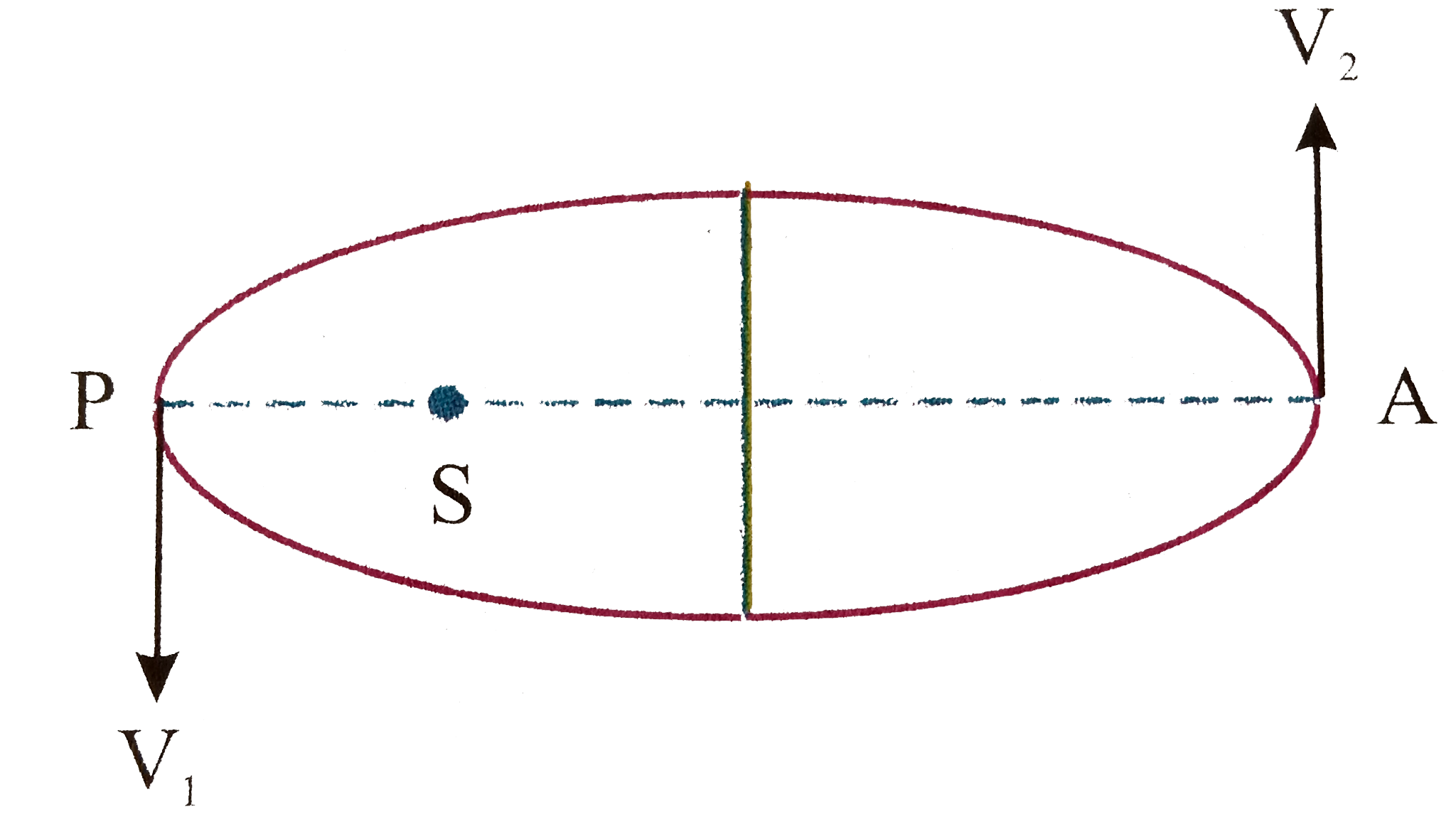
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View Solution
Knowledge Check
A satellite goes along an elliptical path around earth. The rate of change of area swept by the line joining earth and the satellite is proportional to
Ar12BrCr32Dr2A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
AThe acceleration of S is always directin towards the centre of the earth.BThe angular momentum of S about the centre of the earth changes in direction, but its magnitude remains constant.CThe total mechanical energy of S varies periodically with time.DThe linear momentum of S remains constant in magnitde.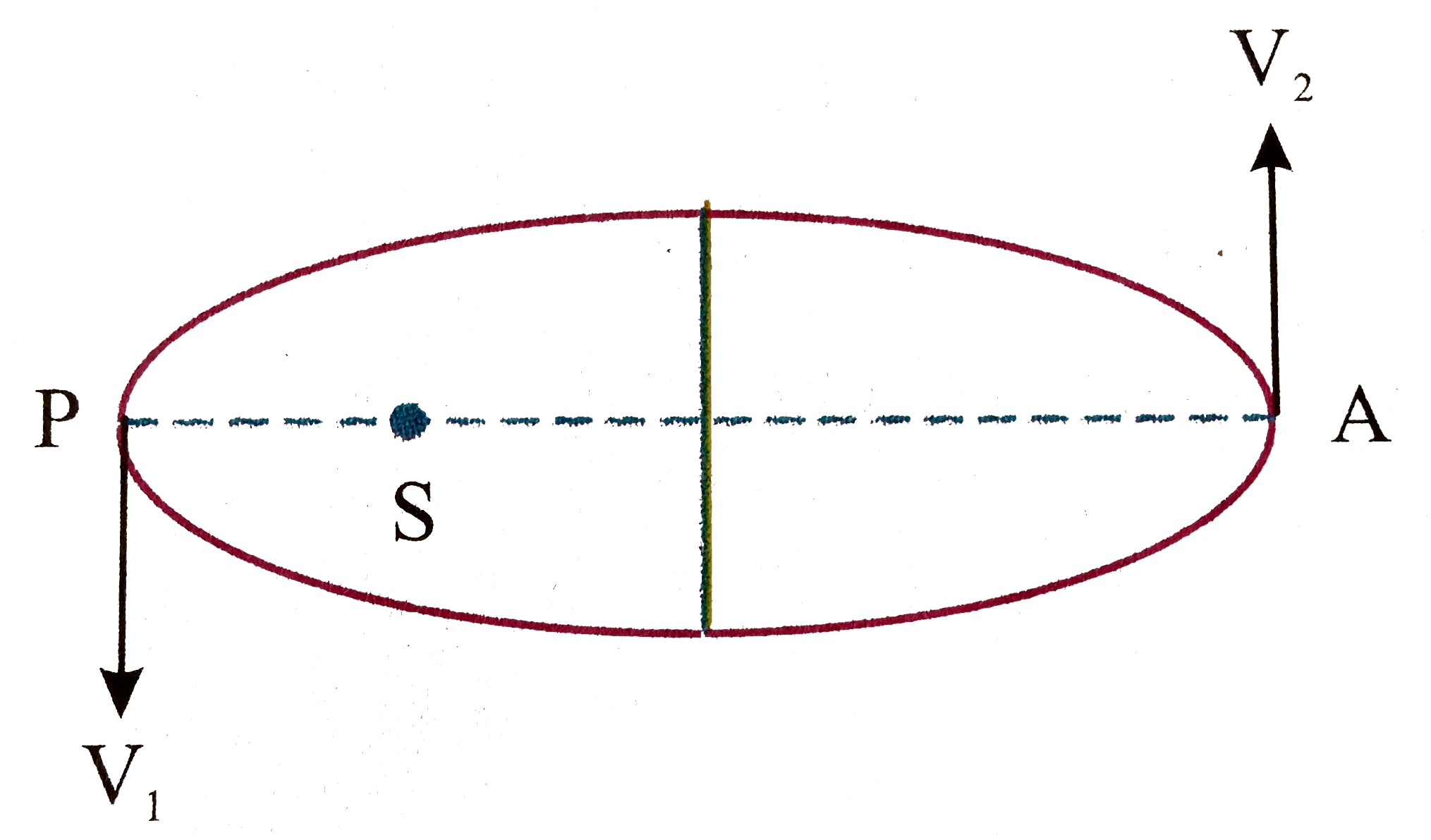
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.A√GMa(1+e)(1−e)B√GMa(1−e)(1+e)C√GMa3(1+e2)(1−e2)D√GMa3(1−e2)(1+e2)
A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
View SolutionWhich of the following statements are correct about a satellite moving around a planet in an elliptical orbit ?
View SolutionA planet of mass M is revolving round the sun in an elliptical orbit. If its angular momentum is J then the area swept per second by the line joining planet to sun will be :-
View SolutionA satellite of mass m moving around the earth of mass mE in a circular orbit of radius R has angular momentum L. The rate of the area swept by the line joining the centre of the earth and satellite is
View SolutionThe areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
View Solution
