To determine the half life of a radioactive element , a student plote a graph of in ∣∣∣dN(t)dt∣∣∣versust,Here∣∣∣dN(t)dt∣∣∣ is the rate of radioatuion decay at time t , if the number of radoactive nuclei of this element decreases by a factor of p after 4.16 year the value of p is

8
4
2
16
The correct Answer is:A
−dNdt=λN
⇒−dNdt=λN0e−λt
ln∣∣∣dNdt∣∣∣=−λt+ln(λN0)
y=mx+c⇒m=−λ ltbr gt λ=12 [Slope by graph =12]
T=ln2λ=2×0.693=4.16n
n=3 =no . of half life
p=z3=8.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.28
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.29
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.26
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
To determine the half life of a radioactive element , a student plot a graph of in ∣∣∣dN(t)dt∣∣∣ versus t , Here ∣∣∣dN(t)dt∣∣∣ is the rate of radiation decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after 4.16year the value of p is

View SolutionDraw a graph showing the variation of decay rate (−dNdt) with number (N) of radioactive nuclei.
View Solution
Knowledge Check
The graph between number of decayed atoms N' of a radioactive element and time t is.
A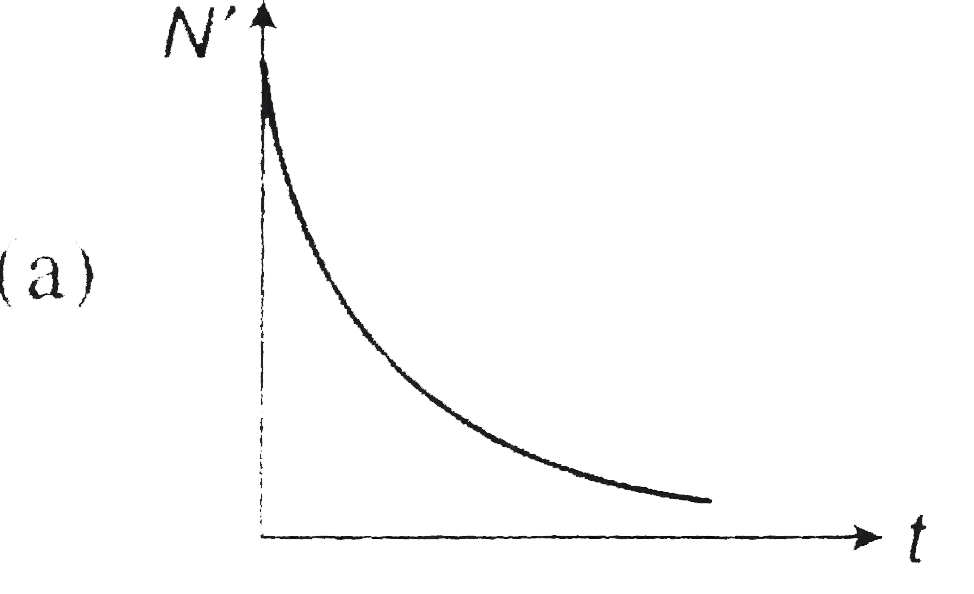 .B
.B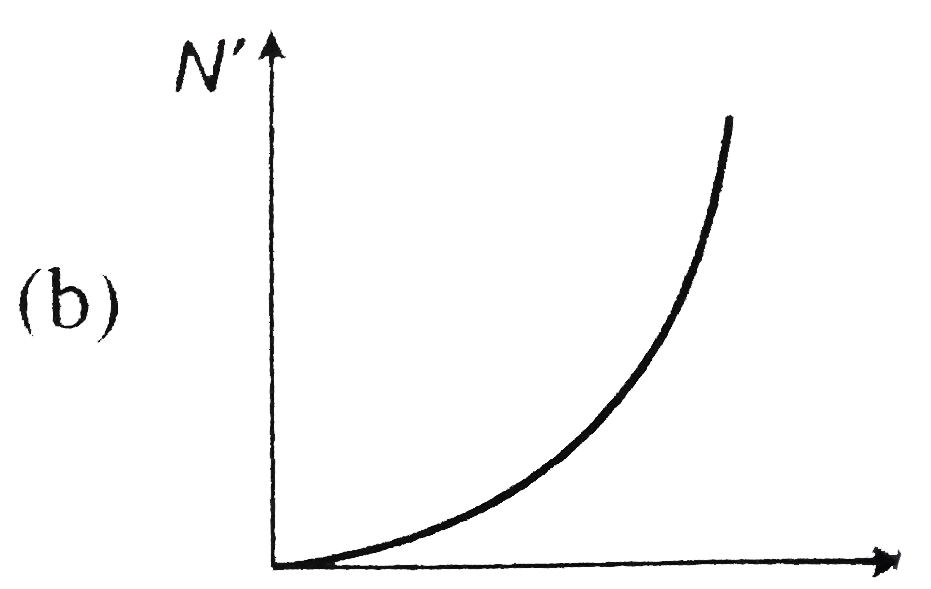 .C
.C .D
.D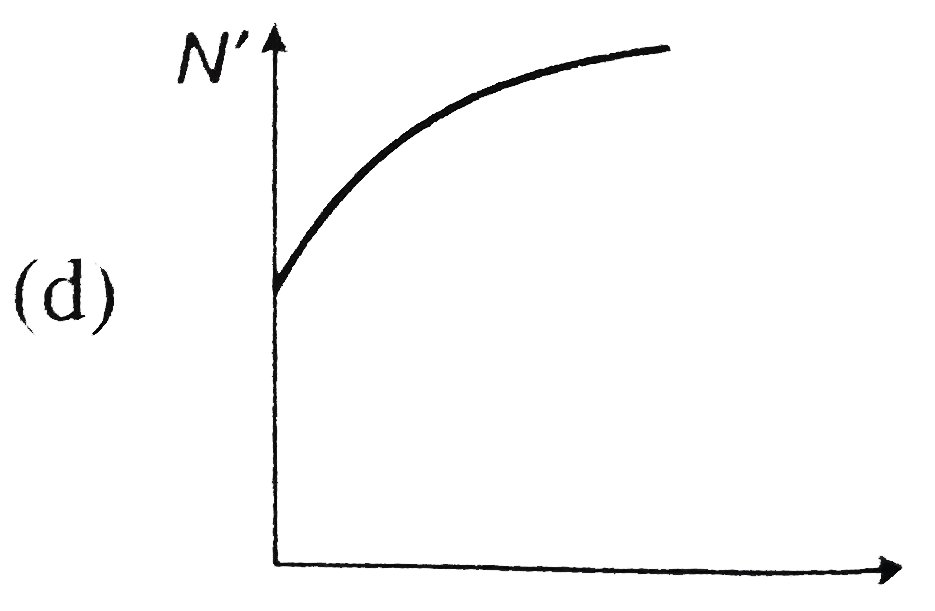 .
.The half-life period t1/2 of a radioactive element is N years. The period of its complete decays is
AN2 yearsB2N yearsC12N2 yearsDInfinityIf −(dNdt)o is the initial activity and −(dNdt) is the activity at time t in a radioactive disintegration then :
A−(dNdt)o=−(dNdt)e−ktB−(dNdt)o=(dNdt)oe−ktC−(dNdt)o=−(dNdt)oe−ktD−(dNdt)o=(dNdt)oe−kt
A radioactive sample decays to form a stable nuclide. A graph showing variation of rate of disintegration (dNdt) of radioactive sample with time (t) is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate α the element has a decay constant λ At time t=0 there are N0 nuclei of the element
The number of nuclei of A at time 't' is
View SolutionNuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ . At time t=0, there are N0 nuclei of the element . The number N of nuclei of A at time t is
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate, α . The element has a decay constant, λ. At time, t = 0, there are N0 nuclei of the element.
If α=2N0λ the number of nuclei of A after one half life of A becomes
View SolutionThe half life of a radioactive substance is 20 minutes. The approximate time interval (t2–t1) between the time t2 when 34 of it has decayed and time t1 when 14 of it had decayed is
View Solution
