A ball of mass 'm' drops from a height which sticks to a mass-less hanger after striking it. Neglecting overturning, Find out the maximum extension in rod, assuming that the rod is mass-less.
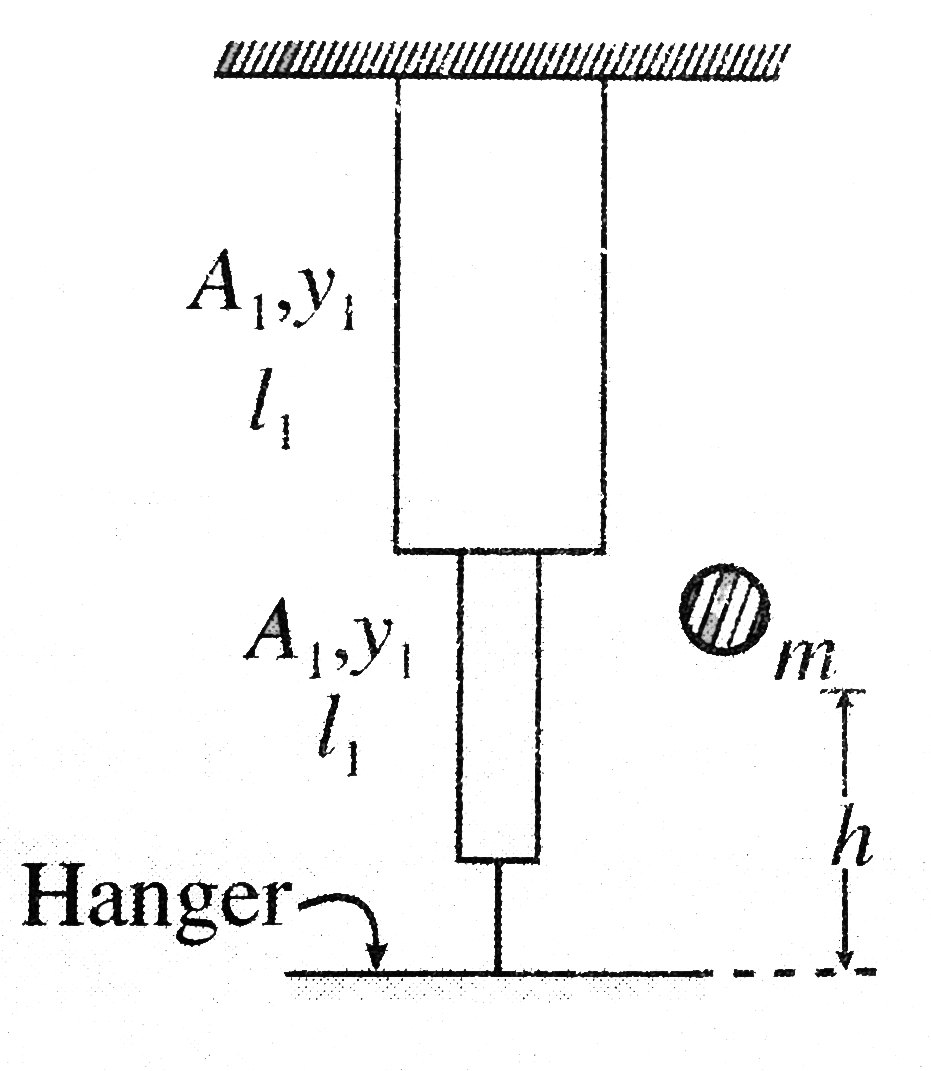
Applying energy conservation
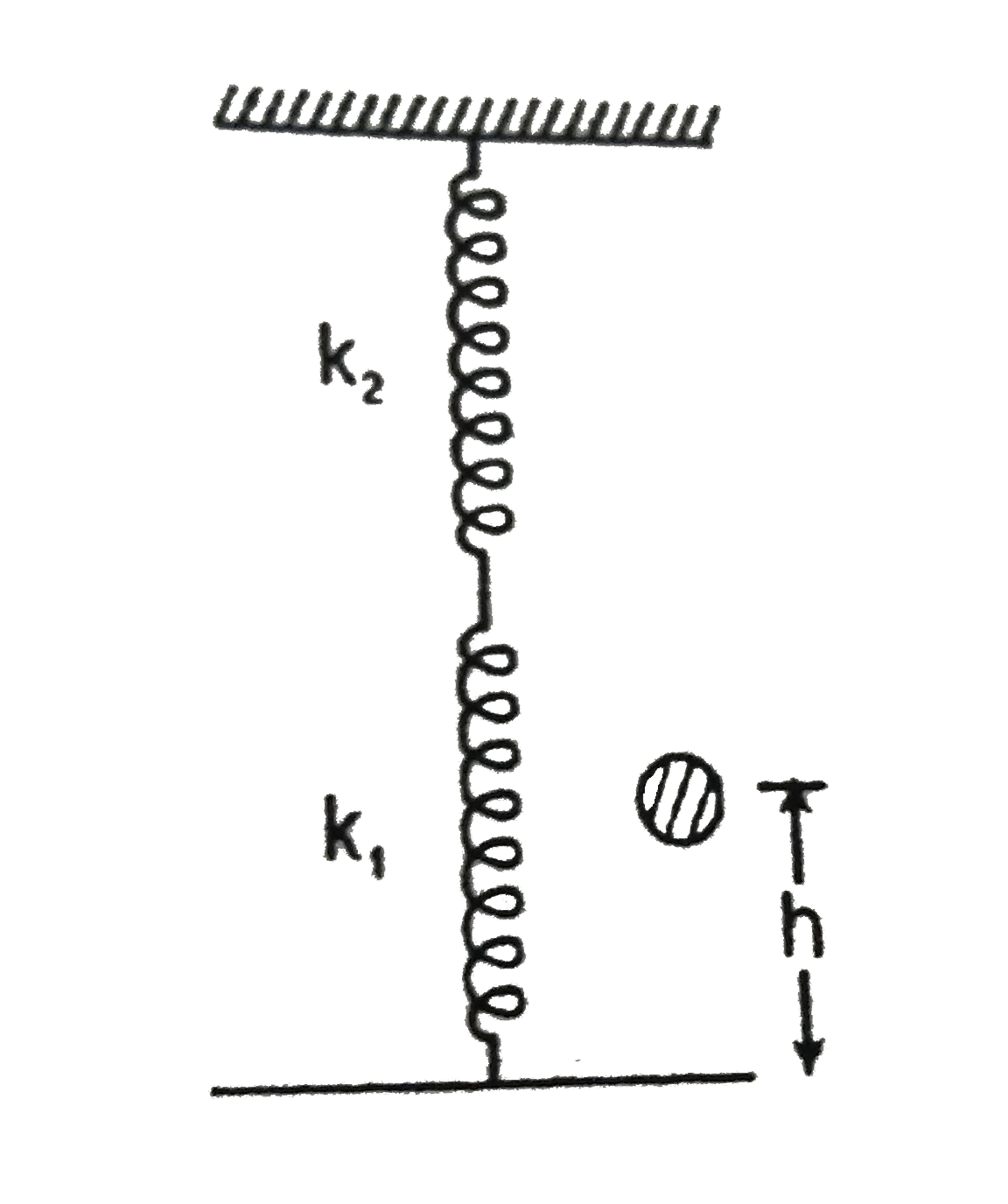
mg(h+x)=12k1k2k1+k2x2
where k1=A1y1l1k2=A2y2l2
&Keq=A1A2y1y2A1y1l2+A2y1l1
keqx2−2mgx−2mgh=0
x=2mg±√4m2g2+8mghkeq2keqxmax=mgkeq+√m2g2k2eq+2mghkeq
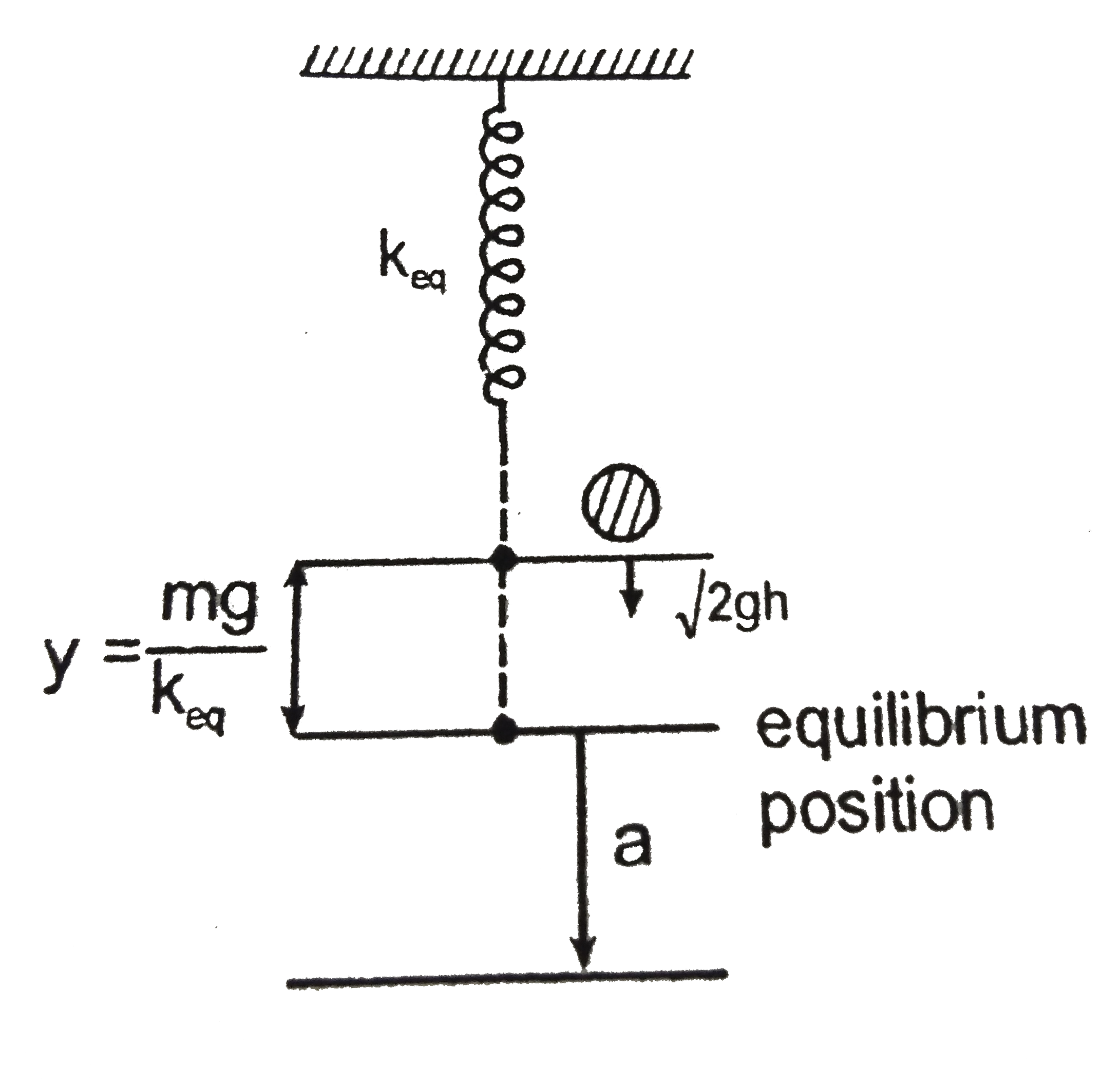
BY S.H.M.
w=√keqmv=ω√a2−y2
√2gh=√keqm√a2−y2⇒√2mghkeq+m2g2k2eq=a
mmax extension a+y=mgkeq+√m2g2keq+2mghkeq
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 91 illustration
2 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
View Solution_S01_010_Q01.png)
Hanger is mass less a ball of mass m drops a height h which sticks to hanger after striking. Neglect over turning find out the maximum extension in rod. Assuming or id massless let maximum extension be xmax.
View Solution
Knowledge Check
A ball of mass m is thrown straight up. It goes to a maximum height and then returns. Finally it strikes ground. In the whole process.
AThe momentum of the ball remains conservedBThe momentum of the earth remains conserved.CThe momentum of the ball and earth system remains conservedDnone of the above
A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
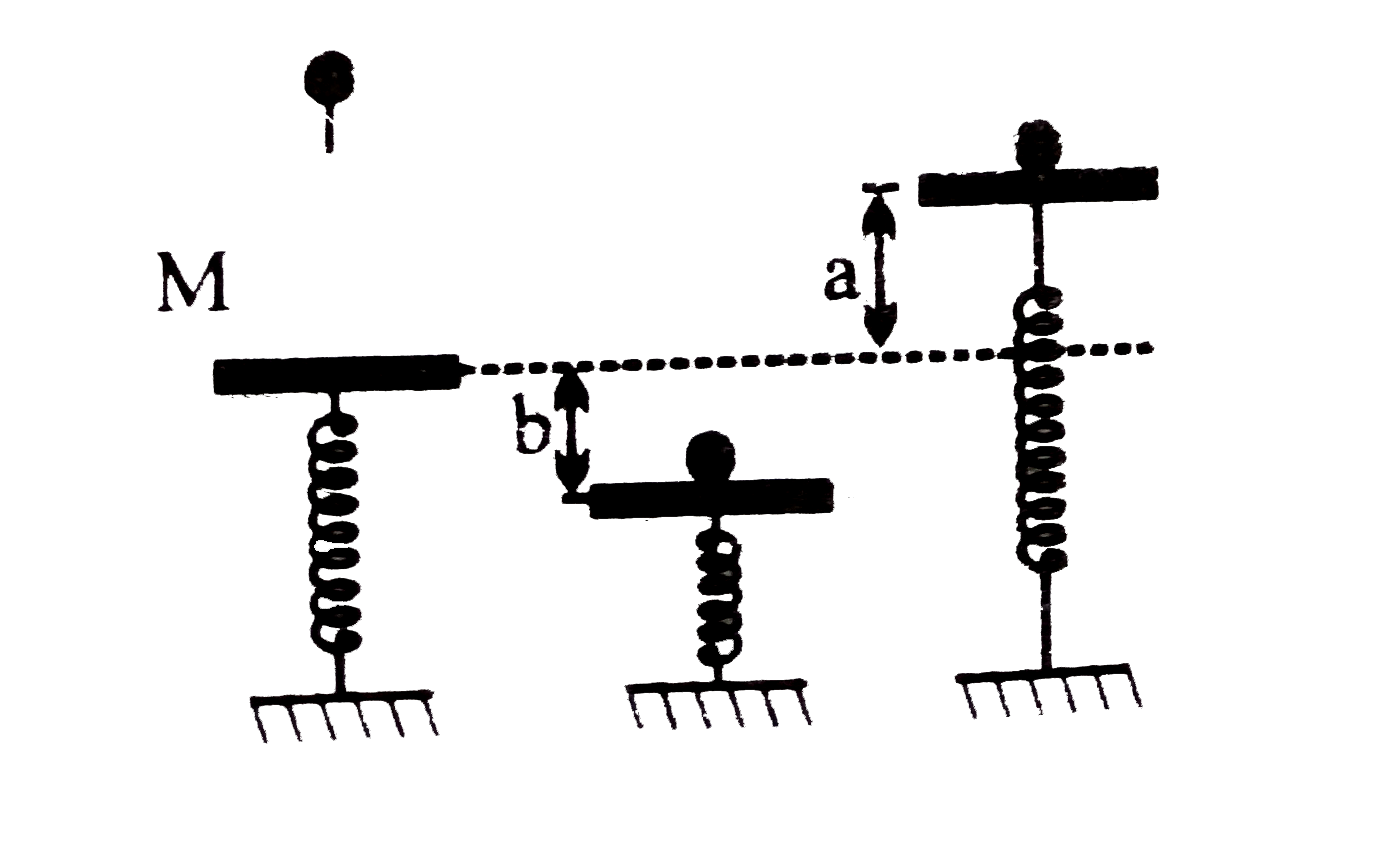
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.

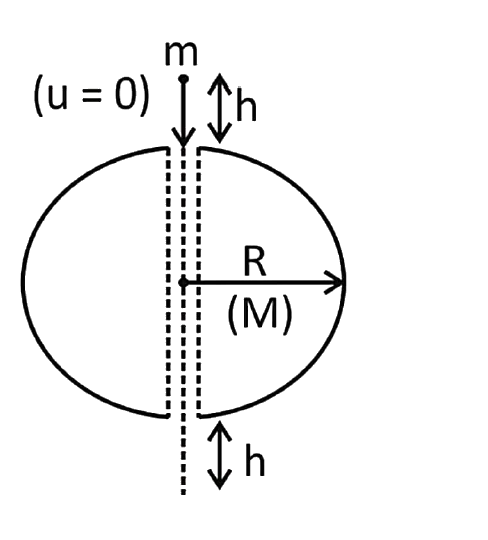
View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View SolutionA block of mass 200 gm is suspended through a vertical spring. The spring is stretched by 1 cm when the block is in equilibrium. A particle of mass 120 gm is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring.
View SolutionA block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
View SolutionA ball of mass 1kg is dropped from a height of 5m. (a) Find the kinetic of the ball just before it reaches the ground (b) What is the speed at this instant?
View Solution
