_S01_010_Q01.png)
Hanger is mass less a ball of mass m drops a height h which sticks to hanger after striking. Neglect over turning find out the maximum extension in rod. Assuming or id massless let maximum extension be xmax.
_S01_010_S01.png)
Applying energy conservation mg(h+xmax)=12k1k2k1+k2x2
where k1=A1y1l1,k2=A2y2l2&Keq=A1A2y1y2A1y1l2+A2y1l1
therefore keqx2max−2mgxmax−2mgh=0
xmax=2mg±√4m2g2+8mghkeq2keq=mgkeq+√m2g2k2eq+2mghkeq
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
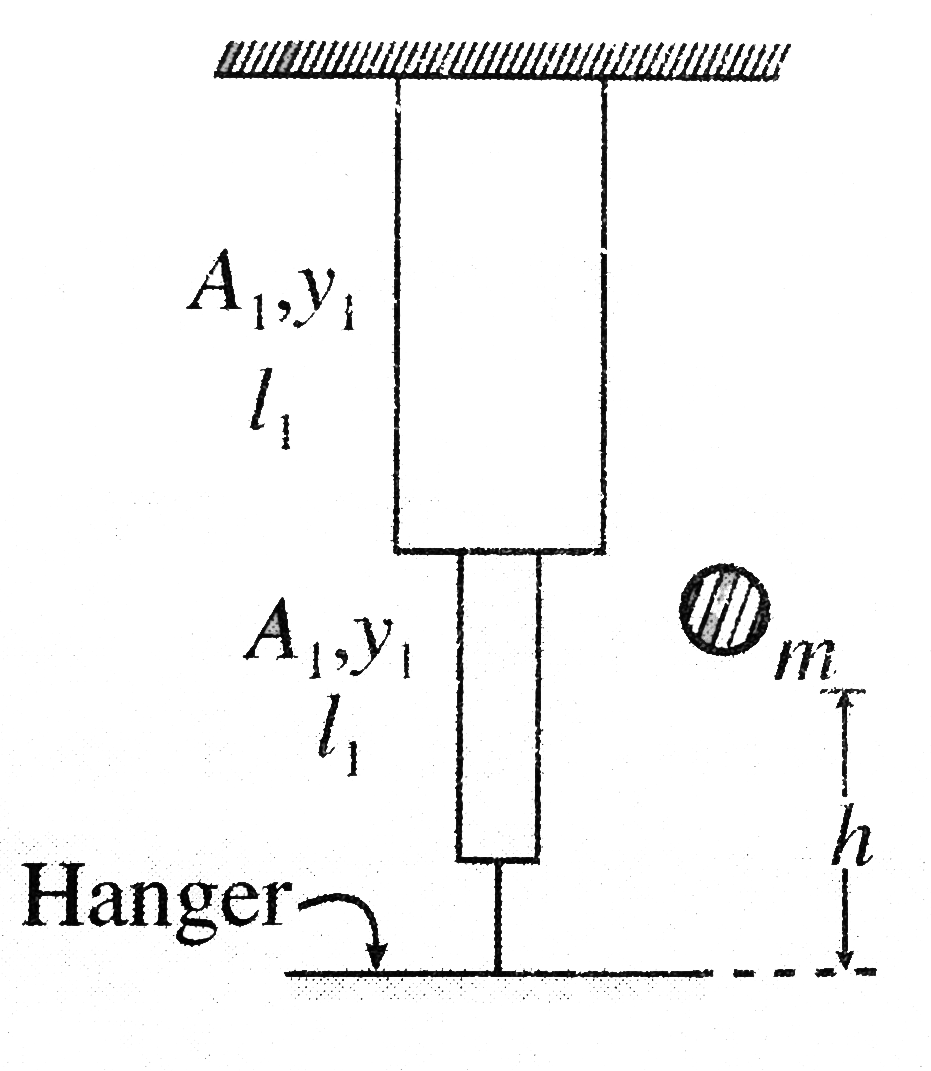
View SolutionA block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.
View Solution
Knowledge Check
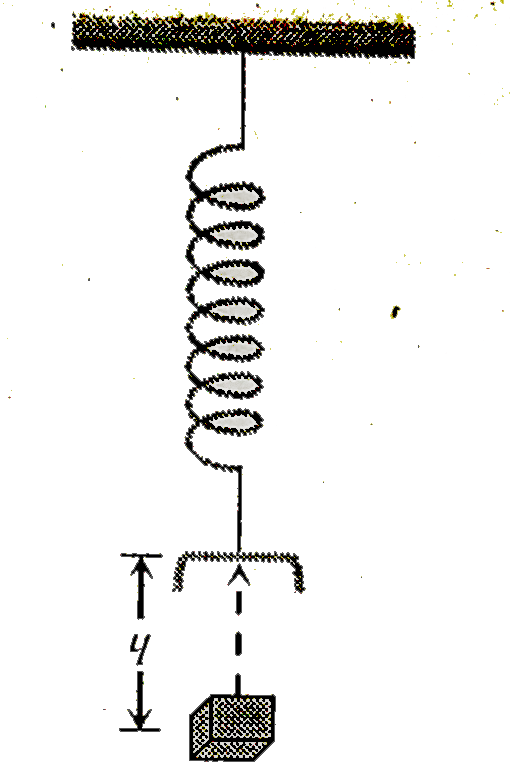
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2A block of mass m falls from a height h onto the end of a platform as shown in figure. The springis initially unstreched and the mass of the platform on be neglected. Assuming if there is no loss of energy, the maximum elongation of the spring is
 Amg+√m2g2+2mghKKBmg+√m2g2−2mghkKCK√m2g2+2mghkD√m2g2+2mghkK
Amg+√m2g2+2mghKKBmg+√m2g2−2mghkKCK√m2g2+2mghkD√m2g2+2mghkK

Consider the situation as shown. Initially the spring is unstretched when the block of mass m is released from rest assuming the pulley frictionless and light the spring and string massless. Find the extension of sprinig when the block is in equilibrium also find the maximum extension of the spring.
View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
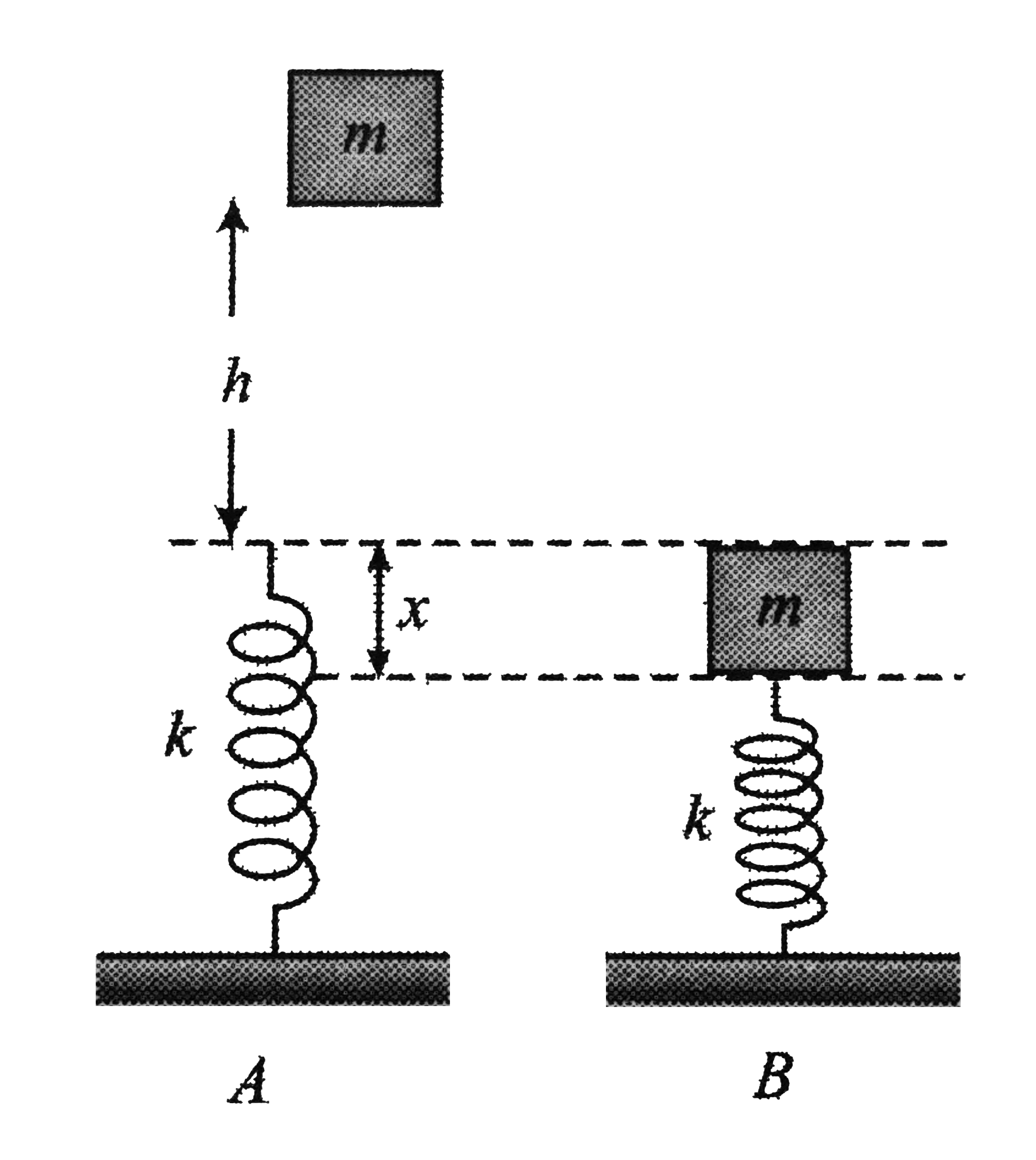
View SolutionIn the system shown in fig. block of mass M is placed on a smooth horizontal surface. There is a mass less rigid support attached to the block. Block of mass m is placed on the first block and it is connected to the support with a spring of force constant K. There is no friction between the blocks. A bullet of mass m0, moving with speed u hits the block of mass M and gets embedded into it. The collision is instantaneous. Assuming that m always stays over M, calculate the maximum extension in the spring caused during the subsequent motion.
K=8960N/m,u=400m/s
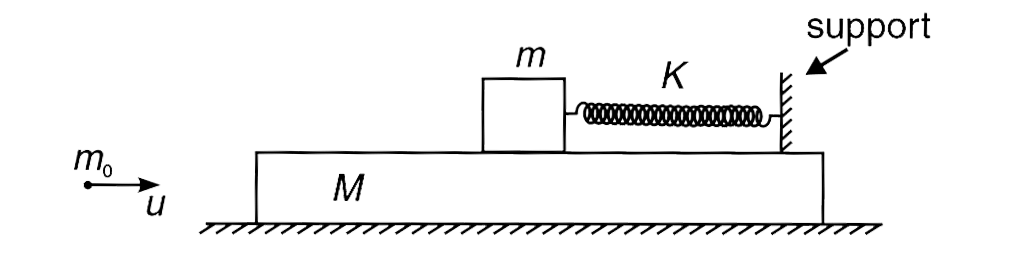
View SolutionIn the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
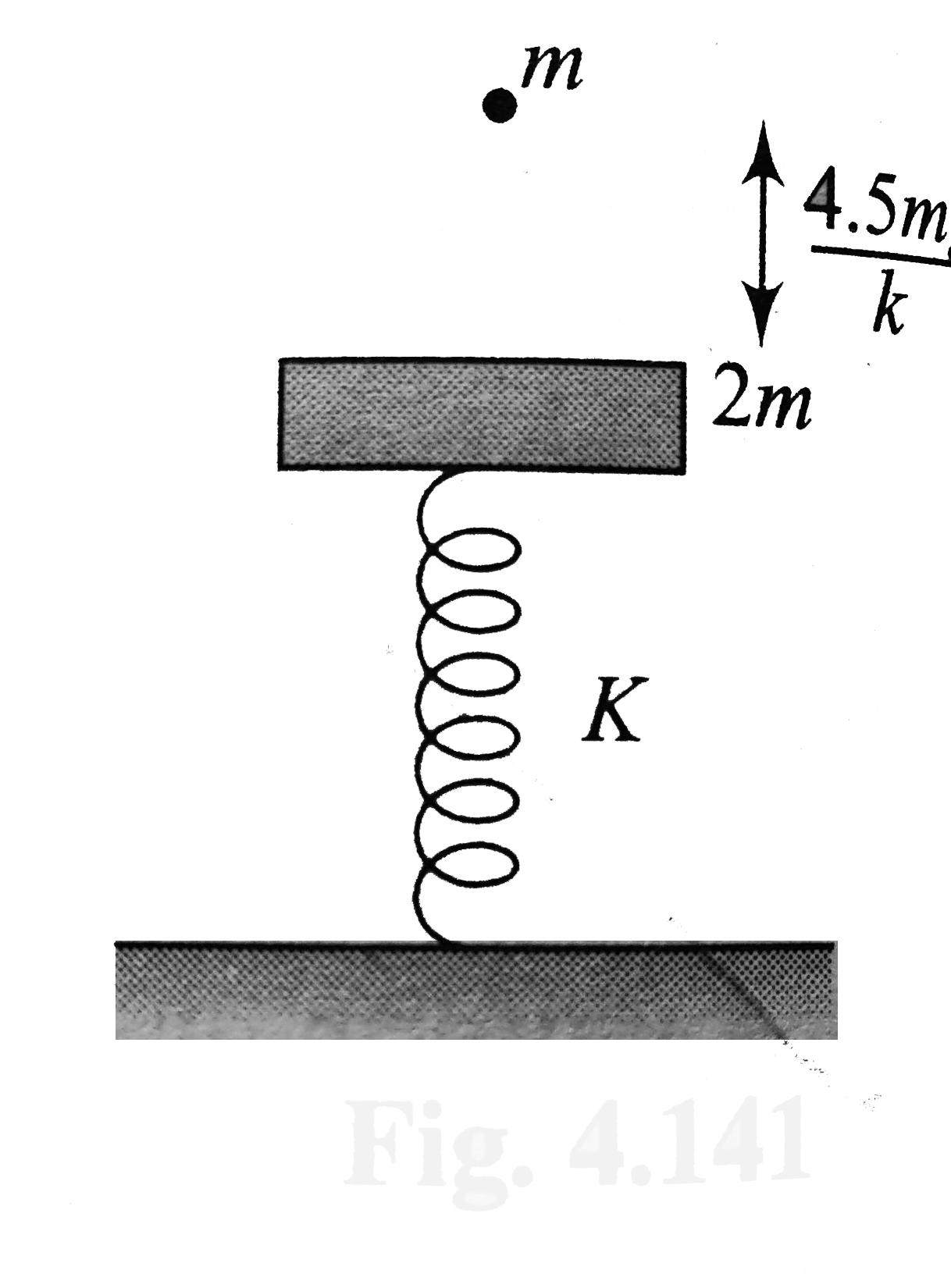
View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
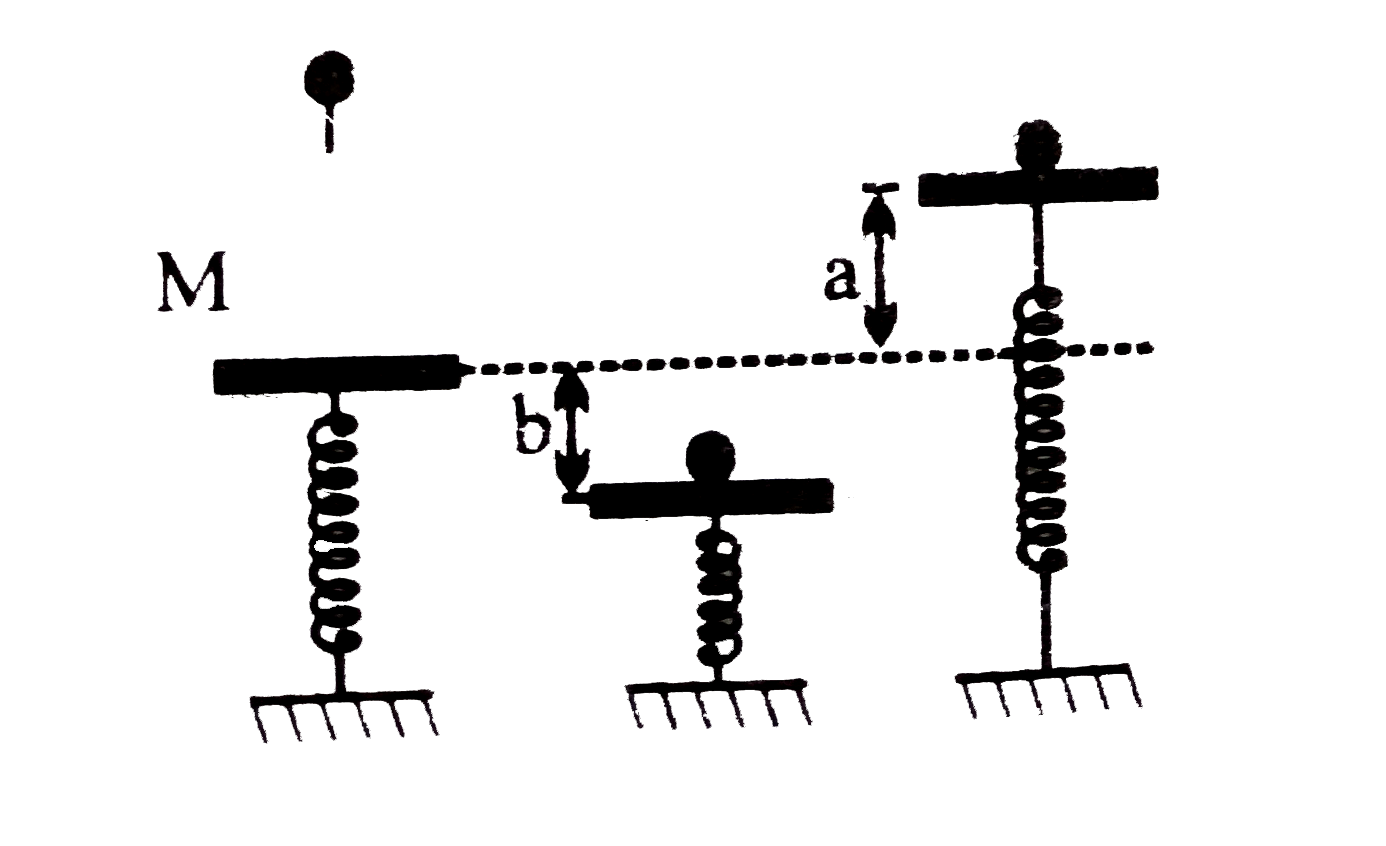
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA block of mass 180g is placed on a spring (spring constant k=120N/m) fixed from below. A ball of mass 20g is dropped from height 20m and the collision is completely inelastic. Find the maximum compression of the spring. Neglect the initial compression of the spring due to the block.
View Solution
