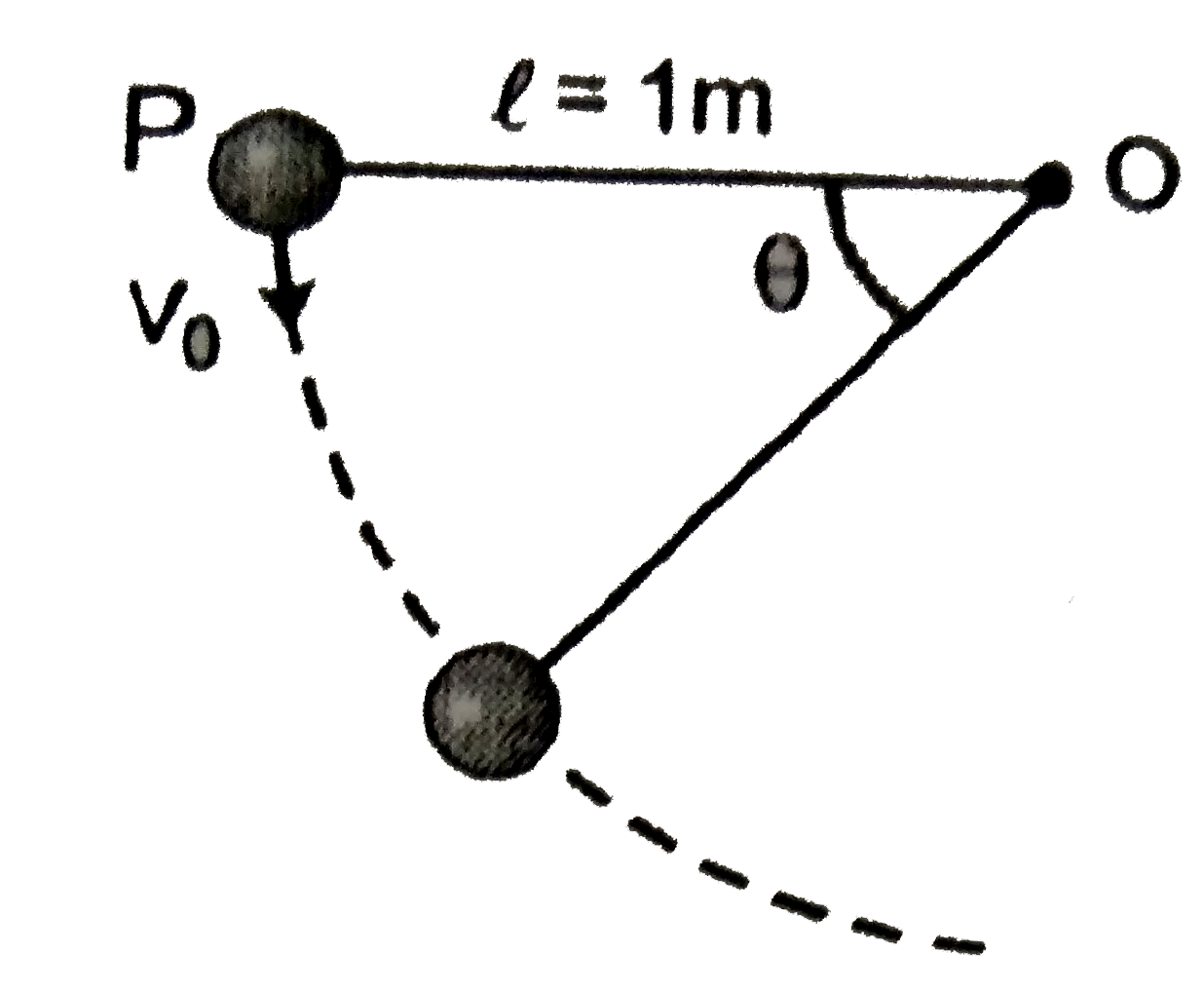
The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
g2m/s
2g3m/s
√3g2m/s
will have minimum value 38m
The correct Answer is:C
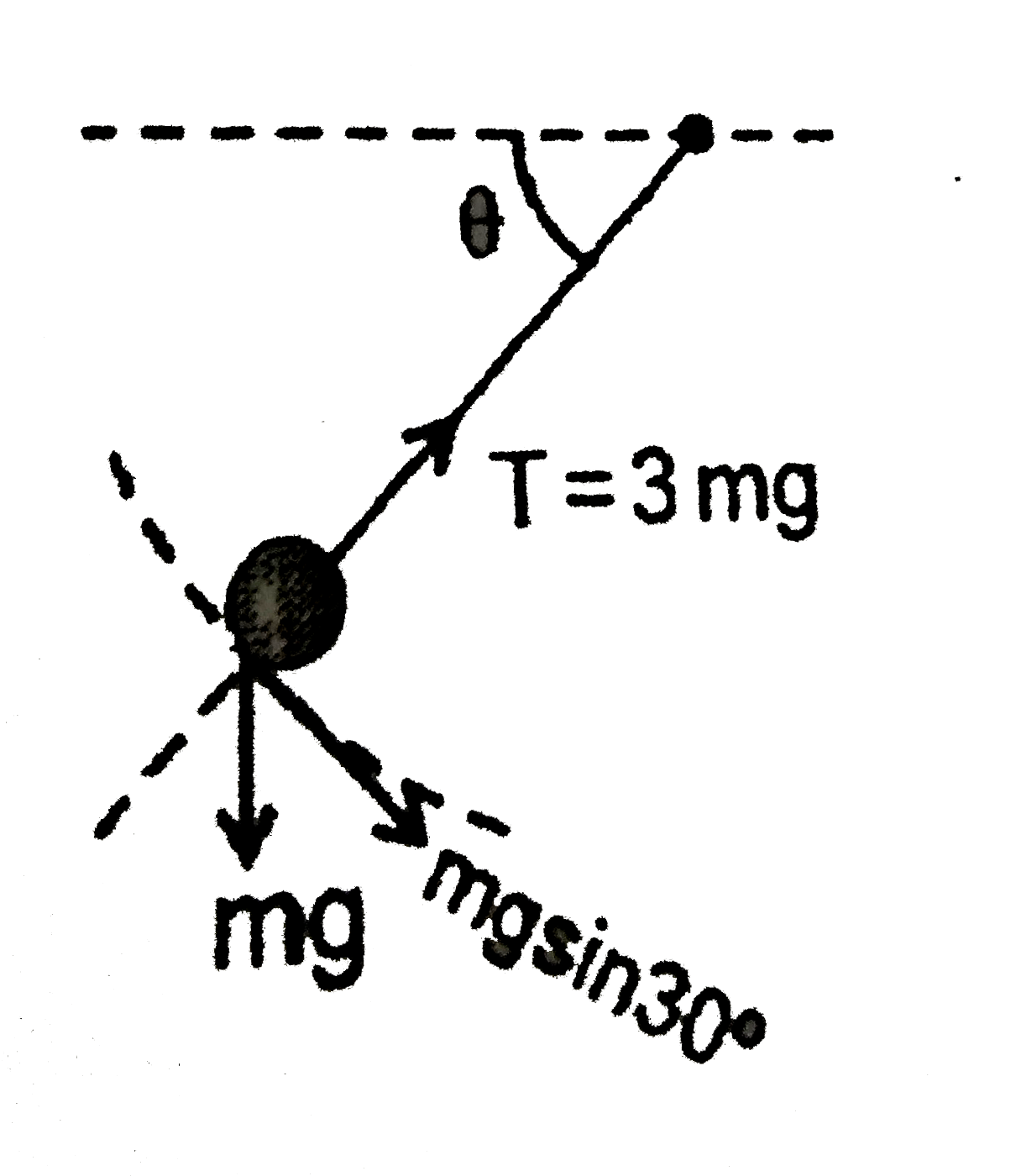
T=mgsinθ=mv2R
⇒3mg−mgsin30∘
=m.(u20+2glsin30∘)l
∴u0=√3g/2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 82
Explore 4 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 83
Explore 6 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 80
Explore 4 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
The sphere at P is given a down ward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal, knowing that it can withstand a maximum tension equal to four times the weight of the sphere. then the value of v0 will be (g=10m/s2).
 .
.
View SolutionThe sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
View Solution
Knowledge Check
A small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
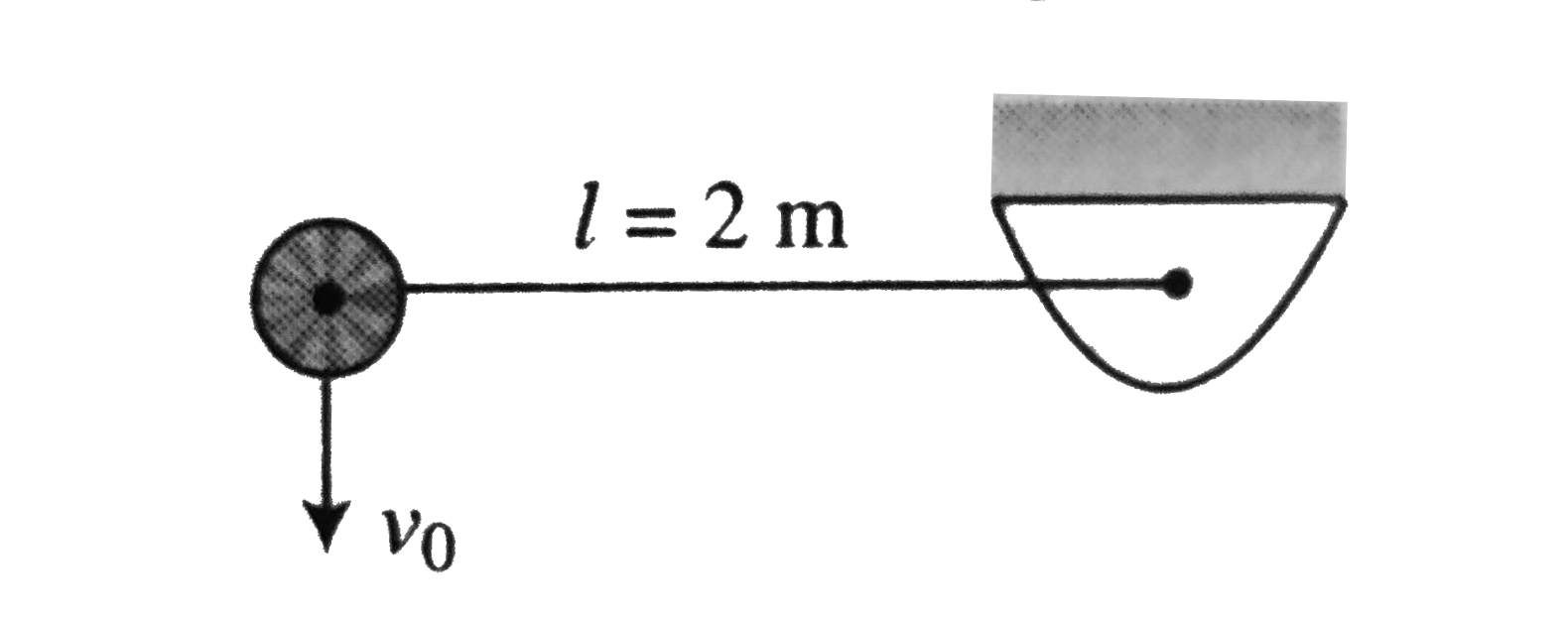 A(a) cos−123B(b) cos−1(14)C(c) 60∘D(d) 30∘
A(a) cos−123B(b) cos−1(14)C(c) 60∘D(d) 30∘A stone of mass 0.5 kg is attached to a string of length 2m and is whirled in a horizontal circle. If the string can withstand a tension of 9N, the maximum velocity with which the stone can be whirled is
A6ms−1B8ms−1C4ms−1D12ms−1A monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is:
(g=10m/s2)A2m/s2B3m/s2C4m/s2D5m/s2
A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
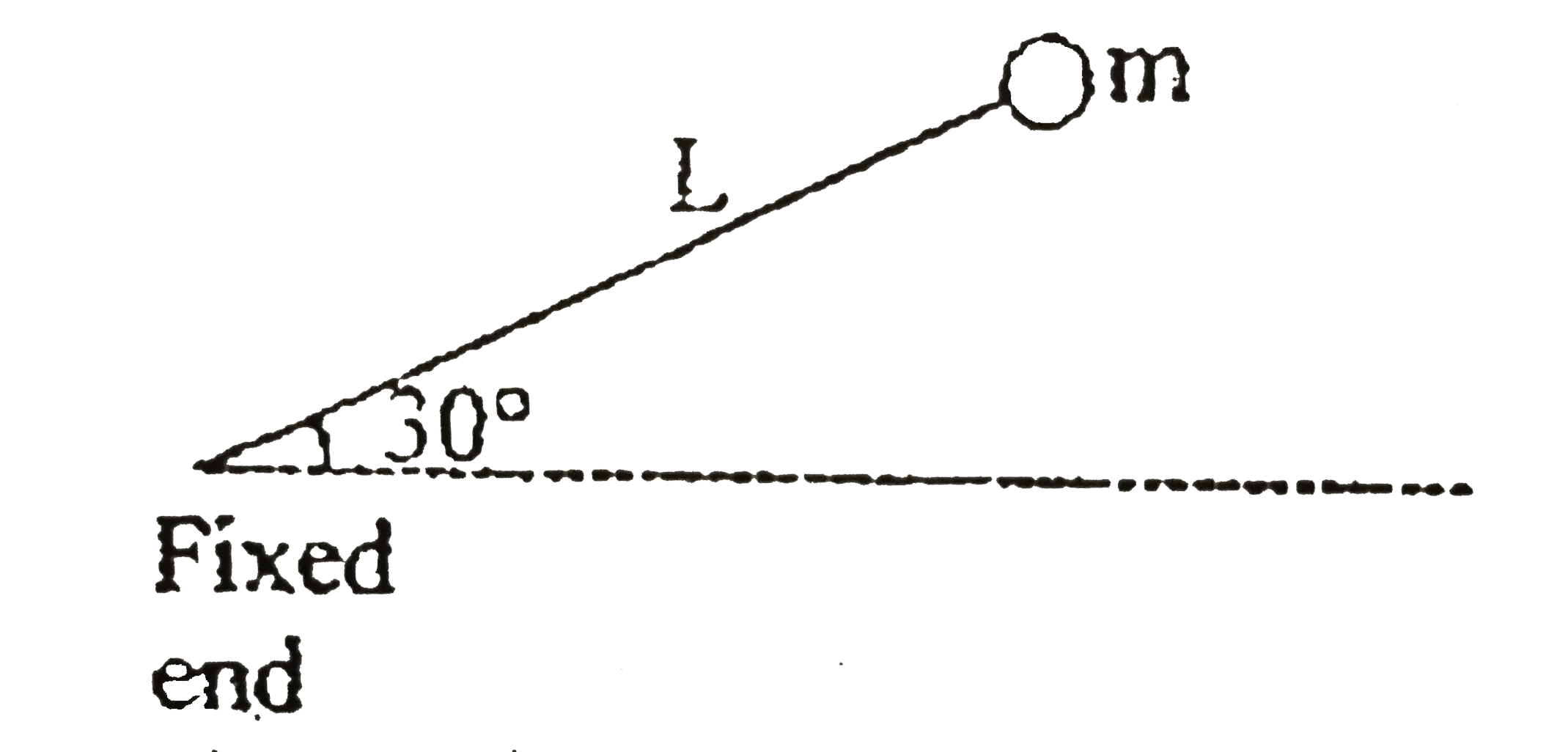
View SolutionA ball tied to a rope making an angle 30∘ with the horizontal is held so that the rope is just If the ball is released, calculate the heat generated in joule when it crosses 30∘ down the horizontal (dotted)Given m=Kg,L=2m,g=10m/s2.
View SolutionA bob tied to the end of a string of length 2m, other end of which is fixed at a point in a vertical wall at a point O. The bob is imparted a vertical downward velocity of 5m/s when the string is horizontal and swings in a vertical plane. Find the angular displacement of the bob from its initial position, when the string breaks. Given that the tensile strength of the string is twice the weight of the bob. Take g=10m/s2
View SolutionA body of mass 40 kg wants to climb up a rope hanging vertically. The rope can withstands a maximum tension of 500 N. What is the maximum acceleration with which the boy can climb rope? Tak e g=10m/s2
View SolutionA monkey of mass 40 kg climbs on a massless rope which can stand a maximum tension of 500 N. In which of the following cases will the rope break? (Take g=10ms−2)

View Solution

